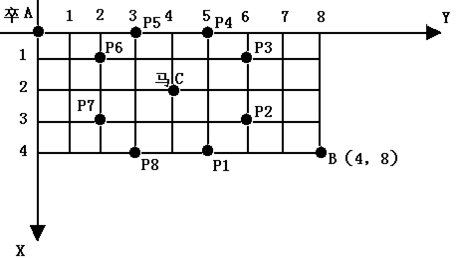
如图,A 点有一个过河卒,需要走到目标 B 点。卒行走规则:可以向下、或者向右。同时在棋盘上的任一点有一个对方的马(如上图的C点),该马所在的点和所有跳跃一步可达的点称为对方马的控制点。例如上图 C 点上的马可以控制 9 个点(图中的P1,P2 … P8 和 C)。卒不能通过对方马的控制点。
棋盘用坐标表示,A 点(0,0)、B 点(n,m)(n,m 为不超过 20 的整数,并由键盘输入),同样马的位置坐标是需要给出的(约定: C不等于A,同时C不等于B)。现在要求你计算出卒从 A 点能够到达 B 点的路径的条数。
1<=n,m<=15
键盘输入
B点的坐标(n,m)以及对方马的坐标(X,Y){不用判错}
屏幕输出
一个整数(路径的条数)。
6 6 3 2
17
题目分析:
要到达棋盘上的一个点,只能从左边过来(我们称之为左点)或是从上面过来(我们称之为上点),所以根据加法原理,到达某一点的路径数目,就等于到达其相邻的上点和左点的路径数目之和,因此我们可以使用逐列(或逐行)递推的方法来求出从起点到终点的路径数目。障碍点(马的控制点)也完全适用,只要将到达该点的路径数目设置为0即可。
用F[i][j]表示到达点(i,j)的路径数目,g[i][j]表示点(i, j)有无障碍,g[i][j]=0表示无障碍,g[i][j]=1表示有障碍。
则,递推关系式如下: F[i][j] = F[i-1][j] + F[i][j-1] //i>0且j>0且g[i][j]= 0
递推边界有4个:
F[i][j] = 0 //g[i][j] = 1
F[i][0] = F[i-1][0] //i > 0且g[i][0] = 0
F[0][j] = F[0][j-1] //j > 0且g[0][j] = 0
F[0][0] = 1
考虑到最大情况下:n=20,m=20,路径条数可能会超过231-1,所以要用高精度。
1 #include <stdio.h> 2 int main(int argc, char *argv[]) 3 { 4 int F[21][21]={0},G[21][21]={0}; 5 int i,j; 6 int n,m;//终点坐标 7 int a,b;//马的坐标 8 9 scanf("%d%d",&n,&m);//输入终点坐标 10 scanf("%d%d",&a,&b);//输入马的坐标 11 12 G[a][b]=1; 13 if(a-2>=0&&b-1>=0) {G[a-2][b-1]=1;} 14 if(a-2>=0&&b+1<=m) {G[a-2][b+1]=1;} 15 if(a+2<=n&&b-1>=0) {G[a+2][b-1]=1;} 16 if(a+2<=n&&b+1<=m) {G[a+2][b+1]=1;} 17 18 if(a-1>=0&&b-2>=0) {G[a-1][b-2]=1;} 19 if(a-1>=0&&b+2<=m) {G[a-1][b+2]=1;} 20 if(a+1<=n&&b-2>=0) {G[a+1][b-2]=1;} 21 if(a+1<=n&&b+2<=m) {G[a+1][b+2]=1;} 22 23 for(i=0;i<=n;i++)//初始化第一行和第一列,均为1种走法。 24 { 25 if(G[i][0]==0){F[i][0]=1;} 26 else break; 27 } 28 for(i=0;i<=m;i++) 29 { 30 if(G[0][i]==0) {F[0][i]=1;} 31 else break; 32 } 33 for(i=1;i<=m;i++) 34 { 35 for(j=1;j<=n;j++) 36 { 37 if(G[j][i]!=1) 38 { 39 F[j][i]=F[j-1][i]+F[j][i-1]; 40 } 41 } 42 } 43 printf("%d",F[n][m]); 44 45 return 0; 46 }
另一段比较优秀的代码:
1 #include <stdio.h> 2 #include <stdlib.h> 3 int detX[8]={2,1,-1,-2,-2,-1,+1,+2}; 4 int detY[8]={1,2,+2,+1,-1,-2,-2,-1}; 5 int main() 6 { 7 int n,m,x,y,i,j; 8 long long F[25][25]={0}; 9 int xx,yy; 10 scanf("%d%d%d%d",&n,&m,&x,&y); 11 12 F[x][y]=-1; 13 for(i=0;i<8;i++) 14 { 15 xx=x+detX[i]; yy=y+detY[i]; 16 if(xx>=0&&xx<=n&&yy>=0&&yy<=m) F[xx][yy]=-1; 17 } 18 19 F[0][0]=1; 20 for(i=1;i<=n;i++)//初始化第0列 21 { 22 if(F[i][0]!=-1) F[i][0]=F[i-1][0]; 23 else F[i][0]=0; 24 } 25 for(j=1;j<=m;j++)//初始化第0行 26 { 27 if(F[0][j]!=-1) F[0][j]=F[0][j-1]; 28 else F[0][j]=0; 29 } 30 31 for(i=1;i<=n;i++) 32 { 33 for(j=1;j<=m;j++) 34 { 35 if(F[i][j]!=-1) F[i][j]=F[i][j-1]+F[i-1][j]; 36 else F[i][j]=0; 37 } 38 } 39 printf("%lld ",F[n][m]); 40 return 0; 41 }