一、图的常用概念
1、顶点(vertex)
2、边(edge)
3、路径
4、无向图:顶点之间的连接没有方向
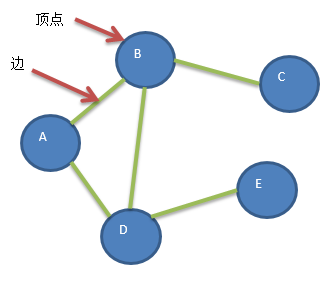
5、有向图:有方向
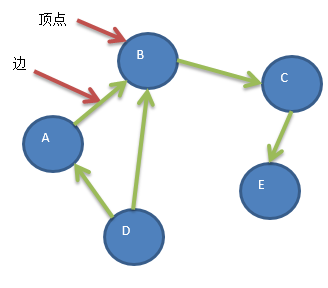
6、带全图
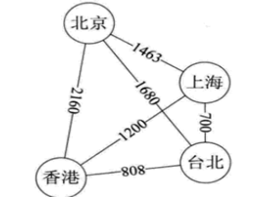
二、图的表示方式
图的表示方式有两种:二维数组(邻接矩阵),链表(邻接表)
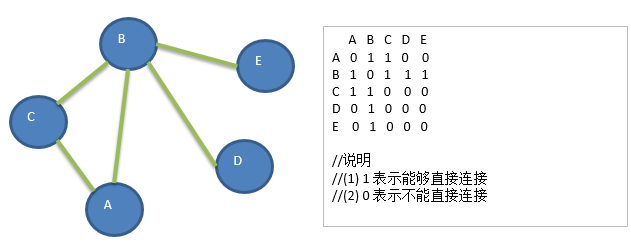
1、邻接矩阵
邻接矩阵是表示图形中顶点之间相邻关系的矩阵,对于n个顶点的图而言,矩阵的row和col表示的是1-n个点
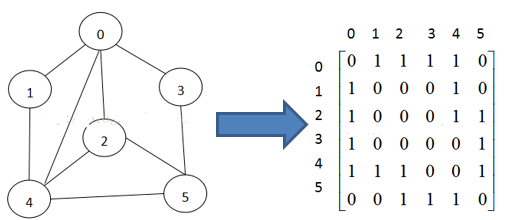
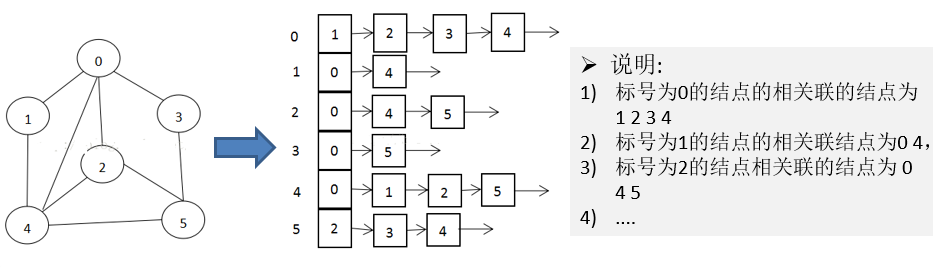
2、邻接表
邻接矩阵需要为每个顶点都分配n个边的空间,其实很多边都是不存在,会造成空间的浪费
邻接表的实现只关心存在的边,不关心不存在的边。因此没有浪费空间,邻接表由数组+链表组成
三、深度优先遍历(Depth First Search)
深度优先遍历基本思想:
- 深度优先遍历,从初始访问结点出发,初始访问结点可能有多个邻接结点,深度优先遍历的策略就是首先访问第一个邻接结点,然后再以这个被访问的邻接结点作为初始结点,访问它的第一个邻接结点, 可以这样理解:每次都在访问完当前结点后首先访问当前结点的第一个邻接结点。
- 我们可以看到,这样的访问策略是优先往纵向挖掘深入,而不是对一个结点的所有邻接结点进行横向访问。
- 显然,深度优先搜索是一个递归的过程
深度优先遍历步骤:
- 访问初始结点v,并标记结点v为已访问。
- 查找结点v的第一个邻接结点w。
- 若w存在,则继续执行4,如果w不存在,则回到第1步,将从v的下一个结点继续。
- 若w未被访问,对w进行深度优先遍历递归(即把w当做另一个v,然后进行步骤123)。
- 查找结点v的w邻接结点的下一个邻接结点,转到步骤3
代码实现:
1 private void dfs() { 2 isVisited = new boolean[vertexList.size()]; 3 for (int i = 0; i < vertexList.size(); i++) { 4 if (!isVisited[i]){ 5 dfs(isVisited,i); 6 } 7 } 8 } 9 //深度优先遍历算法 10 //i 第一次就是 0 11 private void dfs(boolean[] isVisited, int i) { 12 //输出,访问的结点 13 System.out.println(vertexList.get(i)+"->"); 14 //将结点设置为已访问过 15 isVisited[i] = true; 16 //查找结点i的第一个领结节点w 17 int w = getFirstNeighbor(i); 18 while (w!=-1){ 19 if (!isVisited[w]){ 20 dfs(isVisited,w); 21 } 22 //如果w结点已经被访问过 23 w=getNextNeighbor(i,w); 24 } 25 }
四、广度优先遍历(Broad First Search)
广度优先遍历基本思想:
类似于一个分层搜索的过程,广度优先遍历需要使用一个队列以保持访问过的结点的顺序,以便按这个顺序来访问这些结点的邻接结点
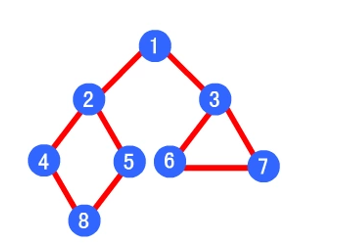
深度优先遍历顺序为 1->2->4->8->5->3->6->7
广度优先算法的遍历顺序为:1->2->3->4->5->6->7->8
广度优先遍历步骤:
- 访问初始结点v并标记结点v为已访问。
- 结点v入队列
- 当队列非空时,继续执行,否则算法结束。
- 出队列,取得队头结点u。
- 查找结点u的第一个邻接结点w。
- 若结点u的邻接结点w不存在,则转到步骤3;否则循环执行以下三个步骤:
6.1 若结点w尚未被访问,则访问结点w并标记为已访问。
6.2 结点w入队列
6.3 查找结点u的继w邻接结点后的下一个邻接结点w,转到步骤6。
代码:
1 private void bfs() { 2 isVisited = new boolean[vertexList.size()]; 3 for (int i = 0; i < vertexList.size(); i++) { 4 if (!isVisited[i]){ 5 bfs(isVisited,i); 6 } 7 } 8 } 9 10 private void bfs(boolean[] isVisited, int i) { 11 int u;//表示队列的头结点对应下标 12 int w;//邻接节点w 13 14 //记录节点的访问顺序 15 LinkedList queue = new LinkedList(); 16 System.out.println(vertexList.get(i)+"=>"); 17 isVisited[i] = true; 18 queue.addLast(i); 19 20 while (!queue.isEmpty()){ 21 //取出队列的头结点下标 22 u= (int) queue.removeFirst(); 23 //得到第一个邻接点的下标w 24 w=getFirstNeighbor(u); 25 while (w!=-1){//找到 26 if(!isVisited[w]){ 27 System.out.println(vertexList.get(w)+"=>"); 28 isVisited[w] = true; 29 queue.addLast(w); 30 } 31 //以u为前驱点,找w后面的下一个邻接点 32 w=getNextNeighbor(u,w); 33 } 34 } 35 }
五、完整代码
1 public class Graph { 2 3 //存储顶点集合 4 private ArrayList<String> vertexList; 5 //存储图对应的邻接矩阵 6 private int[][] edges; 7 //表示边的数目 8 private int numOfEdges; 9 //定义给数组boolean【】,记录某个结点是否被访问过 10 private boolean[] isVisited; 11 12 public Graph(int n) { 13 edges = new int[n][n]; 14 vertexList = new ArrayList<>(n); 15 numOfEdges = 0; 16 } 17 18 public static void main(String[] args) { 19 20 int n = 5;//结点个数 21 // String vertexs[] = {"1", "2", "3", "4", "5", "6", "7", "8"}; 22 String vertexs[] = {"A", "B", "C", "D", "E"}; 23 //创建图对象 24 Graph graph = new Graph(n); 25 for (String vertex : vertexs) { 26 graph.insertVertex(vertex); 27 } 28 //更新边的关系 29 // graph.insertEdge(0, 1, 1); 30 // graph.insertEdge(0, 2, 1); 31 // graph.insertEdge(1, 3, 1); 32 // graph.insertEdge(1, 4, 1); 33 // graph.insertEdge(3, 7, 1); 34 // graph.insertEdge(4, 7, 1); 35 // graph.insertEdge(2, 5, 1); 36 // graph.insertEdge(2, 6, 1); 37 // graph.insertEdge(5, 6, 1); 38 graph.insertEdge(0, 1, 1); 39 graph.insertEdge(0, 2, 1); 40 graph.insertEdge(1, 3, 1); 41 graph.insertEdge(1, 2, 1); 42 graph.insertEdge(1, 4, 1); 43 graph.showGraph(); 44 45 System.out.println("深度遍历"); 46 graph.dfs(); 47 System.out.println("广度优先"); 48 graph.bfs(); 49 } 50 51 private void dfs() { 52 isVisited = new boolean[vertexList.size()]; 53 for (int i = 0; i < vertexList.size(); i++) { 54 if (!isVisited[i]){ 55 dfs(isVisited,i); 56 } 57 } 58 } 59 //深度优先遍历算法 60 //i 第一次就是 0 61 private void dfs(boolean[] isVisited, int i) { 62 //输出,访问的结点 63 System.out.println(vertexList.get(i)+"->"); 64 //将结点设置为已访问过 65 isVisited[i] = true; 66 //查找结点i的第一个领结节点w 67 int w = getFirstNeighbor(i); 68 while (w!=-1){ 69 if (!isVisited[w]){ 70 dfs(isVisited,w); 71 } 72 //如果w结点已经被访问过 73 w=getNextNeighbor(i,w); 74 } 75 } 76 77 //得到第一个邻接节点的下标w 78 //如果存在就返回对应的下标,否则返回-1 79 private int getFirstNeighbor(int i) { 80 for (int j = 0; j < vertexList.size(); j++) { 81 if (edges[i][j]>0){ 82 return j; 83 } 84 } 85 return -1; 86 } 87 //根据前一个邻接结点的下标来获取下一个邻接结点 88 public int getNextNeighbor(int v1, int v2) { 89 for (int i = v2+1; i < vertexList.size(); i++) { 90 if (edges[v1][i]>0){ 91 return i; 92 } 93 } 94 return -1; 95 } 96 97 98 private void bfs() { 99 isVisited = new boolean[vertexList.size()]; 100 for (int i = 0; i < vertexList.size(); i++) { 101 if (!isVisited[i]){ 102 bfs(isVisited,i); 103 } 104 } 105 } 106 107 private void bfs(boolean[] isVisited, int i) { 108 int u;//表示队列的头结点对应下标 109 int w;//邻接节点w 110 111 //记录节点的访问顺序 112 LinkedList queue = new LinkedList(); 113 System.out.println(vertexList.get(i)+"=>"); 114 isVisited[i] = true; 115 queue.addLast(i); 116 117 while (!queue.isEmpty()){ 118 //取出队列的头结点下标 119 u= (int) queue.removeFirst(); 120 //得到第一个邻接点的下标w 121 w=getFirstNeighbor(u); 122 while (w!=-1){//找到 123 if(!isVisited[w]){ 124 System.out.println(vertexList.get(w)+"=>"); 125 isVisited[w] = true; 126 queue.addLast(w); 127 } 128 //以u为前驱点,找w后面的下一个邻接点 129 w=getNextNeighbor(u,w); 130 } 131 } 132 } 133 134 //显示图对应的矩阵 135 public void showGraph() { 136 for (int[] link : edges) { 137 System.out.println(Arrays.toString(link)); 138 } 139 } 140 141 /** 142 * @param v1 表示点的下标即使第几个顶点 "A"-"B" "A"->0 "B"->1 143 * @param v2 第二个顶点对应的下标 144 * @param weight 表示 145 */ 146 private void insertEdge(int v1, int v2, int weight) { 147 edges[v1][v2] = weight; 148 edges[v2][v1] = weight; 149 numOfEdges++; 150 } 151 152 private void insertVertex(String vertex) { 153 vertexList.add(vertex); 154 } 155 }