首先考虑下面的阶乘函数:
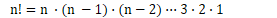

然后注意到1!等于1,就可以翻译出如下的代码:
int factorial(int n) { if(n == 1) { return 1; } return n * factorial(n -1); }
多么的简洁明了,对于factorial(4)可以写出下面的递归过程
factorial(4)
4*factorial(3)
4*3*factorial(2)
4*3*2*factorial(1)
4*3*2*1
4*3*2
4*6
24
下面换一种思路计算阶乘,可以将计算阶乘n!的规则描述为:
先将1和2相乘,结果保存起来计为product,再和3相乘,然后一直乘到n。可以看出这里面包含一个
从1到n的计数器counter
这一计算过程可以描述如下:
Counter *product -> product
Counter + 1 -> counter
n!也就是计数器counter超过n时乘积product的值。
可以描述为下面的代码:
int fact(int n) { return fact_iter(1, 1, n); } int fact_iter(int product, int cnt, int max_cnt) { if(cnt > max_cnt) { return product; } return fact_iter(cnt*product, cnt + 1, max_cnt); }
对于fact(4)可以写出下面的迭代过程
fact (4)
fact_iter (1, 1, 4)
fact_iter (1, 2, 4)
fact_iter (2, 3, 4)
fact_iter (6, 4, 4)
fact_iter (24, 5, 4)
24
现在来对两个计算过程做一个比较,从运算的步骤来看,两种所需要的步骤数目都是正比于n的,但从另一方面,如果我们考虑两个计算过程的"形状"就会发现他们的进展情况就会大不一样!
在第一个计算过程的"形状"呈先逐步展开而后收缩。在展开阶段里,构造起一个推迟进行的操作所形成的链条,收缩阶段表现为这些运算符的实际执行。这种类型的计算过程由一个推迟执行的链条刻画,称为一个递归计算过程。要执行这种过程,编译器就需要维护好那些以后将要执行的操作的轨迹。而这个保存的信息量与n成线性关系,所以该过程是线性递归过程
与之相对应,第二个计算过程里并没有任何增长和收缩,对于任何一个n,在计算过程中的每一步,在我们所有需要保存的轨迹里,所以的东西就是变量product,cnt,max_cnt的当前值。我们称这一过程为一个迭代计算过程。所需的计算步骤随着n线性增长,这种过程称为线性迭代过程。一般来所迭代计算过程就是那种其状态可以用固定数目的状态变量描述的计算过程,而与此同时,又存在着一套固定的规则,描述了计算过程从一个状态到下一状态转换时,这些变量的更新方式;还有一个结束检测,它描述着一计算过程应该终止的条件
我们还可以从另一个角度来看这两个过程之间的对比。在迭代的情况里,在计算过程中的任何一点,那几个程序变量都提供了有关计算状态的一个完整描述。如果我们令上述计算在某两步之间停下来,要想重新唤醒这一计算,只需为解释器提供有关这三个变量的值。而对于递归计算过程而言,这里还存在着另外的一些隐含信息,它们并未保存在程序变量里,而是由解释器维持着,指明了在所推迟的运算所形成的链条里的漫游中,"这一计算过程处在何处"。这个链条越长,需要保存的信息也就越多。
在做迭代与递归之间的比较时,我们必须小心,不要搞混了递归计算过程的概念和递归过程的概念。当我们说一个过程是递归的时候,论述的是一个语法形式上的事实,说明这个过程的定义中(直接或间接地)引用了该过程本身。在说某一计算过程具有某种模式时(如线性递归),我们说的是这一计算过程的进展方式,而不是相应过程书写上的语法形式。
现在再来个斐波那契数列的例子。定义如下:
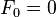
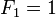
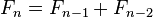
(n>=2)
可以轻松写出前几项0 1 1 2 3 5 8 13 … (特别指出:0不是第一项,而是第零项。)
根据定义很快就可以翻译成如下代码
int fib(int n)
{
if(n == 0)
{
return 0;
}
if(n == 1)
{
return 1;
}
return fib(n-1) + fib(n - 2);
}
很明显上面是递归的过程。上一个状态可以推导出下一个状态,但是下一个状态的值又影响到上一个状态。
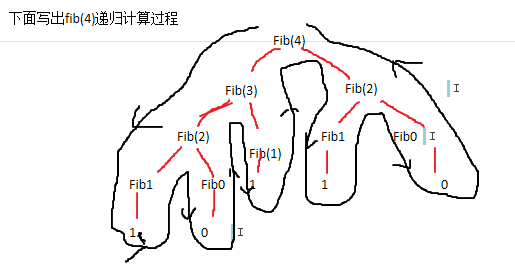
再来考虑怎么用迭代计算,用一对整数a和b,将他们分别初始化为fib(1) = 1, fib(0) = 0, 反复的使用下面的变换规则:
a+b -> a
a -> b
下面是迭代版本的代码:
int fib_iter(int a, int b,int cnt) { if(cnt == 0) { return b; } return fib_iter(a+b, a, cnt - 1); } int fib(int n) { return fib_iter(1, 0, n); }
注:
本文中的例子来之《计算机程序的构造和解释》