算法导论数论计算x^2=1(mod n) 在区间[1,n1]的解

计算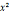=1(modn)在区间[1,n-1]的解

1.n=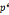,p为奇素数

因为，所以必有原根，设n=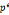

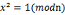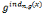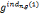        ,=(modn),)==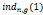0(modφ(n))

φ(n)=(p-1)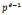,gcd(2,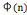)=2,d=2,且0|2，有两个解，1，n-1.

2.n=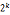

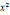-1=0(mod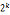) 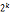，|(x+1)(x-1)，因为x为奇数，所以(x-1)(x+1)为相邻偶数

所以一个能被2整除，一个能被4整除，能被4整除的那个必能被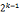整除

(1) k>2解：x=±1(mod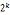)和x=(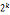±1)(mod)

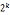(2) k=2解：x=1,3

(3) k=1解：x=1

3. 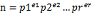（e1,e2,…,er>0）

那么x²=1(mod n)中国剩余x²=1(mod p_i^ei)。

(1)pi!=2解：1，n-1

(2)pi=2

1) k>2解：x=±1(mod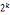)和x=(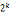±1)(mod)

2) k=2解：x=1,3

3) k=1解：x=1

根据中国剩余定理，所有素因子的每一组可能值都对应了方程的一个解， 由乘法原理，可以得出方程的解的数目为：2^{(r+[8|m]+[4|m]-[2|m])}