用牛顿迭代法求下面方程在1.5附近的根:
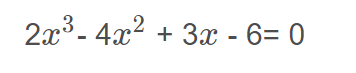
答案解析:
牛顿迭代法的公式为:
(x_{n+1}) = (x_{n}) - (frac{f(x_{n})}{f'(x_{n})})
其中,(x_{n})为输出的值,在该题目当中为1.5。(f(x_{n}))为公式2(x^3)- 4(x^2) + 3(x) - 6。(f'(x_{n}))为导数,根据导数原则:
规则1:(x^n) = n * (x^{(n-1)}), 规则2:常数的导数为0。可以推导出(f'(x_{n})) = 6(x^2) - 8x + 3。
在依照牛顿迭代法计算出(x_{n+1})的值,直到求出的差值小于0.00001
代码示例:
#include <stdio.h>
#include <math.h>
int main()
{
double x1, x0, f, f1;
x1 = 1.5;
do
{
x0 = x1;
f = ((2 * x0 - 4) * x0 + 3) * x0 - 6;
f1 = (6 * x0 - 8) * x0 + 3;
x1 = x0 - f / f1;
} while (fabs(x1 - x0) >= 1e-5);
printf("方程在1.5附近的根为:%lf
", x1);
return 0;
}
运行截图: