素数判定Miller_Rabin 算法详解

最简单直观简单的素数判定方法就是试除法。对于判断数n是否是素数，我们从2开始一直到sqrt(n)。如果找到一个因子则判断n不是素数，否则是素数。代码如下：

bool isPrime( long long n )
{
    for(long long i = 2; i*i <= n; i++)
    {
        if(n%i == 0) return false;
    }
    	return true;
}        

　　

如果要找到成1~n的所有素数那么这个时间代价就变为O(n^2)，很多时候是不可接受的。
所以随着学习的深入，我们了解到了素数筛法，即从2开始，2的倍数肯定不是素数，再向右扫描，如果扫描到素数，则重复之前的过程，剔除之后的部分合数（准确的说是关于当前质数的倍数），如果扫描到合数则跳过（表示前面已经更新过这个数不是素数）。然后都扫描一遍即可把1~n的素数求解出来。这个算法的复杂度略高于O(n)。素数筛代码如下：

bool isprime[MAXN];
int prime[MAXN];
int cnt = 0;//保存素数个数
void getPrime()
{
	for(int i = 1; i < MAXN; i++)
		isprime[i] = true; 
                //先假设所有数是素数，后面逐个扫描更新
	for(int i = 2; i < MAXN; i++) //扫一遍
	{
		if(!isprime[i]) continue; 
                //如果不是素数，则不往后面更新
		
		prime[cnt++] = i;
		for(int j = 2 * i; j < MAXN; j += i)
			isprime[j] = false;
	}
}

但是这个算法的弊端在于，为了判断一个大数是否是素数必须从从头开始扫描，而且空间代价也受不了，故不能离散的判断。

Miller_rabin算法

算法的理论基础：

1. Fermat定理：

若n是奇素数，a是任意正整数(1≤ a≤ n−1)，

证明：由费马定理，可以排除大部分非素数的情况（满足费马定理是素数的必要条件），给出一个奇素数n，显然n-1为一个偶数，存在,显然（q，m为任意整数）是成立的，所以,显然.

2. 二次探测定理：

　　证明过程如下：

　　

　　由p为一个素数可以推出。

　　所以根据二次探测定理，可以推断,……,.

3. 综上：

对于一个大数n，判断n是不是素数的时候，可以先考虑a^（n-1）≡ 1（mod n）

对于n-1，一定可以拆分成2^s+d：

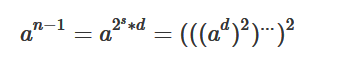
可以从x = a^d开始，依次平方s次，每次平方的时候模上n，按照之前的平方根定理，如果模上n的结果为1的话，那么x一定是1，或者是n-1，如果不满足则不是素数，x=x²，再次循环。

每次随机选一个在2-n-1的数字作为a，可以重复测试。

由于mod上的是n，n是一个大数，所以快速幂中的乘法，需要用快速加法来实现。不然就算模上之后再相乘也会溢出。

代码：

#include <iostream> 
#include <cstdio> 
#include <algorithm>  
#include <cmath>  
#include <cstring>  
#include <map>  
using namespace std;
 
const int times = 20;
int number = 0;
 
map<long long, int>m;
long long Random( long long n )			
//生成[ 0 , n ]的随机数
{
	return ((double)rand( ) / RAND_MAX*n + 0.5);
}
 
long long q_mul( long long a, long long b, long long mod ) 
{//快速计算 (a*b) % mod
	long long ans = 0;
	while(b)
	{
		if(b & 1)
		{
			b--;
			ans =(ans+ a)%mod;
		}
		b /= 2;
		a = (a + a) % mod;
 
	}
	return ans;
}
 
long long q_pow( long long a, long long b, long long mod ) 
{//快速计算 (a^b) % mod
	long long ans = 1;
	while(b)
	{
		if(b & 1)
		{
			ans = q_mul( ans, a, mod );
		}
		b /= 2;
		a = q_mul( a, a, mod );
	}
	return ans;
}
 
bool witness( long long a, long long n )//miller_rabin算法的精华
{//用检验算子a来检验n是不是素数
	long long tem = n - 1;
	int j = 0;
	while(tem % 2 == 0)
	{
		tem /= 2;
		j++;
	}
	//将n-1拆分为a^r * s
 
	long long x = q_pow( a, tem, n ); 
	//得到a^r mod n
	if(x == 1 || x == n - 1) return true;	
	//余数为1则为素数
	while(j--) //否则试验条件2看是否有满足的 j
	{
		x = q_mul( x, x, n );
		if(x == n - 1) return true;
	}
	return false;
}
 
bool miller_rabin( long long n )  
{//检验n是否是素数
 
	if(n == 2)
		return true;
	if(n < 2 || n % 2 == 0)
		return false;				
		//如果是2则是素数，如果<2或者是>2的偶数则不是素数
 
	for(int i = 1; i <= times; i++)  //做times次随机检验
	{
		long long a = Random( n - 2 ) + 1; 
		//得到随机检验算子 a
		if(!witness( a, n ))						
		//用a检验n是否是素数
			return false;
	}
	return true;
}
 
 
int main( )
{
	long long tar;
	while(cin >> tar)
	{
		if(miller_rabin( tar ))	//检验tar是不是素数
			cout << "Yes, Prime!" << endl;
		else
			cout << "No, not prime.." << endl;
	}
	return 0;
}

　　

部分参考：https://www.cnblogs.com/fzl194/p/9046117.html