http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=2906
11806 - Cheerleaders
Time limit: 2.000 seconds
In most professional sporting events, cheerleaders play a major role in entertaining the spectators. Their roles are substantial during breaks and prior to start of play. The world cup soccer is no exception. Usually the cheerleaders form a group and perform at the centre of the field. In addition to this group, some of them are placed outside the side line so they are closer to the spectators. The organizers would like to ensure that at least one cheerleader is located on each of the four sides. For this problem, we will model the playing ground as an M × N rectangular grid. The constraints for placing cheerleaders are described below:
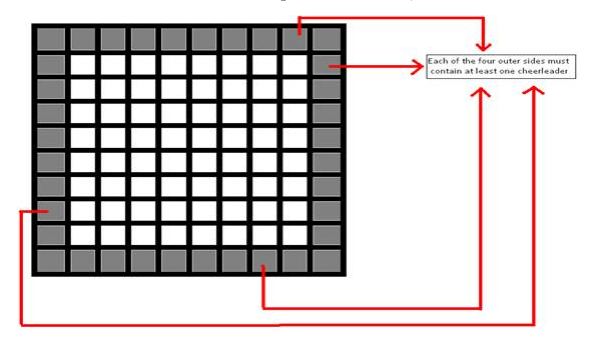
• There should be at least one cheerleader on each of the four sides. Note that, placing a cheerleader on a corner cell would cover two sides simultaneously.
• There can be at most one cheerleader in a cell.
• All the cheerleaders available must be assigned to a cell. That is, none of them can be left out.
The organizers would like to know, how many ways they can place the cheerleaders while maintaining the above constraints. Two placements are different, if there is at least one cell which contains a cheerleader in one of the placement but not in the other.
Input
The first line of input contains a positive integer T ≤ 50, which denotes the number of test cases. T lines then follow each describing one test case. Each case consists of three nonnegative integers, 2 ≤ M, N ≤ 20 and K ≤ 500. Here M is the number of rows and N is the number of columns in the grid. K denotes the number of cheerleaders that must be assigned to the cells in the grid.
Output
For each case of input, there will be one line of output. It will first contain the case number followed by the number of ways to place the cheerleaders as described earlier. Look at the sample output for exact formatting. Note that, the numbers can be arbitrarily large. Therefore you must output the answers modulo 1000007.
Sample Input
2
2 2 1
2 3 2
Sample Output
Case 1: 0
Case 2: 2
分析:
暴力枚举、
AC代码:
1 // UVa11806 Cheerleaders 2 3 #include<cstdio> 4 5 #include<cstring> 6 7 using namespace std; 8 9 10 11 const int MOD = 1000007; 12 13 const int MAXK = 500; 14 15 int C[MAXK+10][MAXK+10]; 16 17 18 19 int main() { 20 21 memset(C, 0, sizeof(C)); 22 23 C[0][0] = 1; 24 25 for(int i = 0; i <= MAXK; i++) { 26 27 C[i][0] = C[i][i] = 1; // 千万不要忘记写边界条件 28 29 for(int j = 1; j < i; j++) 30 31 C[i][j] = (C[i-1][j] + C[i-1][j-1]) % MOD; 32 33 } 34 35 36 37 int T; 38 39 scanf("%d", &T); 40 41 for(int kase = 1; kase <= T; kase++) { 42 43 int n, m, k, sum = 0; 44 45 scanf("%d%d%d", &n, &m, &k); 46 47 for(int S = 0; S < 16; S++) { // 枚举所有16种“搭配方式” 48 49 int b = 0, r = n, c = m; // b用来统计集合的个数,r和c是可以放置的行列数 50 51 if(S&1) { r--; b++; } // 第一行没有石头,可以放石头的行数r减1 52 53 if(S&2) { r--; b++; } 54 55 if(S&4) { c--; b++; } 56 57 if(S&8) { c--; b++; } 58 59 if(b&1) sum = (sum + MOD - C[r*c][k]) % MOD; // 奇数个条件,做减法 60 61 else sum = (sum + C[r*c][k]) % MOD; // 偶数个条件,做加法 62 63 } 64 65 printf("Case %d: %d ", kase, sum); 66 67 } 68 69 return 0; 70 71 }