https://www.luogu.com.cn/problem/P1025
题目描述
将整数n分成k份,且每份不能为空,任意两个方案不相同(不考虑顺序)。
例如:n=7,k=3,下面三种分法被认为是相同的。
1,1,5;
1,5,1;
5,1,1.
问有多少种不同的分法。
输入格式
n,k (6<n≤200,2≤k≤6)
输出格式
1个整数,即不同的分法。
输入输出样例
7 3
4
说明/提示
四种分法为:
1,1,5;
1,2,4;
1,3,3;
2,2,3.
解法一(DFS):
DFS算是比较容易想到的,但需要剪枝。
void DFS(int sum,int step,int k)
k 表示上一份分了多少个,这次就从k个开始分,sum表示到目前为止一共分了多少个,step表示到目前为止一共分了多少份。
由于方案数不能相同,所以枚举的个数要保持递增(或递减),我们可以进行重复性剪枝,记录k(上一份分了多少个),这次就从k个开始分起。
同时我们还要进行可行性剪枝,每次只要i从k枚举到i*(m - step) <= n-sum 就可以了。
因为下一份分的值不能比当前的i小,假设以后每份都分i,那么如果i*(m - step) > n-sum,则说明剩余的值不够分了,当前的i就不可行了,不需要继续DFS了。
1 #include <stdio.h> 2 #include <string.h> 3 #include <iostream> 4 #include <string> 5 #include <math.h> 6 #include <algorithm> 7 #include <vector> 8 #include <stack> 9 #include <queue> 10 #include <set> 11 #include <map> 12 #include <sstream> 13 const int INF=0x3f3f3f3f; 14 typedef long long LL; 15 const int mod=1e9+7; 16 const int maxn=1e4+10; 17 using namespace std; 18 19 int n,m; 20 int ans; 21 22 void DFS(int sum,int step,int k)//k表示上一份分到了多少个,重复性剪枝 23 { 24 if(step==m) 25 { 26 if(sum==n) ans++; 27 return ; 28 } 29 for(int i=k;i*(m-step)<=n-sum;i++)//可行性剪枝 30 DFS(sum+i,step+1,i); 31 } 32 33 int main() 34 { 35 #ifdef DEBUG 36 freopen("sample.txt","r",stdin); 37 #endif 38 39 scanf("%d %d",&n,&m); 40 DFS(0,0,1); 41 printf("%d ",ans); 42 43 return 0; 44 }
解法二(DP):
dp[ i ][ j ]表示将整数 i 划分为 j 份 的方案数。
首先,如果拿到一个整数 i ,因为题目中要求每份不能为空,因此必须先拿出 j 个数位将 j 份分别放上1,此时剩下 i - j个数。
那么剩下的数如何处理呢?可以将其全部分到一份当中(dp[ i-j ][1]),也可以分到两份中(dp[ i-j ][2]),...,也可以分到 j 份中(dp[ i-j ][ j ]),将每一种分法全部加起来,和即为dp[ i ][ j ]。
![]()
不过这个式子看起来并不简洁,为了求得一个简洁的式子,我们再求一个dp[i-1][j-1],
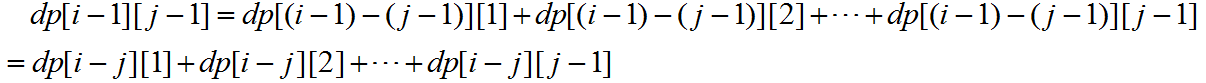
比较上面两个式子可得,
![]()
上式对应两种情况:
1.有一份只分了一个1,剩下的 i-1 要分成 j-1 份,对应dp[ i-1 ][ j-1 ]。
2.每一份的值都大于1,也就是先在j份中,每一份都放一个1,然后还剩下 i-j 个,再把这 i-j 个再分给这 j 份,对应dp[ i-j ][ j ]。(此时 i 必须大于 j )
1 #include <stdio.h> 2 #include <string.h> 3 #include <iostream> 4 #include <string> 5 #include <math.h> 6 #include <algorithm> 7 #include <vector> 8 #include <stack> 9 #include <queue> 10 #include <set> 11 #include <map> 12 #include <sstream> 13 const int INF=0x3f3f3f3f; 14 typedef long long LL; 15 const int mod=1e9+7; 16 const int maxn=1e4+10; 17 using namespace std; 18 19 int dp[205][10]; 20 21 int main() 22 { 23 #ifdef DEBUG 24 freopen("sample.txt","r",stdin); 25 #endif 26 27 int n,m; 28 scanf("%d %d",&n,&m); 29 for(int i=1;i<=n;i++) 30 { 31 dp[i][1]=1; 32 for(int j=2;j<=m;j++) 33 { 34 if(i==j) dp[i][j]=1; 35 else if(i>j) dp[i][j]=dp[i-1][j-1]+dp[i-j][j]; 36 } 37 } 38 printf("%d ",dp[n][m]); 39 40 return 0; 41 }
-