区区区间间间（单调栈）

链接：https://ac.nowcoder.com/acm/problem/20806
来源：牛客网

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 32768K，其他语言65536K
64bit IO Format: %lld

题目描述

输入描述:

第一行输入数据组数T
对于每组数据，第一行为一个整数n，表示序列长度
接下来一行有n个数，表示序列内的元素

输出描述:

对于每组数据，输出一个整数表示答案

示例1

输入

3
3
4 2 3
5
1 8 4 3 9
20
2 8 15 1 10 5 19 19 3 5 6 6 2 8 2 12 16 3 8 17 

输出

5
57
2712

说明

对于一组测试数据的解释：
区间[1, 2]的贡献为：4 - 2 = 2
区间[1, 3]的贡献为：4 - 2 = 2
区间[2, 3]的贡献为：3 - 2 = 1
2 + 1 + 2 = 5.

备注:

T⩽20,n⩽10⁵,0⩽a_i​⩽10⁵

不保证数据随机生成！

该题就是求所有子区间（子区间长度大于1，至少为2）的最大值减去最小值的和是多少。

可以对原式拆分一下得：

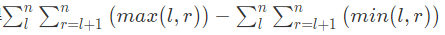
其中max(l, r)表示区间l到r的最大值，min(l, r)表示区间l到r的最小值。

那么问题就转化为：求所有区间长度大于1的子区间的最大值之和与最小值之和。

我们以求最大值为例：

我们考虑用单调栈去a_i左边和右边第一个比它大的位置，进而求出区间个数。

用L[i]表示以a[i]为最大值，向左最多延伸到L[i]，R[i]表示以a[i]为最大值，向右最多延伸到R[i]。

正着跑一次单调栈，倒着跑一次单调栈就能求出来L和R数组。

那么对于每一个a[i]，设满足a[i]为区间最值的区间个数num，那么a[i]对ans的贡献就是a[i] * num，那么我们知道了L[i]和R[i]，怎样求num呢？

有两种理解方式：

方式一：分两种情况。num = num1+num2

情况一：a[i]作为一个区间的端点，那么可以选择的区间另一个端点，可选择端点个数也就等于区间个数，num1 = R[i]-L[i]（当R[i]=L[i]时，也就是区间长度为1时，R[i]-L[i]=0，对答案没影响）。

情况二：a[i]作为区间中的一点，那么要选择区间的左右两个端点。在L[i]到i之间选一个作为左端点，R[i]-i之间选一个作为右端点，乘法原理可得区间的个数num2 = (R[i]-i) * (i-L[i])

num = num1+num2 = R[i]-L[i] + (R[i]-i) * (i-L[i])

方式二：直接num = (R[i]-i+1) * (i-L[i]+1) - 1

举个例子：1 2 3 4 5，求必须包含3的区间个数，左边有3种选择：[1 2]；[2]；不选；，右边也有三种选择：[4 5]；[4]；不选；但是题目中要求区间长度至少为2，所以两边都不选的情况要减去。

有个小技巧：求最小值时，我们可以让a[i] = -a[i]，那么求最小值，就等于取反后的求最大值，再按照上面的过程求一下就好了（注意因为取了相反数，故最后求出来的和也带负号，故最后不是-而是+）。

有一个坑点就是如果数组中相邻元素重复的情况会导致最终区间重复计算，为了防止重复，求左右拓展范围的时候第一遍扫带等号，第二遍扫不带等号（或者第一遍不带等号，第二遍带）

即单调栈中一个arr[i]>=arr[sk.top()]，另一个是arr[i]>arr[sk.top()]。

举个例子：5 6 5。这种情况很明显只有三个区间[5 6]，[5 6 5]，[6 5]，即最终要减去15。

但是如果都用>=，那么每个位置对应的区间(Li, Ri)分别为(1, 3)，(2, 2)，(1, 3)。最终却减去了20，可以发现[1,3]区间被减了两次。

再举个例子：2 1 2。这种情况的最大值2对应的很明显只有3个区间[2 1]，[2 1 2]，[1 2]，即最终要加上2*3=6。

但是如果都用>=，那么每个位置对应的区间(Li, Ri)分别为(1, 3)，(2, 2)，(1, 3)。最终却加上了8。可以发现[1,3]区间被加了两次，所以需要保证相等的时候一端扩展，避免重复计算。

两种写法：

写法一：

#include <bits/stdc++.h>
typedef long long LL;
#define pb push_back
#define mst(a) memset(a,0,sizeof(a))
const int INF = 0x3f3f3f3f;
const double eps = 1e-8;
const int mod = 1e9+7;
const int maxn = 1e5+10;
using namespace std;

int a[maxn], b[maxn];
int L[maxn], R[maxn];
stack<int> sk;

LL solve(int arr[], int n)
{
    while(!sk.empty()) sk.pop();
    for(int i=1;i<=n;i++)
    {
        while(!sk.empty()&&arr[i]>=arr[sk.top()])
            sk.pop();
        L[i] = sk.empty()? 1:sk.top()+1;
        sk.push(i);
    }
    while(!sk.empty()) sk.pop();  //别忘了
    for(int i=n;i>=1;i--)
    {
        while(!sk.empty()&&arr[i]>arr[sk.top()])  //这里用>而不是>=
            sk.pop();
        R[i] = sk.empty()? n:sk.top()-1;
        sk.push(i);
    }
    LL res = 0;
    for(int i=1;i<=n;i++)
        res += arr[i] * ((LL)(i-L[i]+1)*(R[i]-i+1)-1); //记得加LL
    return res;
}


int main()
{
    #ifdef DEBUG
    freopen("sample.txt","r",stdin); //freopen("data.out", "w", stdout);
    #endif
    
    int T;
    scanf("%d",&T);
    while(T--)
    {
        int n;
        scanf("%d",&n);
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&a[i]);
            b[i] = -a[i];
        }
        LL maxsum = solve(a, n);
        LL minsum = solve(b, n); //已经取负过了
        printf("%lld
",maxsum+minsum);
    }
    
    return 0;
}

写法二：

#include <bits/stdc++.h>
typedef long long LL;
#define pb push_back
#define mst(a) memset(a,0,sizeof(a))
const int INF = 0x3f3f3f3f;
const double eps = 1e-8;
const int mod = 1e9+7;
const int maxn = 1e5+10;
using namespace std;

int a[maxn], b[maxn];
int L[maxn], R[maxn];

LL solve(int arr[], int n)
{
    for(int i=1;i<=n;i++)
    {
        int pos = i;
        while(pos>1&&arr[i]>=arr[pos-1])
            pos = L[pos-1];
        L[i] = pos;
    }
    for(int i=n;i>=1;i--)
    {
        int pos = i;
        while(pos<n&&arr[i]>arr[pos+1])
            pos = R[pos+1];
        R[i] = pos;
    }
    LL res = 0;
    for(int i=1;i<=n;i++)
    {
        res += (LL)arr[i] * (R[i]-L[i]);
        res += (LL)arr[i] * (i-L[i])*(R[i]-i);
    }
    return res;
}

int main()
{
    #ifdef DEBUG
    freopen("sample.txt","r",stdin); //freopen("data.out", "w", stdout);
    #endif
    
    int T;
    scanf("%d",&T);
    while(T--)
    {
        int n;
        scanf("%d",&n);
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&a[i]);
            b[i] = -a[i];
        }
        LL maxsum = solve(a, n);
        LL minsum = solve(b, n); //已经取负过了
        printf("%lld
",maxsum+minsum);
    }
    
    return 0;
}

看到有别的写法，粘一下，可以研究研究：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;//要用long long
int read(){
    int sum = 0;
    char ch = getchar();
    while(!isdigit(ch)) ch = getchar();
    while(isdigit(ch)) { sum = (sum<<1)+(sum<<3)+(ch^48);ch = getchar();}
    return sum;
}//数据量大，用快读
const int N=100005;
int t,n,a[N],s[N];//s为单调递减栈,保存的是下标，单调递减指的是下标对应a数组元素的单调递减
 
//返回最大（小）值的和
ll solve(){
    int top = 0;//栈顶
    ll ans = 0,sum = 0;//要用long long
    //ans是最后要返回的各个区间最大（小）值的和，sum是所有以当前位置为右端点的前面各个区间最大（小）值的和
    for(int i = 1;i <= n;i++){
        //如果栈不空并且单调递减栈的单调性将在i进入后被破坏，就要退栈清算sum
        while(top != 0 && a[ s[top] ] < a[i]){
            sum -= (ll)(s[top] - s[top-1]) * a[ s[top] ];//因为区间最大值被改变，所以sum要减掉之前比i小的部分贡献（不理解的话就动手模拟一下，再看一下sum的定义）
            //要转long long，不然只有70分
            top--;
        }
        s[++top] = i;//不管怎么样，i都要入栈的
        sum += (ll)(s[top] - s[top-1]) * a[ s[top] ];//s[top]其实就是i，这里这样写是为了保持和上面while循环式子的一致性（好看）
        //要转long long，不然只有70分
        ans += sum;
    }
    return ans;
}
 
int main(){
    t = read();
    while(t--){
        n = read();
        for(int i = 1;i <= n;i++) a[i] = read();
        ll zheng = solve();//求在所有区间最大值的和
        for(int i = 1;i <= n;i++) a[i] = -a[i];//a[i]原来都是非负实数，取负号后最大值就是原最小值
        ll fu= solve();//求在所有区间最小值的和并取了负
        cout<<fu+zheng<<endl;//最大值的和-最小值的和
    }
    return 0;
}

-