矩阵标准差在神经网络中的反向传播以及数值微分梯度验证

最近开脑洞想训练一个关于球面拟合的模型于是用到了标准差作为输出层的损失函数，所以就对于标准差方程进行反向传播推导了一下。

现在分享一下推导过程和结果和用数值微分方法对于结果正确性的验证，顺便记录一下以免忘记了。

这是标准差方程

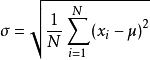
标准差主要是用来描述数据离散程度，其实就是方差的开平方

首先若a为矩阵，那么标准差计算可用numpy实现如下

np.sqrt(np.sum((a - np.mean(a)) ** 2) / a.size);

矩阵标准差数值微分求梯度如下，（这个函数主要用来验证反向传播推导结果）

# 数值微分求标准差梯度
def gradient ():
    d = 1e-5;
    grad = np.zeros(a.size);
    func = lambda : np.sqrt(np.sum((a - np.mean(a)) ** 2) / a.size);
    # func = lambda : np.std(a, ddof = 1);
    # func = lambda : np.mean(a);
    for index, value in enumerate(a):
        bak = value;
        a[index] -= d;
        leftv = func();
        a[index] = bak;
        a[index] += d;
        rightv = func();
        a[index] = bak;
        grad[index] = (rightv - leftv) / (d * 2);
    return grad;

接下来是标准差方程的反向传播推导过程，直接上草稿纸

 

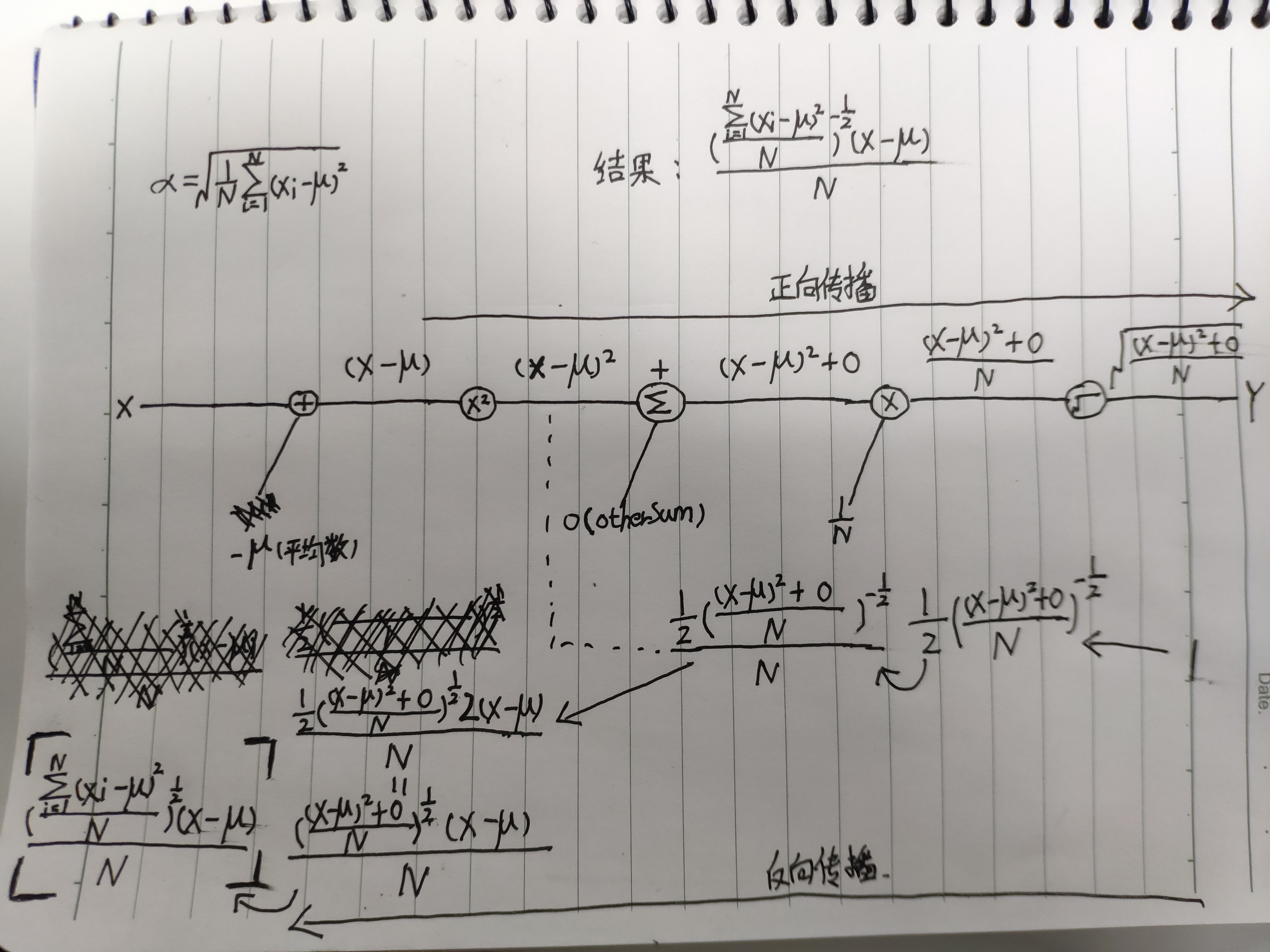
这里初步推导出结果

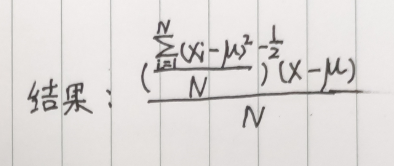
所以，反向传播求标准差方程的Python实现代码如下

这里传入索引可计算矩阵中每一个元素相对于标准差方程的导数，这里没用numpy数组作为参数，可自己修改代码支持矩阵，我就不附上了

def func2 (index):
    # x
    x = a[index];
    # 平均数
    avg = np.mean(a);
    # 平方和
    sqsum = np.sum((a - avg) ** 2);
    # N
    n = a.size;
    print((np.power(sqsum / n, -0.5) * (x - avg)) / n);

 看一下结果

上面是数值微分的结果，下面是反向传播的结果，基本一致，可以证明反向传播推导正确

附上全部代码

#!/usr/bin/env python3
# -*- coding: utf-8 -*-

import numpy as np;

a = np.array([3.0, 3.0, 2.0, 4.9, 100.2, -8.9]);

# 数值微分求标准差梯度
def gradient ():
    d = 1e-5;
    grad = np.zeros(a.size);
    func = lambda : np.sqrt(np.sum((a - np.mean(a)) ** 2) / a.size);
    # func = lambda : np.std(a, ddof = 1);
    # func = lambda : np.mean(a);
    for index, value in enumerate(a):
        bak = value;
        a[index] -= d;
        leftv = func();
        a[index] = bak;
        a[index] += d;
        rightv = func();
        a[index] = bak;
        grad[index] = (rightv - leftv) / (d * 2);
    return grad;

grad = gradient();

def func2 (index):
    # x
    x = a[index];
    # 平均数
    avg = np.mean(a);
    # 平方和
    sqsum = np.sum((a - avg) ** 2);
    # N
    n = a.size;
    return (np.power(sqsum / n, -0.5) * (x - avg)) / n;

print(grad);
n1 = func2(0);
n2 = func2(1);
n3 = func2(2);
n4 = func2(3);
n5 = func2(4);
n6 = func2(5);
b = [n1, n2, n3, n4, n5, n6];
print(b);