形态学,即数学形态学(mathematical Morphology),是图像处理中应用最为广泛的技术之一,主要用于从图像中提取对表达和描绘区域形状有意义的图像分量,使后续的识别工作能够抓住目标对象最为本质〈最具区分能力-most discriminative)的形状特征,如边界和连通区域等。同时像细化、像素化和修剪毛刺等技术也常应用于图像的预处理和后处理中,成为图像增强技术的有力补充。
本文主要包括以下内容
- 二值图像的基本形态学运算, 包括腐蚀、膨胀、开和闭。
- 二值形态学的经典应用, 包括击中击不中变换、边界提取和跟踪、区域填充、提取连通分量、细化和像素化, 以及凸壳
- 灰度图像的形态学运算, 包括灰度腐蚀、灰度膨胀、灰度开和灰度闭
- 本章的典型案例分析
- 在人脸局部图像中定位嘴的中心
- 显微镜下图像的细菌计数
- 利用顶帽变换(top-hat)技术解决光照不均问题
预备知识
在数字图像处理中, 形态学是借助集合论的语言来描述的, 本章后面的各节内容均以本集合论为基础。
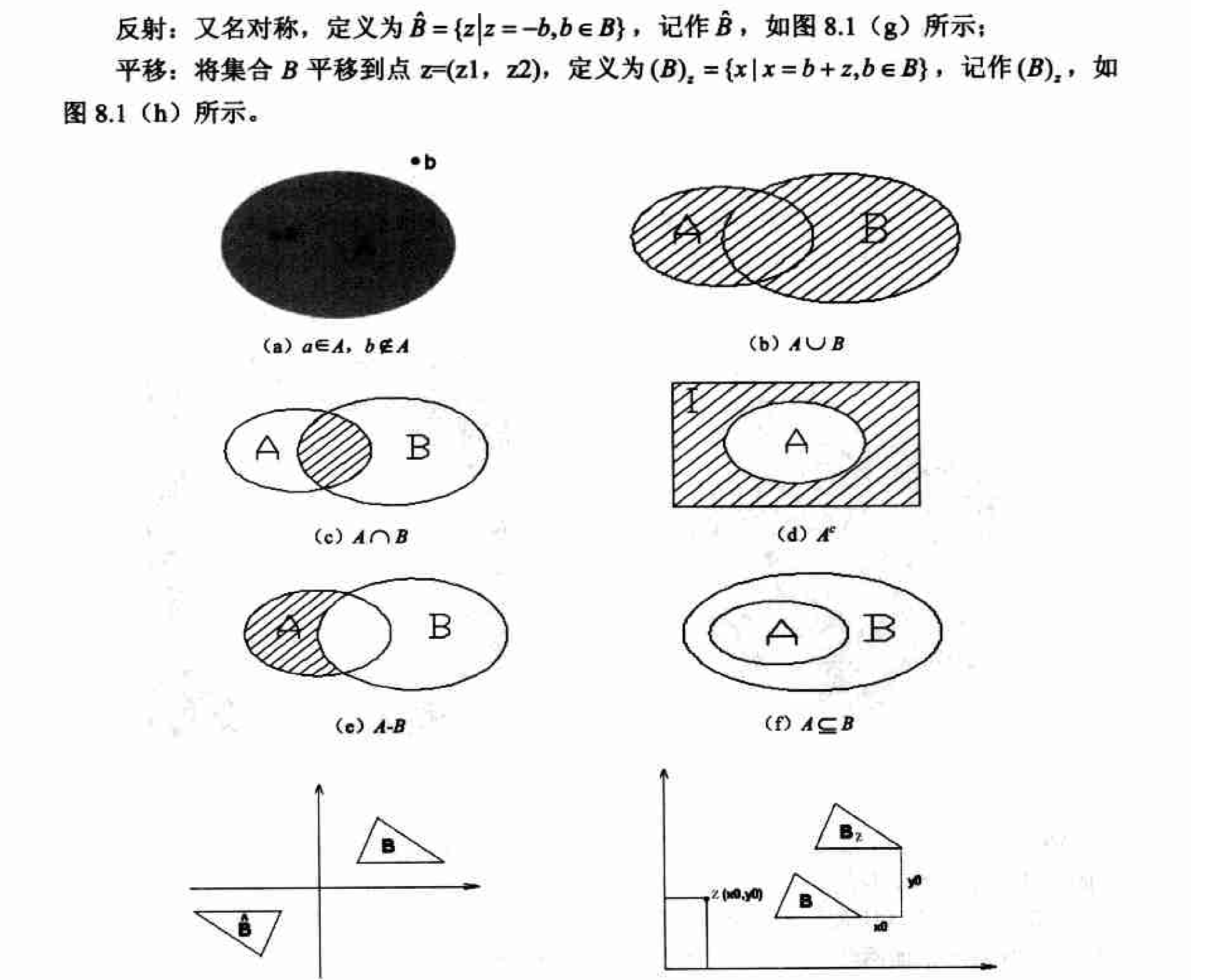
结构元素(structure element)
设有两幅图像A, S。若A是被处理的对象, 而S是用来处理A的, 则称S为结构元素。结构元素通常都是一些比较小的图像, A与S的关系类似于滤波中图像和模板的关系.
二值图像中的基本形态学运算
本节介绍几种二值图像的基本形态学运算, 包括腐蚀、膨胀, 以及开、闭运算。由于所有形态学运算都是针对图像中的前景物体进行的, 因而首先对图像前景和背景的认定给出必要的说明.
注意: 大多数图像,一般相对于背景而言物体的颜色(灰度)更深, 二值化之后物体会成为黑色, 而背景则成为白色, 因此我们通常是习惯于将物体用黑色(灰度值0)表示, 而背景用白色(灰度值255)表示,本章所有的算法示意图以及所有的Visual C++的程序实例都遵从这种约定;但Matlab 在二位图像形态学处理中,默认情况下白色的(二位图像中灰度值为1的像素,或灰度图像中灰度值为255的像素)
是前景(物体),黑色的为背景, 因而本章涉及Matlab 的所有程序实例又都遵从Matlab本身的这种前景认定习惯.
实际上, 无论以什么灰度值为前景和背景都只是一种处理上的习惯, 与形态学算法本身无关。例如对于上面两幅图片, 只需要在形态学处理之前先对图像反色就可以在两种认定习惯之间自由切换。
腐蚀及其实现
腐蚀和膨胀是两种最基本也是最重要的形态学运算, 它们是后续要介绍的很多高级形态学处理的基础, 很多其他的形态学算法都是由这两种基本运算复合而成
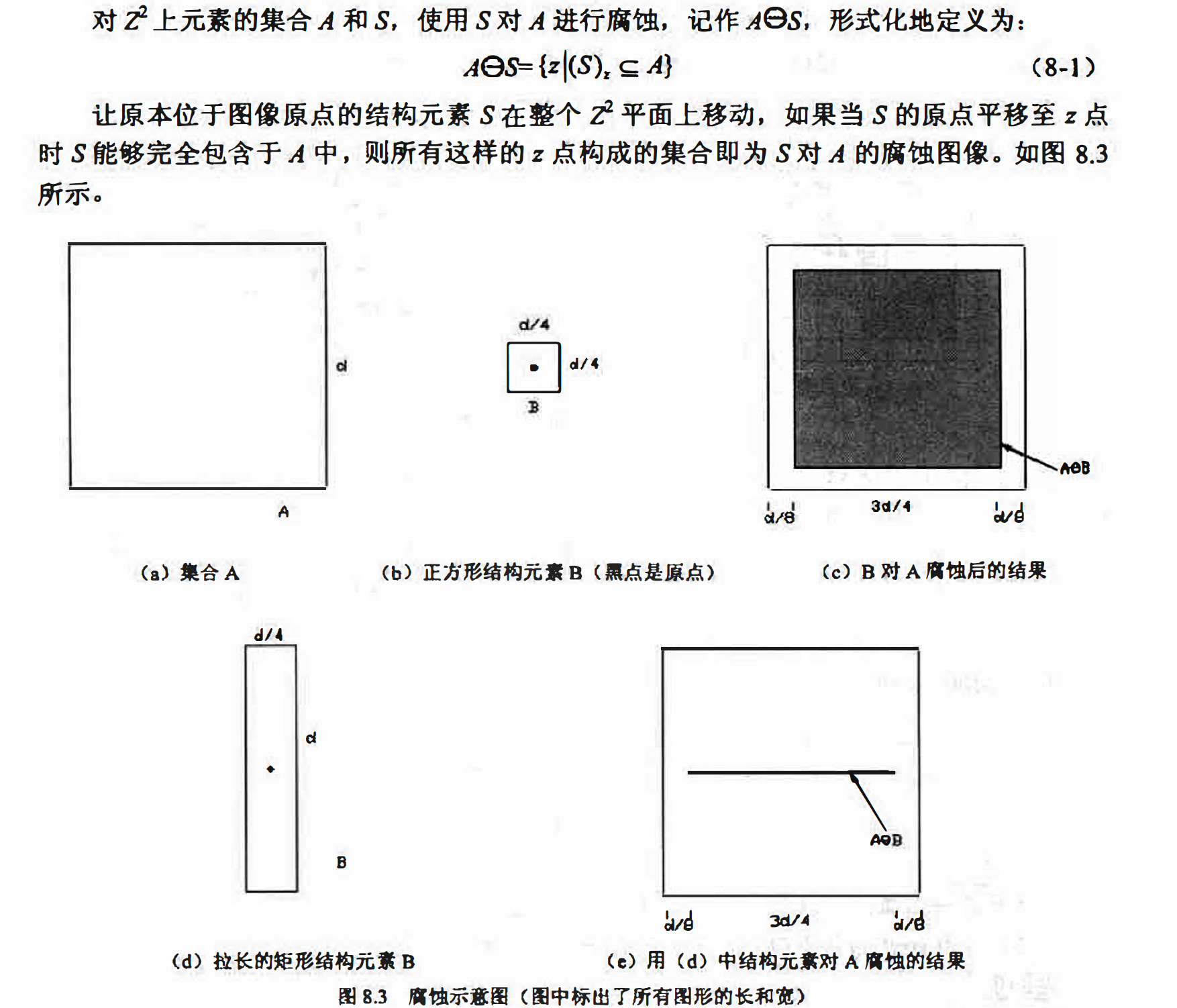
matlab实现
Matlab中与腐蚀相关的两个常用函数为imerode和strel。
imerode函数用于完成图像腐蚀.其常用调用形式如下:I2 = imrode(I,SE)
I为原始图像,可以是二位或灰度图像(对应于灰度腐蚀).
SE是由strel函数返回的自定义或预设的结构元素对象.
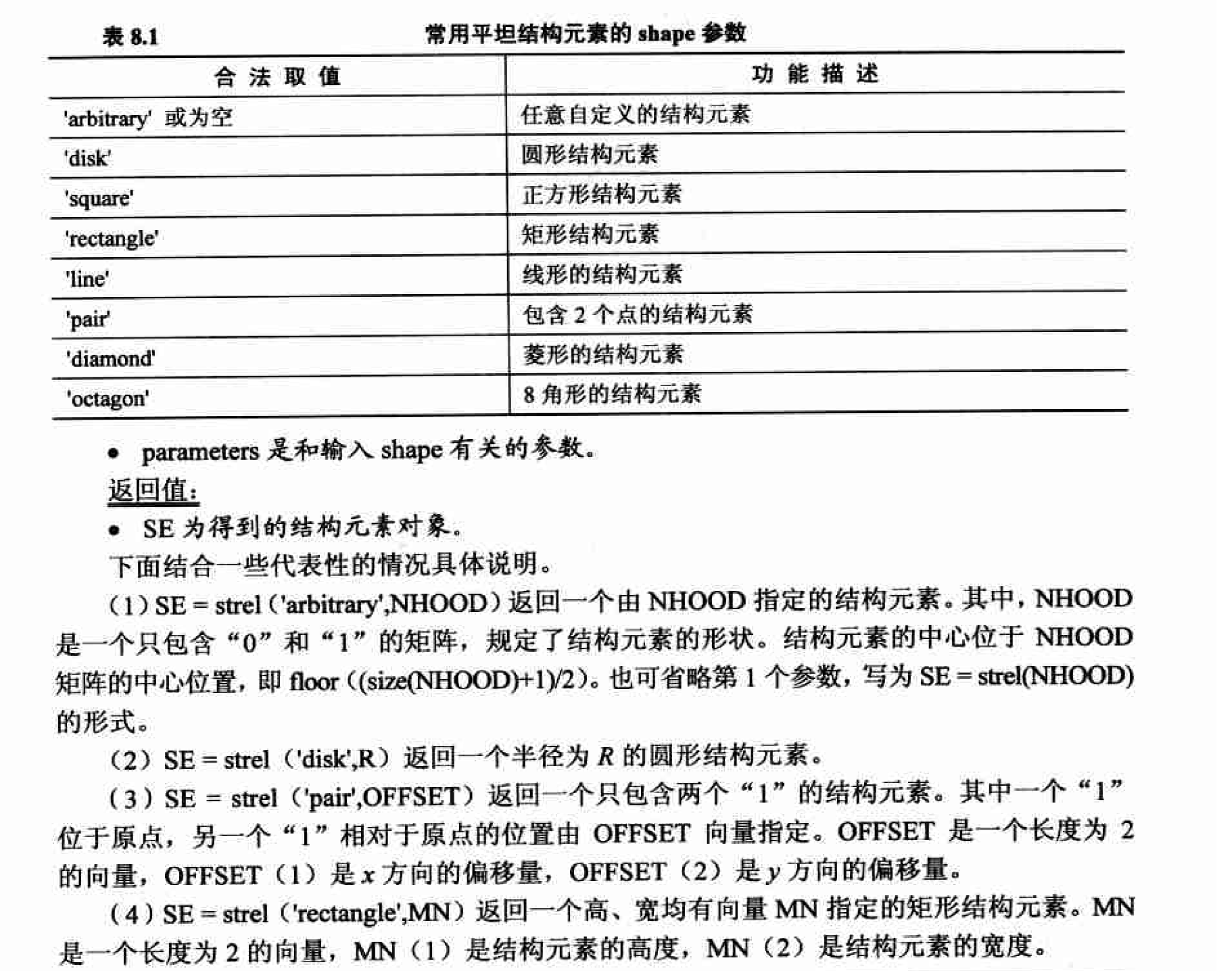
strel函数可以为各种常见形态学运算生成结构元素SE, 当生成供二值形态学使用的结构元素肘, 其调用形式为:SE=strl(shape,parameter)
shape指定了结构元素的形状, 其常用合法取值如在8.1所示.
腐蚀的作用“ 顾名思义,腐蚀能够消融物体的边界,而具体的腐蚀结果与图像本身和结构元素的形状有关。如果物体整体上大于结构元素,腐蚀的结构是使物体变“ 瘦”一圈,而
这一圈到底有多大是由结构元素决定的:如果物体本身小于结构元素, 则在腐蚀后的图像中物体将完全消失:如物体仅有部分区域小于结构元素〈如细小的连通3,则腐蚀后物体会在细
连通处断裂,分离为两部分。
I = imread('erode_dilate.bmp');
se = strel('square',3);
Ib = imerode(I,se);
se = strel([0 1 0;1 1 1;0 1 0]);
Ic = imerode(I,se);
se = strel('square',5);
Id = imerode(I,se);
figure;
subplot(2,2,1);
imshow(I);
subplot(2,2,2);
imshow(Ib);
subplot(2,2,3);
imshow(Ic);
subplot(2,2,4);
imshow(Id);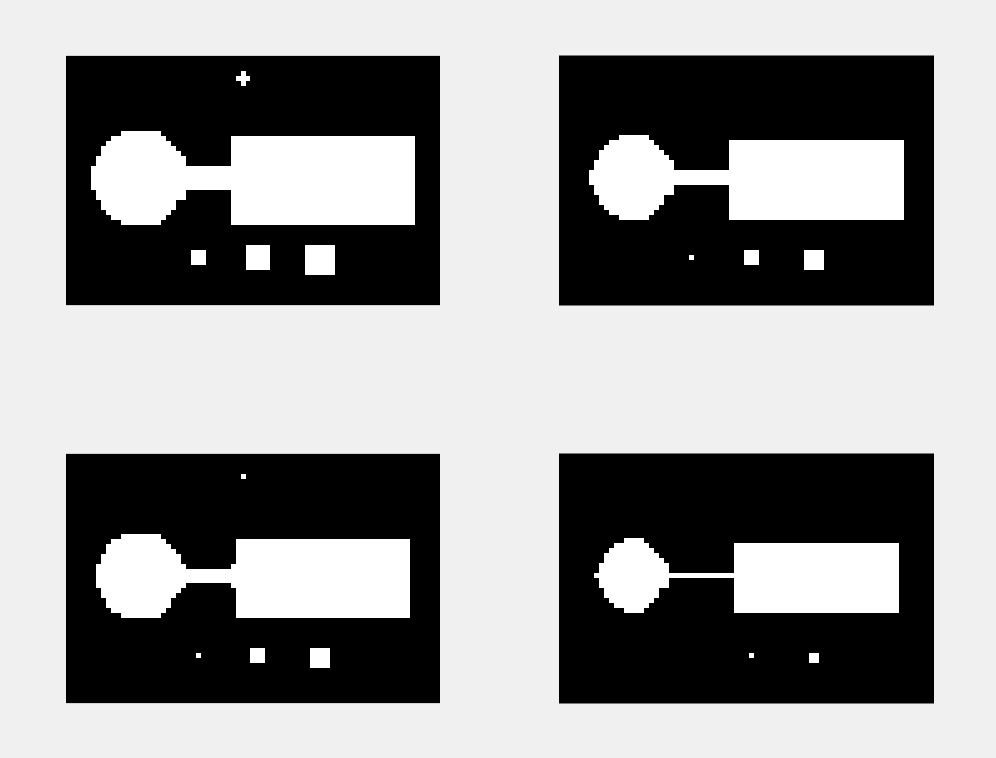
随着腐蚀结构元素的逐步增大,小于结构元素的物体相继消失。由于腐蚀运算具有上述的特点,可以用于滤波。选择适当大小和形状的结构元素,可以滤除掉所有不能 完全包含结构元素的噪声点。然而,利用腐蚀滤除噪声有一个缺点,即在去除噪声点的同时,对图像中前景物体的形状也会有影响,但当我们只关心物体的位置或者个数时,则影响不大
膨胀及其实现
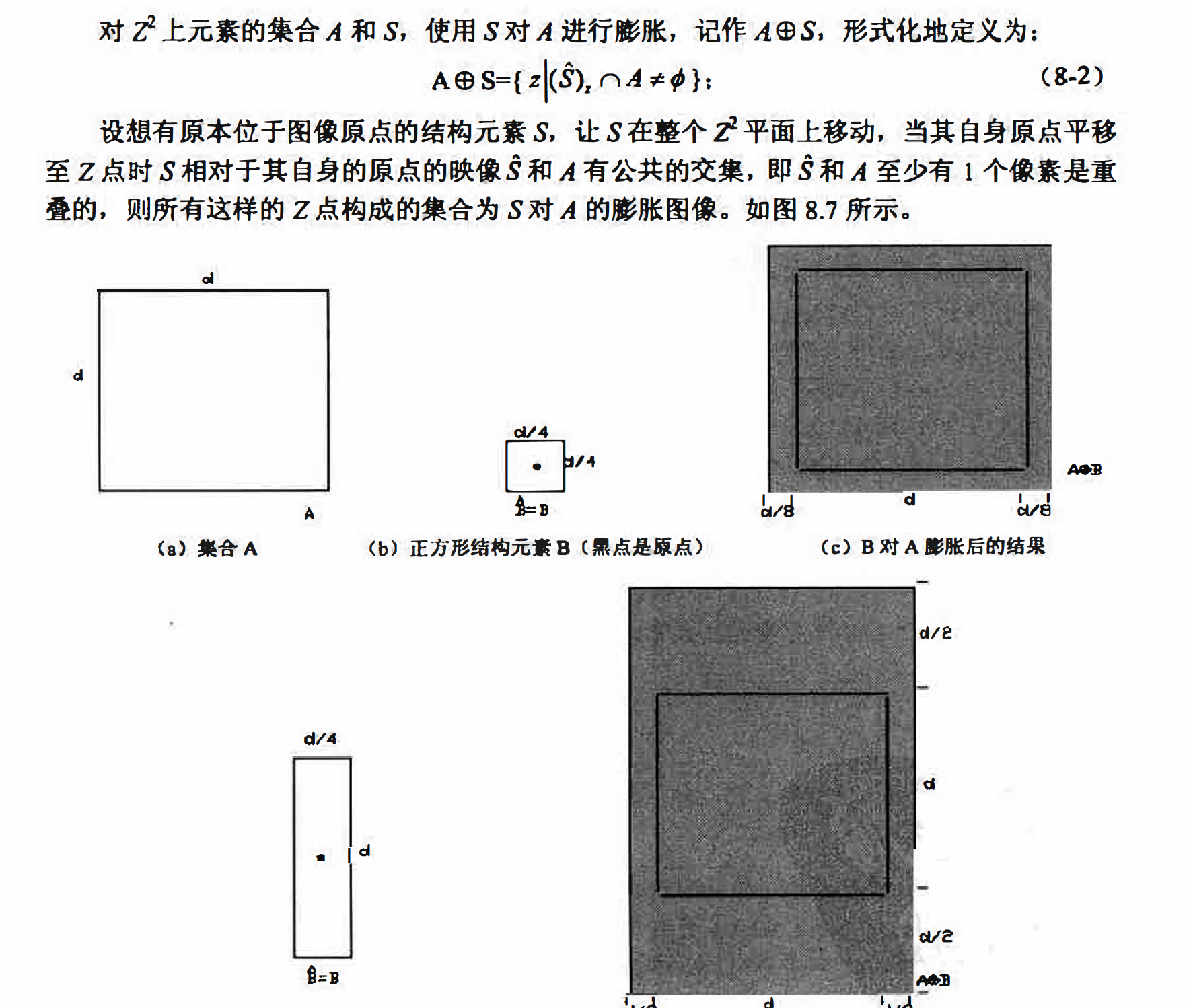
实际上, 膨胀和腐蚀对子集合求补和反射运算是彼此对偶的.
这里值得注意的是定义中要求和A有公共交集的不是结构元素S本身, 而是S的反射集, 觉得熟悉吗?这在形式上似乎容易让我们回忆起卷积运算, 而腐蚀在形式上则更像相关运算。由于图8.8 中使用的是对称的结构元素, 故使用S 和S^' 的膨胀结果相同:但对于图8.9中非对称结构元素的膨胀示例, 则会产生完全不同的结果, 因此在实现膨胀运算时一定要先计算S^'
matlab实现
imdilate函数用于完成图像膨胀, 其常用调用形式如下:
I2 = imdilate(I,SE);
I为原始图像, 可以是二位或灰度图像(对应于灰度膨胀).
SE是由strel函数返回的自定义或预设的结构元素对象
膨胀的作用和腐蚀相反, 膨胀能使物体边界扩大, 具体的膨胀结果与图像本身和结构元素的形状有关。膨胀常用于将图像中原本断裂开来的同一物体桥接起来, 对图像进行二值化之后, 很容易使一个连通的物体断裂为两个部分, 而这会给后续的图像分析(如要基于连通区域的分析统计物体的个数〉造成困扰,此时就可借助膨胀桥接断裂的缝隙
I = imread('starcraft.bmp');
Ie1 = imerode(I,[1 1 1;1 1 1;1 1 1]);
Ie2 = imerode(Ie1,[0 1 0;1 1 1;0 1 0]);
Id1 = imdilate(Ie2,[1 1 1;1 1 1;1 1 1]);
Id2 = imdilate(Id1,[0 1 0;1 1 1;0 1 0]);
figure;
subplot(2,2,1);
imshow(Ie1);
subplot(2,2,2);
imshow(Ie2);
subplot(2,2,3);
imshow(Id1);
subplot(2,2,4);
imshow(Id2);
开运算及其实现
开运算和闭运算都由腐蚀和膨胀复合而成, 开运算是先腐蚀后膨胀, 而闭运算是先膨胀后腐蚀。
一般来说, 开运算可以使图像的轮廓变得光滑, 还能使狭窄的连接断开和消除细毛刺。
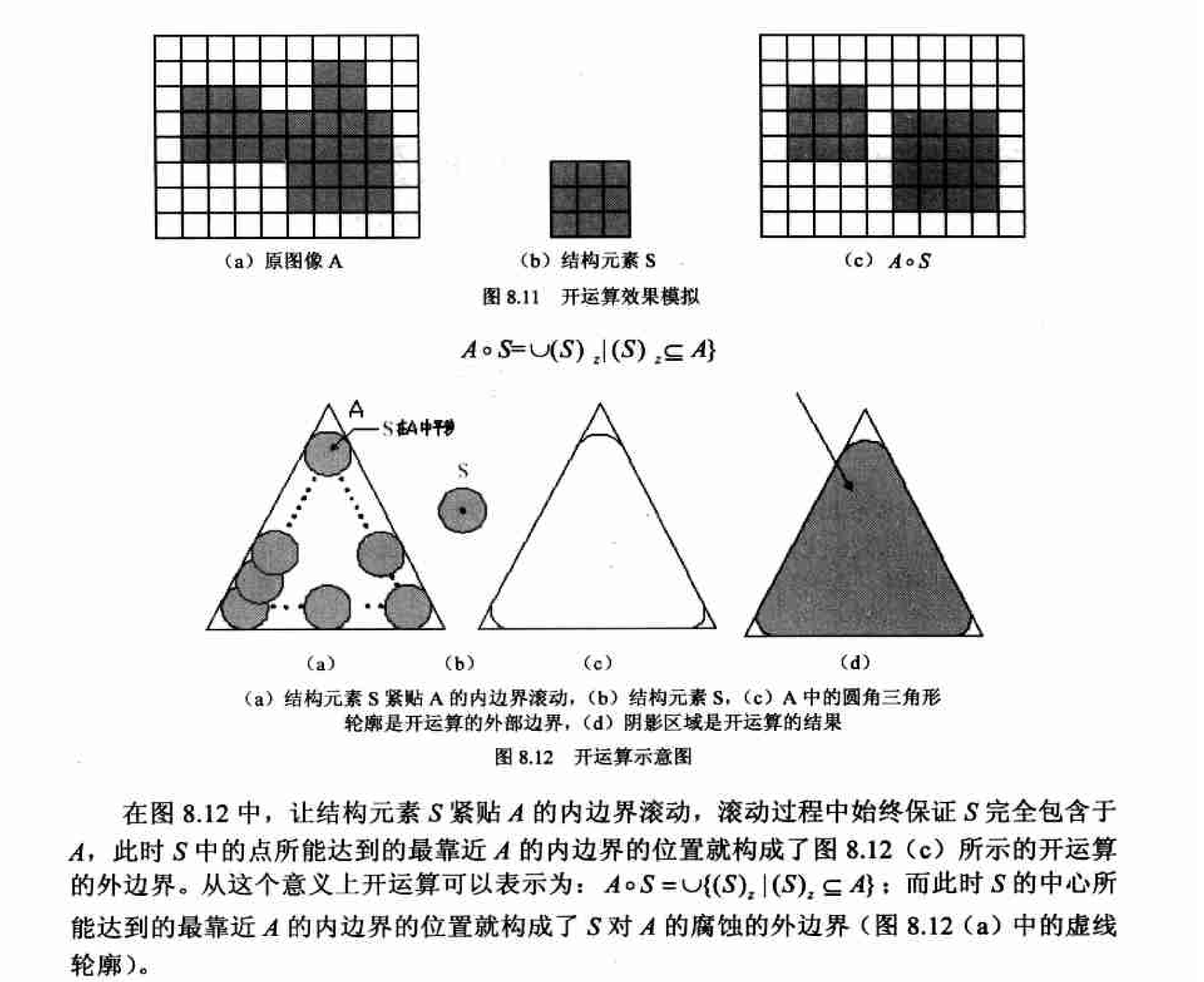
如图8.11所示, 开运算断开了团中两个小区域间两个像素宽的连接〈断开了狭窄连接〉,并且去除了右侧物体上部突出的一个小于结构元素的2×2的区域〈去除细小毛刺〉: 但与腐蚀不同的是, 图像大的轮廓并没有发生整体的收缩, 物体位置也没有发生任何变化。
根据图8.12 的开运算示意图, 可以帮助大家更好地理解开运算的特点。为了比较, 图中也标示出了相应的腐蚀运算的结果:
matlab实现
根据定义,以相同的结构元素先后调用imerode和imdilate即可实现开操作。此外,Matlab 中也直接提供了开运算函数imopen, 其调用形式如下:
I2 = imopen(I,SE);
I = imread('erode_dilate.bmp');
Io = imopen(I,ones(6,6));
figure;
subplot(1,2,1);
imshow(I);
subplot(1,2,2);
imshow(Io);
从图8.13中可以看到同腐蚀相比,开运算在过滤噪声的同时并没有对物体的形状、轮廓造成明显的影响,这是一大优势。但当我们只关心物体的位置或者个数时,物体形状的改变不会给我们带来困扰,此时用腐蚀滤波具有处理速度上的优势〈同开运算相比节省了一次膨胀运算〉。
闭运算及其实现
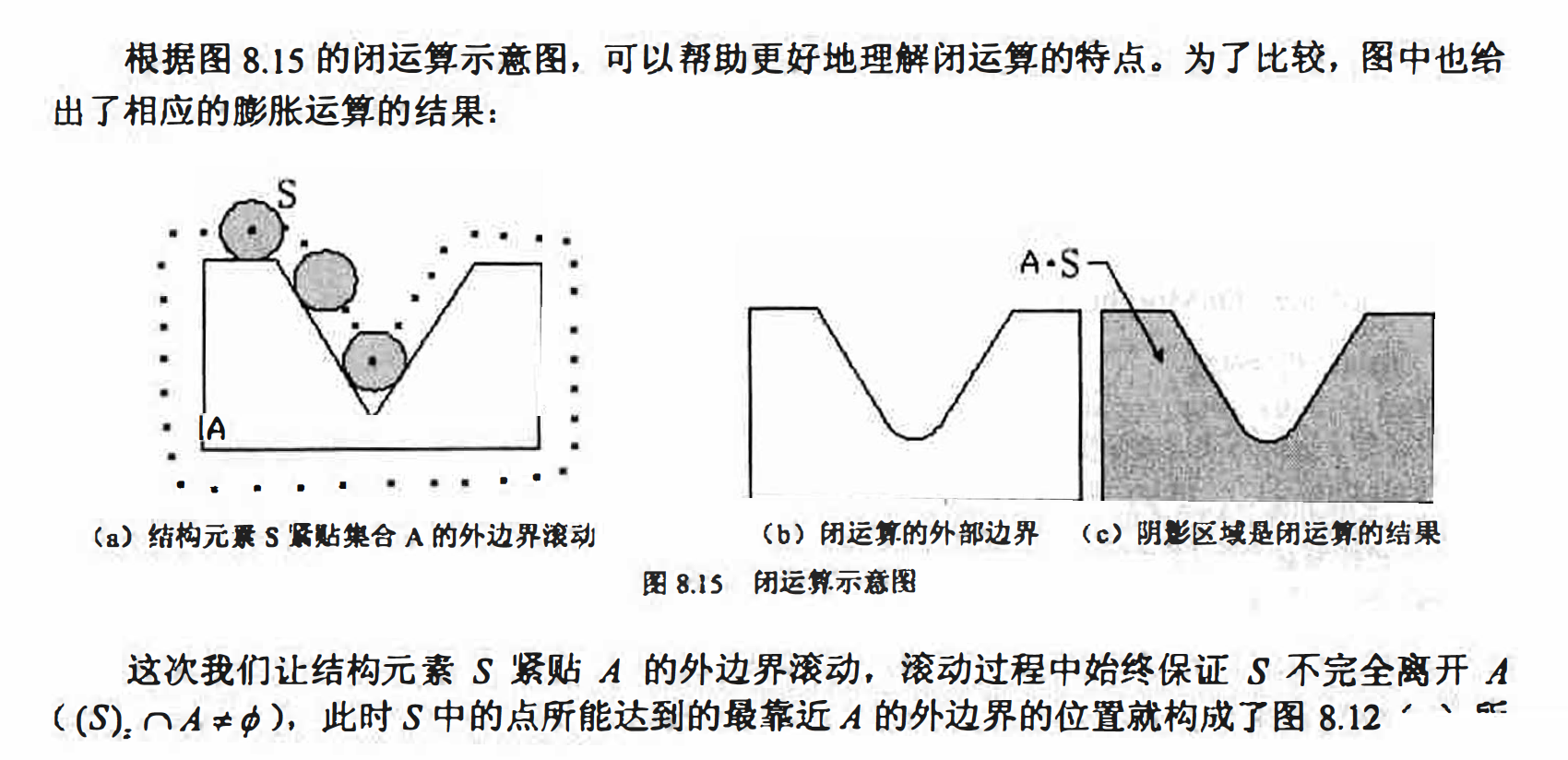
闭运算同样可以使轮廓变得光滑, 但与开运算相反, 它通常能够弥合狭窄的间断, 填充小的孔洞。

Matlab实现
根据定义,以相同的结构元素先后调用imdilate 和imerode 即可实现闭操作。此外,Matlab中也直接提供了闭运算函数imclose, 其用法同imopen 类似
二值图像中的形态学应用
击中与击不中交换及其实现

I = zeros(120,180);
I(11:80,16:75)=1;
I(56:105,86:135)=1;
I(26:55,141:170)=1;
se = zeros(58,58);
se(5:54,5:54)=1;
Ie1 = imerode(I,se);
Ic = 1 - I;
S2 = 1 - se;
Ie2 = imerode(Ic,S2);
Ihm = Ie1&Ie2;
figure;
subplot(2,2,1);
imshow(I);
subplot(2,2,2);
imshow(Ie1);
subplot(2,2,3);
imshow(Ie2);
subplot(2,2,4);
imshow(Ihm);
图中给出了变换的最终结果。为便于观察在显示时每幅图像周围都环绕着一圈黑色边框, 注意该边框并不是图像本身的一部分。
注意: 注意对于结构元素s,我们感兴趣的物体S1之外的背景S2不能选择得太宽,因为使得S包含背景S2的目的仅仅是定义出物体S1的外轮廓,以便在图像中能够
找到准确的完全匹配位置. 从这个意义上说, 物体S1周围有一个像素宽的背景环绕就足够了, 例8.3中选择了4个像素宽的背景,是为了使结构元素背景部分应
看起来比较明显, 但如果背景部分过大, 则会影响击中/击不中变换的计算结果.在上例中, 中间的正方形Y与右上的正方形Z之间的水平距离为6,如果在定义S时, S2的宽度超过6个像素, 则最终的计算结果将是空集.

边界提取与跟踪及其实现
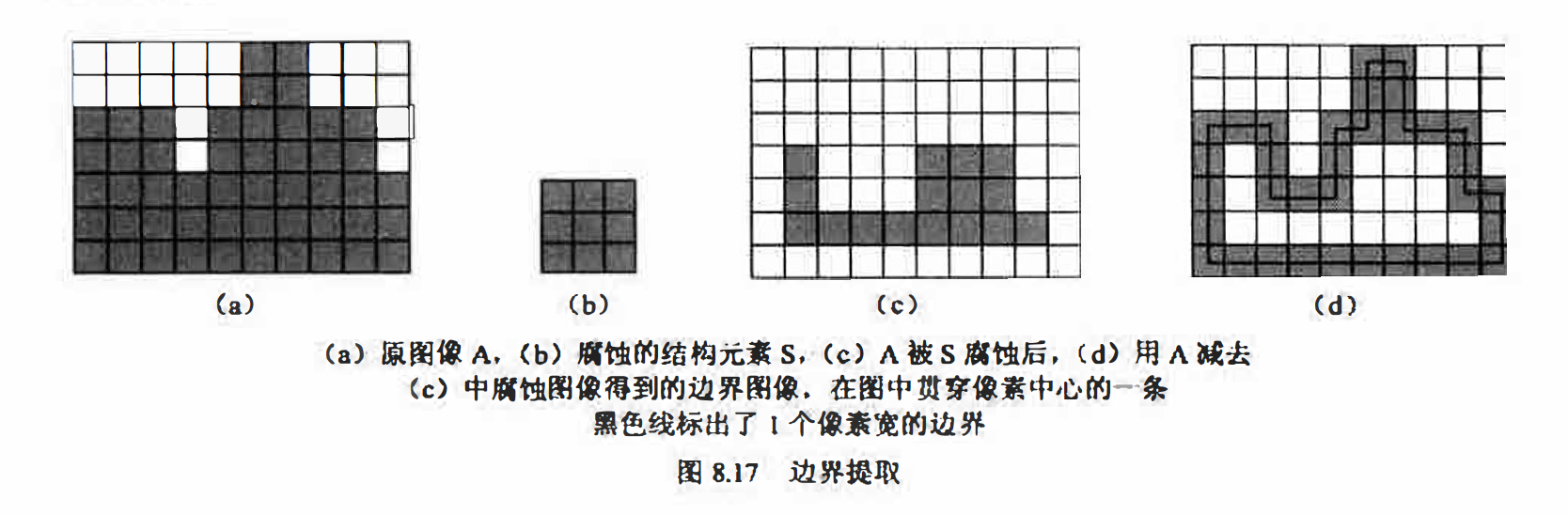
轮廓是对物体形状的有力描述, 对图像分析和识别十分有用。通过边界提取算法可以得到物体的边界轮廓:而边界跟踪算法在提取边界的同时还能依次记录下边界像素的位置信息,下面分别介绍.
边界提取
要在二值图像中提取物体的边界,容易想到的一个方法是将所有物体内部的点删除(置为背景色〉。具体地说,可以逐行扫描原图像,如果发现一个黑点〈图8.17 中黑点为前景点)的8个邻域都是黑点, 则该点为内部点, 在目标图像中将它删除。实际上这相当于采用一个3*3的结构元素对原图像进行腐蚀, 使得只有那些8个邻域都有黑点的内部点被保留,再用原图像减去腐蚀后的图像, 恰好删除了这些内部点, 留下了边界像素。这一过程可参
见图8.17 。
I = imread('head_portrait.bmp');
se = strel('square',3);
Ie = imerode(I,se);
Iout = I - Ie;
figure;
subplot(1,2,1);
imshow(I);
subplot(1,2,2);
imshow(Iout);
边界跟踪

区域填充
区域填充可视为边界提取的反过程, 它是在边界已知的情况下得到边界包围的整个区域的形态学技术。
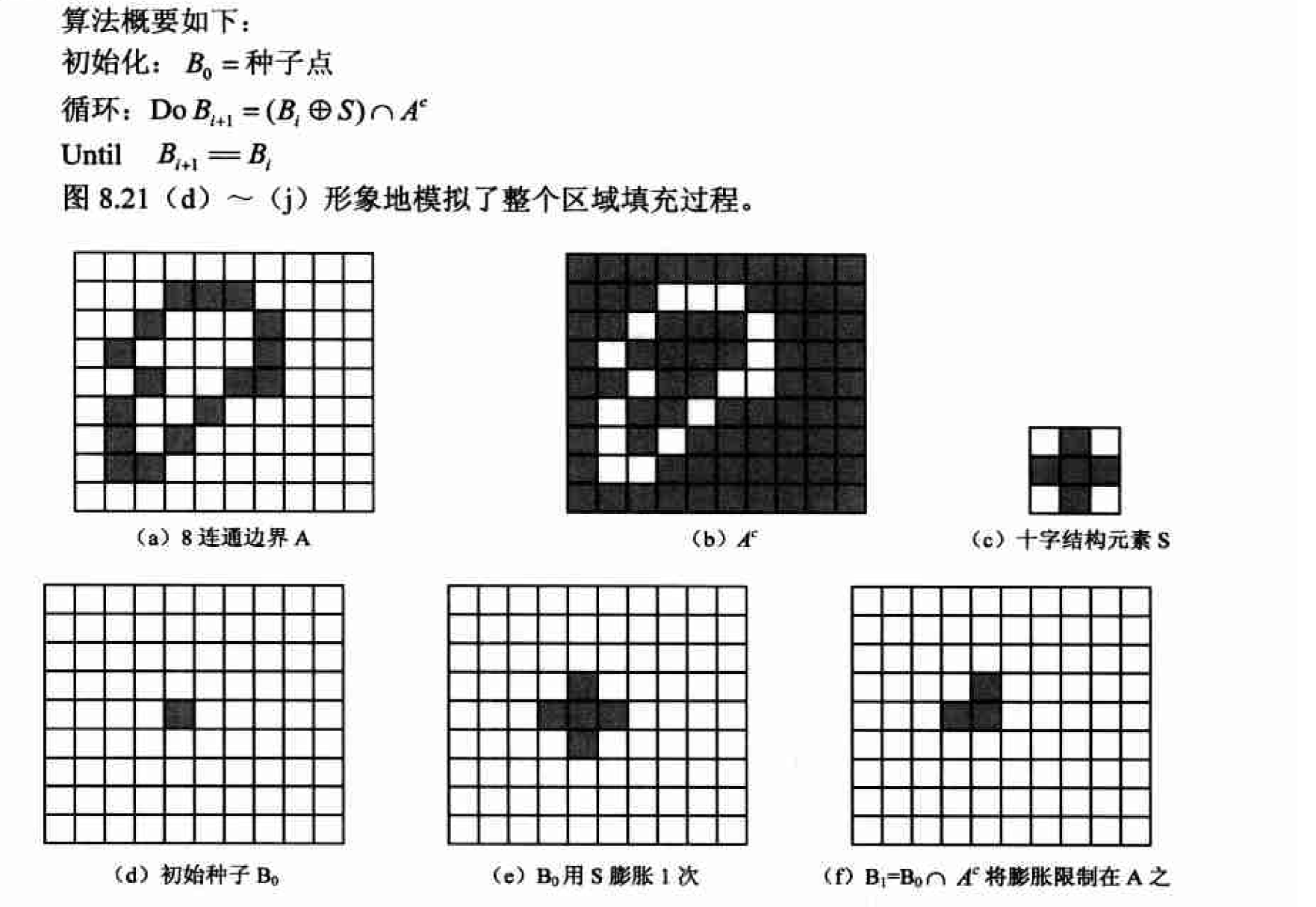
理论基础
问题的描述如下: 己知某-8连通边界和边界内部的某个点, 要求从该点开始填充整个边界包围的区域, 这一过程称为种子填充, 填充的开始点被称为种子.
如图8.20 所示, 对于4 连通的边界, 其围成的内部区域是8 连通的, 而8连通的边界围成的内部区域却是4连通的.
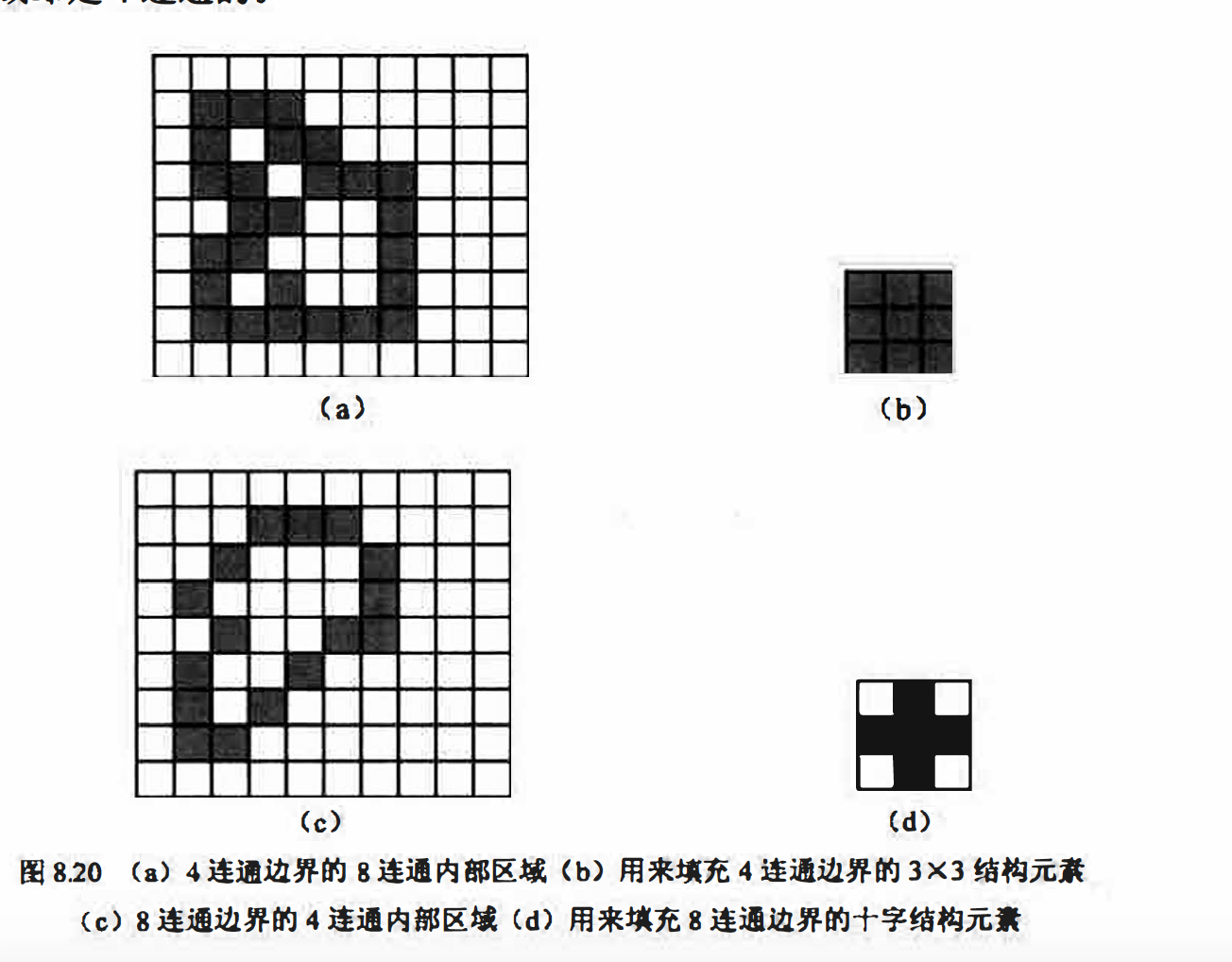
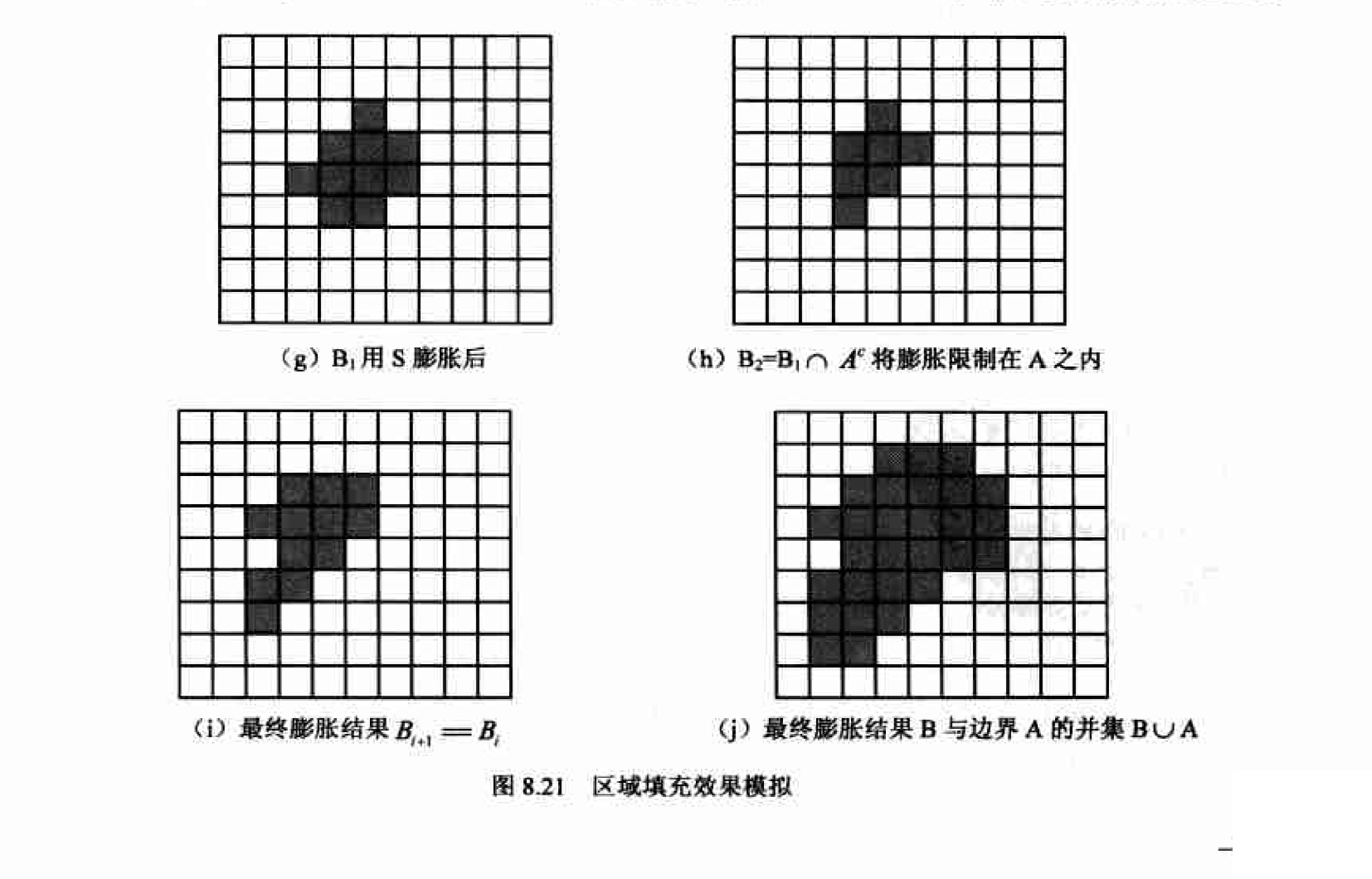
为了填充4 连通的边界应选择图8.20 (b )中的3 × 3 结构元素, 但如果想在8 连通边界内从种子点得到区域则需选用图8.20 (d)的十字结构元素S 对初始时仅为种子点的图像B进行膨胀,十字结构元素S能够保证只要B在边界A的内部〈不包括边界本身〉,每次膨胀都不会产生边界之外的点(新膨胀出来的点或者在边界内部, 或者落在边界上〉, 这样只需把每次膨胀的结果图像和边界的补图像
不断膨胀, B的区域不断生长, 但每次膨胀后与
连通分量提取及其实现
连通分量的概念在0.3.1小节中曾介绍过。在二值图像中提取连通分量是许多自动图像分析应用中的核心任务。提取连通分量的过程实际上也是标注连通分量的过程, 通常的做法是给原图像中的每个连通区分配一个唯一代表该区域的编号, 在输出图像中该连通区内的所有像素的像素值就赋值为该区域的编号, 我们将这样的输出图像称为标注图像。

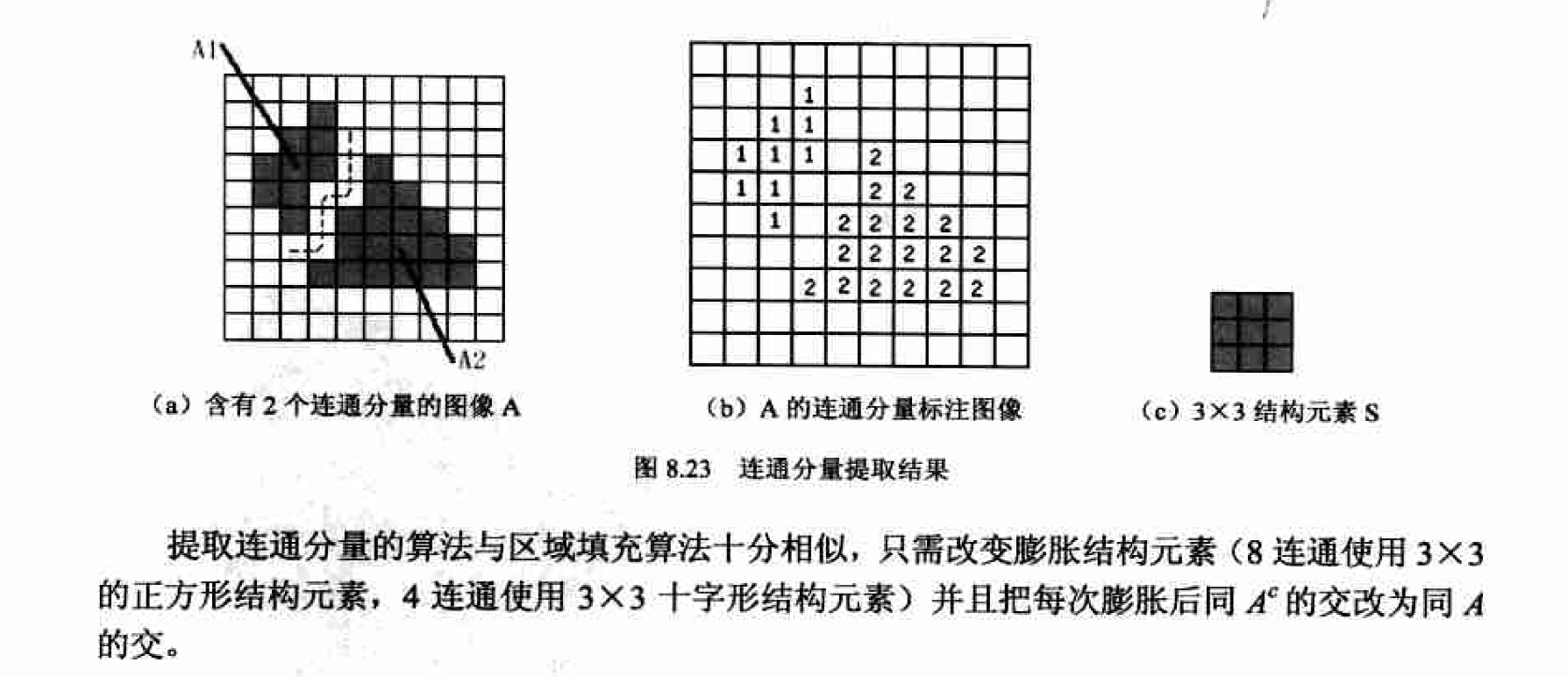
matlab实现
在Matlab中, 连通分量的相关操作主要借助IPT函数bwlabel实现. 其调用语法为
[L num]= bwlabel(Ibw,conn);
Ibw为一幅输入二位图像.
conn为可选参数, 指明要提取的连通分量是4连边还是8连通, 默认值为8.
L为类似于图8.23 ( b)的标注图像.
num为二维图像Ibw中连通分量的个数.
提取连通分量的应用十分广泛, 利用标注图像可以方便地进行很多基于连通区的操作。例如要计算某一连通分量的大小, 只需扫描一遍标注图像, 对像素值为该区编号的像素进行计数: 又如要计算某一连通分量的质心, 只需扫描一遍标注图像, 找出所有像素值为该区编号的像素的x、y坐标, 然后计算其平均值.
在人脸局部图像中定位嘴的中心
我们希望在如图8.24 (a )所示的图像中定位嘴的中心,假定已经掌握了输入图像中的某些先验知识,嘴部占据了图像的大部分区域且从灰度上易于与周围皮肤分离开来. 于是针
对性地拟定了在二位化图像中寻找最大连通区域中心的解决方案, 具体步骤为:
(1)对输入图像进行二位化处理.
(2)标注二值图像中的连通分量.
(3)找出最大的连通分量.
(4)计算最大连通分量的中心.
% locateMouth.m
I = imread('mouth.bmp'); %读入图像
Id = im2double(I);
figure, imshow(Id) % 得到8.24(a)
Ibw = im2bw(Id, 0.38); % 以0.38为阈值二值化
Ibw = 1 - Ibw; %为在Matlab中进行处理,将图像反色
figure, imshow(Ibw) % 得到8.24(b)
hold on
[L, num] = bwlabel(Ibw, 8); % 标注连通分量
disp(['图中共有' num2str(num) '个连通分量'])
% 找出最大的连通分量(嘴)
max = 0; % 当前最大连通分量的大小
indMax = 0; % 当前最大连通分量的索引
for k = 1:num
[y x] = find(L == k); % 找出编号为k的连通区的行索引集合y和列索引集合x
nSize = length(y); %计算该连通区中的像素数目
if(nSize > max)
max = nSize;
indMax = k;
end
end
if indMax == 0
disp('没有找到连通分量')
return
end
% 计算并显示最大连通分量(嘴)的中心
[y x] = find(L == indMax);
yMean = mean(y);
xMean = mean(x);
plot(xMean, yMean, 'Marker', 'o', 'MarkerSize', 14, 'MarkerEdgeColor', 'w', 'MarkerFaceColor', 'w');
plot(xMean, yMean, 'Marker', '*', 'MarkerSize', 12, 'MarkerEdgeColor', 'k'); % 得到8.24(c)细菌计数
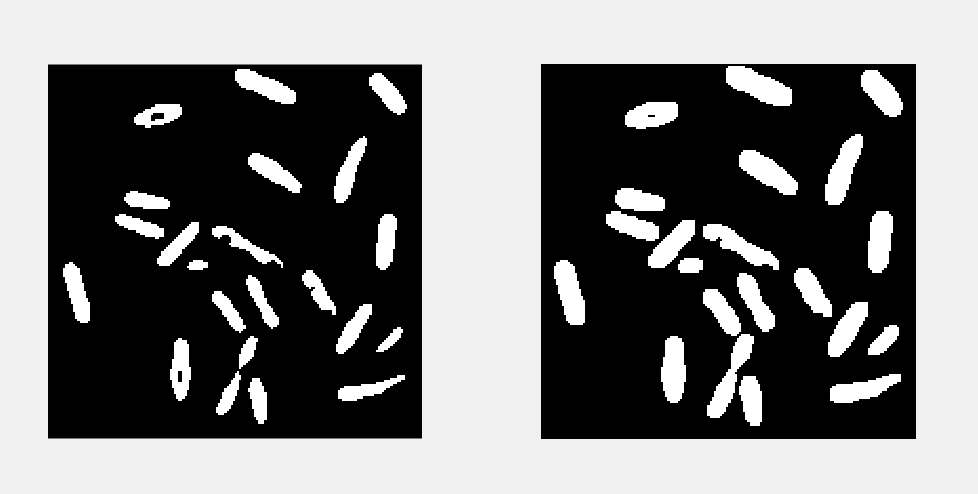
I = imread('bw_bacteria.bmp');
[L,num]=bwlabel(I,8);
Idil = imdilate(I,ones(3,3));
[L,num] = bwlabel(Idil,8);
figure;
subplot(1,2,1);
imshow(I);
subplot(1,2,2);
imshow(Idil);