机器学习中的线性代数

线性代数选讲

• 线性代数和矩阵
  线性空间和几何的关系
  线性空间是一些向量的几何, 可以做加减, 分配率等操作
  
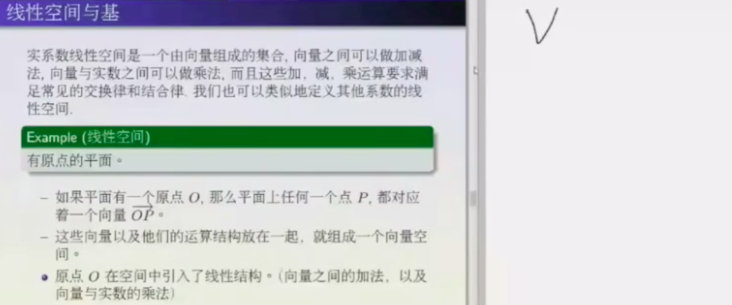
  如何做计算?
  基是线性空间里的一组向量, 使得任何一个向量可以唯一的表示成这组向量的线性组合.
  有了基, 向量就可以表示成一个点(a, b)
  

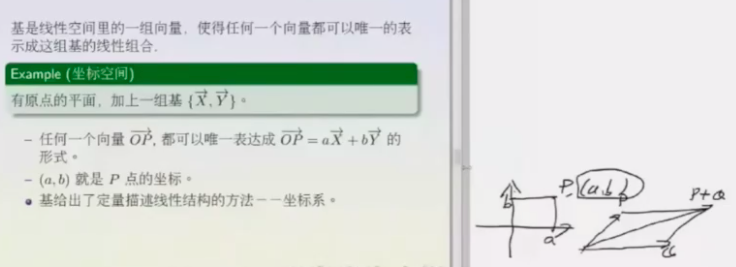
• 矩阵变换和特征值
  线性变换就引入了矩阵,
  
  
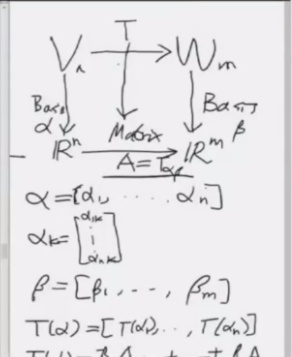
  从低维空间到高位空间的映射, 因为 a 是一个基, b 是一个基, 因此如果有一个映射函数 T, 那么就存在 T(a) = bA
  
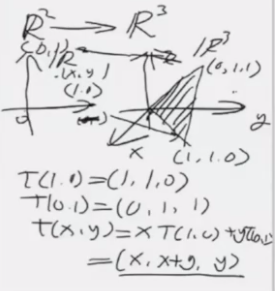
  同样也可以进行高维对低微的映射, 把平面压成一条线, 类似于投影
  
  
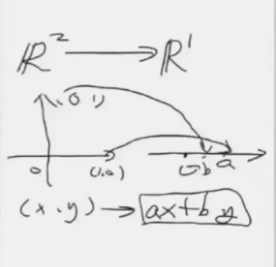
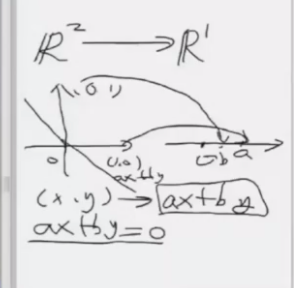
  对于不同的基, 进行变换, 这两个矩阵是存在关系的
  
  
  不同的基得到不同的矩阵

• 分类理论
  相似变换, 行列式, 相似变化下, 行列式是不变的, 迹也是不变的,秩也是不变的 特征值也是不变的, 为什么求特征值
  
  
  相似不变量的最重要的量是特征值
  

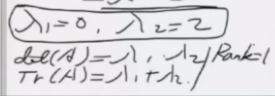
• 二次型
  二次型是一个度量, 这样可以求任何基下面的度量(长度)
  
  两个矩阵描述同一个度量
  
  

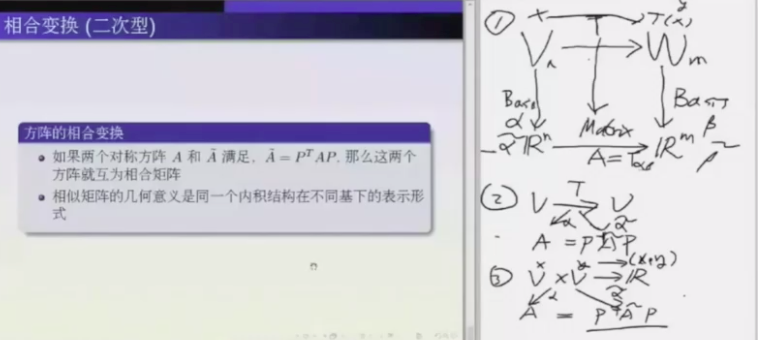
• 正交相似的标准型
  

• 奇异值分解
  

• 应用举例:PCA
  当数据维度很大的时候, 如果我们相信大部分的变量之间存在线性关系,那么我们相信降低维数,用较少的变量来抓住大部分的信息
  
  

• 参考资料