文献翻译,有疑问欢迎大家讨论。
主要工作
使用混合灵敏度H∞分析(mixed-sensitivith H∞ synthesis)设计ANC中的反馈滤波器,考虑次级通路建模的不确定性和闭环系统的稳定性。这种方法在拉普拉斯域和z变换域进行分析,对频域中的现象有更直观的解释。
背景
对于ANC反馈系统中的啸叫问题有理论参考性。
理论
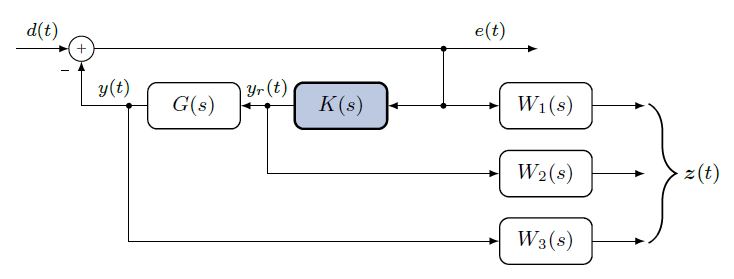
图中W1、W2和W3是加权方程,是频散的,可以根据设计目的对W1/W2/W3进行调控。
先定义灵敏度:
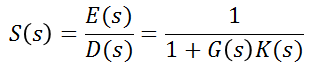
灵敏度是误差信号与输入信号之比,量化了系统对误差扰动和参数变化的敏感度。在ANC中反映降噪能力。
定义互补灵敏度:
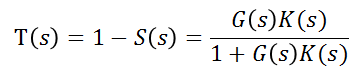
描述了对测量误差n的相应,在图中没有给出。
反馈系统的总误差为:
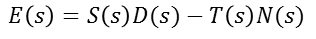
理论上,S(s)和T(s)两个灵敏度都应该比较小,系统才稳定。但是由于两者之和为1,所以需要在两个灵敏度之间平衡。
设计目标函数,求使目标函数最小时的反馈滤波器K
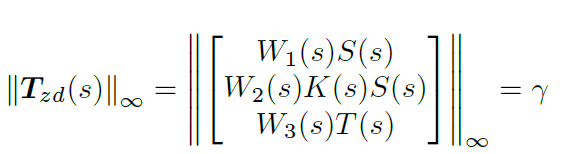
上式中都是SISO(单输入单输出)的在Lapace域的传函。
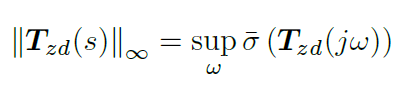
上式代表最大奇异值的最大绝对值。
其中
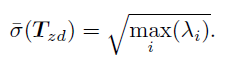
设计反馈滤波器
W1/W2/W3可以影响最后求得的滤波器K,一般W1是与扰动信号带宽相近的低通滤波器,W2一般设置成0,W3交叉频率在期望闭环系统带宽的高通滤波器。
然而,并不能对灵敏度做任意形状的改变,Bode灵敏度积分就对其有所限制,大概意思是对某频带灵敏度的下压,就必然导致其他频带的抬高。
尽管有这样的限制,我们还是可以利用混合灵敏度优化来设计鲁棒性稳定的滤波器。
次级通路影响
用扫频信号实测次级通路,得到离散的次级通路G(z)。用线性插值得到Laplace域的连续G(s),使用16阶。
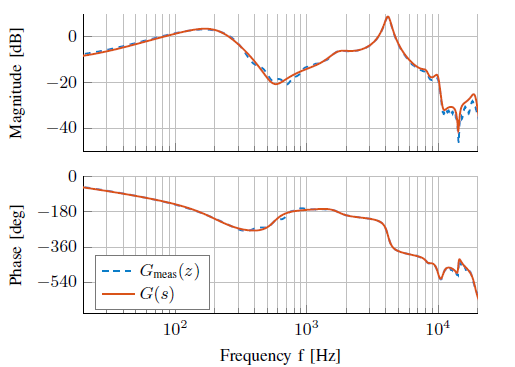
在ANC中,耳机的塞紧程度、耳道的容积和耳机的材料都会对次级通道产生影响。
对有扰动的G(s)建模:
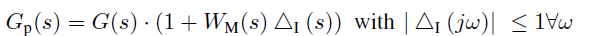
WM是G(s)变化的上限。
如果要保证系统在所有实际情况下都稳定,需要满足以下要求:
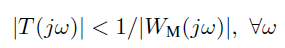
对不同佩戴方式,从完全松到完全紧,进行测量,计算WM
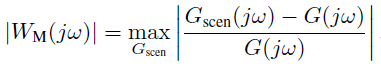
加权函数W3可以任意选择,但是不应低于WM。
如下图所示,由于观察到的小型驻极体麦克风的典型测量误差,我们增加了W3内对于30 Hz以下的低频和10 kHz以上的频率的不确定性,W3有20阶。

此外,由于我们希望滤波器在高频范围内具有广泛的增益,因此分两步提高了700 Hz和10 kHz之间的不确定性。(不太明白这个设计)
具体设计
假设目标函数中γ=1,则滤波器系数应满足:
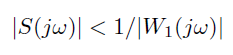

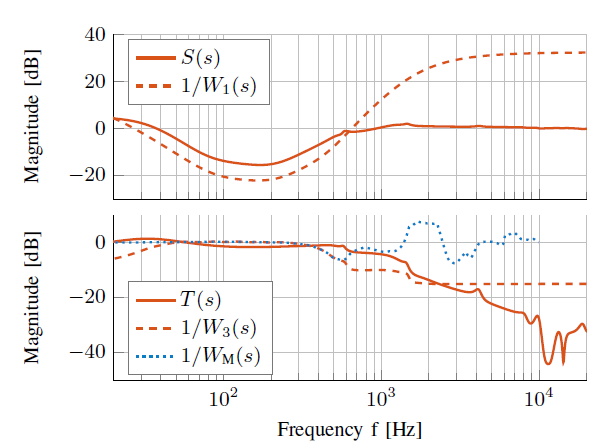
S(s)和1/W1的图可能画反了。
结果
最后设计出的降噪曲线。

评价
可以通过S(s)来判断反馈系统是否有啸叫,对反馈滤波器K(s)进行相应改进。
不过这个降噪效果感觉有待加强。