- 监督学习
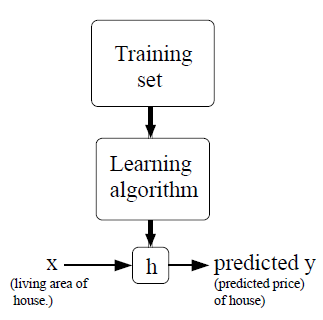
如上图所示,监督学习:对于给定的训练集合,按照某一学习算法学习之后,得到一种好的假设(Hypotheses)用于预测新的数据。
- 梯度下降
已知m组数据(x1,y1)…(xm, ym),其中xi是具有n维特征的向量,此外,我们设定xi(0) =1(即截距项)。我们做如下假设:
h(x) = = (此为回归模型的假设模型)
对于给定的训练集合,如何选择最优的θ值(权重或参数)呢(这里的x是n+1*m维矩阵)?一个合理的方法是:至少在训练集合上,θ会使预测值h(x)越接近实际值y越好。因此,我们定义一个成本函数(cost function) J(θ):
该成本函数使用误差的平方和,类似于普通最小二乘法(没有平均化误差平方和)。
-
最小均方算法
给定的训练集合,如何选择最优的θ值使J(θ)?这里我们采用梯度下降法。梯度下降法的基本思想是在起始随机得到θ值后,之后每次更新θ值的方式如下:
即θ每次以一定的步伐按照J(θ)最快速下降的方向更新值。我们进一步分解参数更新公式的右边。
= = *
= (h(x)-y) * = (h(x)-y)*xi
因此,参数更新的方式如下:
该更新方法称之为LMS算法(least mean squares,最小均方法),也被称为Widrow-Hoff 学习算法。该方法显得很自然和直观化。比如,当误差(y-h(x))越大的时候,那么参数更新的步伐就越大。检测是否收敛的方法:1) 检测两次迭代θj的改变量,若不再变化,则判定收敛;2) 更常用的方法:检验J(θ),若不再变化,判定收敛。需要注意的是,学习系数一般为0.01或者0.005等,我们可以发现样本量越大,(y-h(xi))*xji会相对较大,所以在学习系数中用一个常数除以样本来定相对合理,即0.005/m。
对于LMS算法,刚才推导的公式是针对于一个样本,如果样本多于一个,那么我们可以有两种方式更新参数。一种是每一次更新都使用全部的训练集合,该方法称之为批量梯度下降(batch gradient descent)。需要注意的是,梯度下降法很可能得到局部最优解,而我们这里的回归分析模型仅有一个最优解,因此局部最优解就是最终的最优解。(成本函数为凸函数)。另外一种是针对训练集合中每一个样本,每次都更新所有的参数值,该方法称之为随机梯度下降(stochastic gradient descent)。当数据量很大的时候,批量梯度下降法计算量较大,而随机梯度下降方法往往相对较优。通常情况下,随机梯度下降比批量梯度下降能更快的接近最优值(但也许永远也得不到最优值),数据量大的情况下,通常选择使用随机梯度下降法。
梯度下降法的缺点是:靠近极小值时速度减慢(极小值处梯度为0),直线搜索可能会产生一些问题(得到局部最优等),可能会'之字型'地下降(学习速率太大导致)。
-
标准方程组推导
最小化成本函数的方式不只是有梯度下降法,这里我们采用标准方程组的方式求解得到精确的解。对于成本函数J(θ) ,我们定义输入变量X是m*(n+1)维矩阵(包含了截距项),其中m表示样本数,n表示特征数。输出是m*1维矩阵,参数θ是n+1*1维矩阵,则J(θ)可以如下表示:
J(θ) = (Xθ – )T * (Xθ-)
要求解θ使得J(θ)最小,那么只需要求解J(θ)对θ的偏微分方程即可。
∇θJ(θ) = [(Xθ – )T * (Xθ-)]
= T]*(Xθ – ) + (Xθ – )T ]*
= XT*(Xθ – ) + XT*(Xθ – )
= XT*(Xθ – )
= XT*X*θ – XT*
因此,令∇θJ(θ) = 0,即可求得使J(θ)最小的θ的值,因此:XT*X*θ – XT* = 0,得到 θ = (XT*X)-1 * (XT*)。在求解回归问题时候,可以直接使用该结果赋值于θ,不过这里存在的问题是对矩阵的求逆,该过程计算量较大,因此在训练集合样本较大的情况并不适合。
注:∇θJ(θ)表示对J(θ)中的每一个θ参数求偏微分。这里化简的方式是矩阵偏微分注意:AT*B) = BT)*A, AT = (A)T, AT*B = (BT*A)T。
-
概率解释
对于回归问题,我们不禁要问为什么线性回归或者说为什么最小均方法是一个合理的选择呢?这里我们通过一系列的概率假设给出一个解释。(下一讲)