一 基础知识梳理:
并查集(Union-find Sets)是一种非常精巧而实用的数据结构,它主要用于处理一些不相交集合的合并问题。一些常见的用途有求连通子图、求最小生成树的 Kruskal 算法和求最近公共祖先(Least Common Ancestors, LCA)等。
使用并查集时,首先会存在一组不相交的动态集合 S={S1,S2,⋯,Sk},一般都会使用一个整数表示集合中的一个元素。
每个集合可能包含一个或多个元素,并选出集合中的某个元素作为代表。每个集合中具体包含了哪些元素是不关心的,具体选择哪个元素作为代表一般也是不关心的。我们关心的是,对于给定的元素,可以很快的找到这个元素所在的集合(的代表),以及合并两个元素所在的集合,而且这些操作的时间复杂度都是常数级的。
并查集的基本操作有三个:
- makeSet(s):建立一个新的并查集,其中包含 s 个单元素集合。
- unionSet(x, y):把元素 x 和元素 y 所在的集合合并,要求 x 和 y 所在的集合不相交,如果相交则不合并。
- find(x):找到元素 x 所在的集合的代表,该操作也可以用于判断两个元素是否位于同一个集合,只要将它们各自的代表比较一下就可以了。
并查集的实现原理也比较简单,就是使用树来表示集合,树的每个节点就表示集合中的一个元素,树根对应的元素就是该集合的代表,如图 1 所示。

图 1 并查集的树表示
图中有两棵树,分别对应两个集合,其中第一个集合为 {a,b,c,d},代表元素是 a;第二个集合为 {e,f,g},代表元素是 e。
树的节点表示集合中的元素,指针表示指向父节点的指针,根节点的指针指向自己,表示其没有父节点。沿着每个节点的父节点不断向上查找,最终就可以找到该树的根节点,即该集合的代表元素。
现在,应该可以很容易的写出 makeSet 和 find 的代码了,假设使用一个足够长的数组来存储树节点(很类似之前讲到的静态链表),那么 makeSet 要做的就是构造出如图 2 的森林,其中每个元素都是一个单元素集合,即父节点是其自身:

图 2 构造并查集初始化
相应的代码如下所示,时间复杂度是 O(n):
1 #define maxn 500 2 int uset[maxn]; 3 void makeset(int size) 4 { 5 for(int i=0;i<size;i++)//初始化,把所有点的父节点定为自身 6 uset[i]=i; 7 }
接下来,就是 find 操作了,如果每次都沿着父节点向上查找,那时间复杂度就是树的高度,完全不可能达到常数级。这里需要应用一种非常简单而有效的策略——路径压缩。
路径压缩,就是在每次查找时,令查找路径上的每个节点都直接指向根节点,如图 3 所示。

我准备了两个版本的 find 操作实现,分别是递归版和非递归版,不过两个版本目前并没有发现有什么明显的效率差距,所以具体使用哪个完全凭个人喜好了。
下面展示两种形式的代码:
1 int find(int x) 2 { 3 if(x==uset[x]) return x;//如果是父节点,则返回自身的值 4 else if(x!=uset(x)) uset[x]=find(uset[x]);//否则递归调用直到根节点 5 return uset[x];//最后根节点的值在uset[x]中 6 }
1 int find(int x) 2 { 3 int p=x,t; 4 while(p!=uset[p]) p=uset[p];//首先找到根节点 5 while(x!=p)//路径压缩过程 6 { 7 t=uset[x];//把x自身的相邻父节点赋值给t 8 uset[x]=p;//把x的父节点改为p 9 x=t;//移动到相邻父节点,然后处理之 10 }
最后是合并操作 unionSet,并查集的合并也非常简单,就是将一个集合的树根指向另一个集合的树根,如图 4 所示。
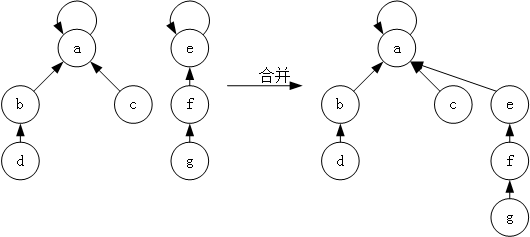
图 4 并查集的合并
这里也可以应用一个简单的启发式策略——按秩合并。该方法使用秩来表示树高度的上界,在合并时,总是将具有较小秩的树根指向具有较大秩的树根。简单的说,就是总是将比较矮的树作为子树,添加到较高的树中。为了保存秩,需要额外使用一个与 uset 同长度的数组,并将所有元素都初始化为 0。
void unionSet(int x, int y) { if ((x = find(x)) == (y = find(y))) return;//如果是同一个父节点,则直接返回 if (rank[x] > rank[y]) uset[y] = x;//把秩较小的y子树赋值给较大的子树x else { uset[x] = y;//把秩较小的x子树并在y子树上 if (rank[x] == rank[y]) rank[y]++;//如果两棵子树大小相同,则把树的大小加1 } }
下面是按秩合并的并查集的完整代码,这里只包含了递归的 find 操作。
const int MAXSIZE = 500; int uset[MAXSIZE]; int rank[MAXSIZE]; void makeSet(int size) { for(int i = 0;i < size;i++) uset[i] = i; for(int i = 0;i < size;i++) rank[i] = 0;//开始时树的高度为0 } int find(int x) { if (x != uset[x]) uset[x] = find(uset[x]); return uset[x]; } void unionSet(int x, int y) { if ((x = find(x)) == (y = find(y))) return; if (rank[x] > rank[y]) uset[y] = x; else { uset[x] = y; if (rank[x] == rank[y]) rank[y]++; } }
除了按秩合并,并查集还有一种常见的策略,就是按集合中包含的元素个数(或者说树中的节点数)合并,将包含节点较少的树根,指向包含节点较多的树根。这个策略与按秩合并的策略类似,同样可以提升并查集的运行速度,而且省去了额外的 rank 数组。
这样的并查集具有一个略微不同的定义,即若 uset 的值是正数,则表示该元素的父节点(的索引);若是负数,则表示该元素是所在集合的代表(即树根),而且值的相反数即为集合中的元素个数。相应的代码如下所示,同样包含递归和非递归的 find 操作: 1constint MAXSIZE = 500 2 int uset[MAXSIZE];
3 4 void makeSet(int size) { 5 for(int i = 0;i < size;i++) uset[i] = -1;//初始节点数为1,所以赋值为-1 6 } 7 int find(int x) { 8 if (uset[x] < 0) return x; 9 uset[x] = find(uset[x]); 10 return uset[x]; 11 } 12 int find(int x)
{ 13 int p = x, t; 14 while (uset[p] >= 0) p = uset[p]; 15 while (x != p) { 16 t = uset[x]; 17 uset[x] = p; 18 x = t; 19 } 20 return x; 21 }
void unionSet(int x, int y) { if ((x = find(x)) == (y = find(y))) return; if (uset[x] < uset[y]) { //注意这里值越小,所代表的节点数越多,因为是用的负值表示的节点数 uset[x] += uset[y]; uset[y] = x; } else { uset[y] += uset[x]; uset[x] = y; } }
如果要获取某个元素 x 所在集合包含的元素个数,可以使用 -uset[find(x)] 得到。
并查集的空间复杂度是 O(n) 的,这个很显然,如果是按秩合并的,占的空间要多一些。find 和 unionSet 操作都可以看成是常数级的,或者准确来说,在一个包含 n 个元素的并查集中,进行 m 次查找或合并操作,最坏情况下所需的时间为 O(mα(n)),这里的 α 是 Ackerman 函数的某个反函数,在极大的范围内(比可观察到的宇宙中估计的原子数量 1080 还大很多)都可以认为是不大于 4 的。具体的时间复杂度分析,请参见《算法导论》的 21.4 节 带路径压缩的按秩合并的分析。
二 解题思路:
1 #include<iostream> 2 using namespace std; 3 #define maxn 30005 4 int fa[maxn]; 5 int ans[maxn]; 6 int find(int x) 7 { 8 return fa[x]==x?x:fa[x]=find(find[x]); 9 } 10 int main() 11 { 12 int t; 13 cin>>t; 14 while(t--) 15 { 16 for(int i=0;i<maxn;i++) 17 {fa[i]=i;ans[i]=0;} 18 int n,m,x,y,u,v; 19 cin>>n>>m; 20 for(int j=1;j<=m;j++) 21 { 22 cin>>x>>y; 23 u=find(x);//寻找各自的跟节点 24 v=find(y);//寻找各自的跟节点 25 if(u!=v)//父节点不相同 26 fa[u]=v;//把x的根节点的父节点指为y的根节点 27 } 28 for(int i=0;i<n;i++) 29 ans[find(i)]++;//求各个子树的节点最大数目 30 int a=0; 31 for(int i=0;i<n;i++) 32 if(a<ans[i]) a=ans[i]; 33 cout<<a<<endl; 34 } 35 return 0; 36 }
在做这个题目时,我自己一开始的想法是运用BFS,自己还写出了代码。但是运用BFS的最大缺陷是所开的空间太大(邻接矩阵的边长最大为30005)。这样会使空间存储不下。所以在用BFS解题的时候一定要注意数据不能过大。下面是自己写的代码,可以看看如何运用BFS解决相关问题:
#include<iostream> #include<algorithm> #include<string.h> using namespace std; #define maxn 30005 //数据过大 int q[maxn]; int n,m; int map[maxn][maxn]; void input() { memset(map,0,sizeof(map)); int n1,m1; for(int i=1;i<=m;i++)//输入数据并赋值给邻接矩阵 { cin>>n1>>m1; map[n1][m1]=1; map[m1][n1]=1; } } int bfs(int k) { int front,rear; front=rear=0; q[rear++]=k; while(front<rear) { int u=q[front++]; for(int i=1;i<=m;i++) { if(map[u][i])//判断是否能够入队,能够入队就入队 { int judge=0; for(int k=0;k<rear;k++)//找队列里面是否原来就有该元素
if(i==q[k]) {judge=1;break;} if(!judge) q[rear++]=i; } } } return rear; } int main() { int t; cin>>t; while(t--) { cin>>n>>m; input(); int num=0; for(int i=1;i<=n;i++) { memset(q,0,sizeof(q)); int k=bfs(i); if(num<k) num=k; } cout<<num<<endl; } return 0; }