参考文章:
- [CS231n课程笔记翻译:线性分类笔记(上)](https://zhuanlan.zhihu.com/p/20918580)
- [CS231n课程笔记翻译:线性分类笔记(下)](https://zhuanlan.zhihu.com/p/21102293)
本文概述:
0.基础:线性分类器(得分函数 + hingle loss(svm损失)、softmax分类器(交叉熵损失))
1.感知机与逻辑门
2.强大的空间非线性切分能力
3.网络表达力与过拟合问题
4.BP算法与SGD
0.基础:线性分类器
在传统的机器学习有监督学习中,核心是1.假设函数(得分函数) 2.损失函数(代价函数)。其中1. 假设函数是一个建模的过程,可以是LR(逻辑斯特回归),SVM,决策树等,将我们要解决的问题,公式化,抽象化,然后将我们经过特征工程处理好的数据输入到这个假设函数中,得到这个建模的 “得分”。因为我们是有监督学习,所以我们是知道正确的得分是多少的,因此2.损失函数上线了,将我们建模的得分输入到损失函数中,得到损失,再通过一些优化算法(如梯度下降)将我们的损失降低,进而优化我们的模型。
而在深度学习中,这里以图像分类为例,同样需要得分函数+损失函数:
0.1.得分函数



矩阵W的意义:
对于上图,简单看就是一个W*x + b = y的线性方程,那么深入研究一下,提出两个问题,1、为什么要用W * x 2、W是什么(它的行和列有什么意义)?
首先我们要说的是矩阵乘法,这里就是W的每一行,依次和x_i这一列相乘(再加上后面的偏置,得到一个得分列向量)。我们只看每一行与x这一列相乘,就相当于两个向量做点乘。
向量点乘(点积,向量内积)的物理意义是:向量之间的相似度。也称之cos相似度。点乘的几何(物理)意义是可以用来表征或计算两个向量之间的夹角,以及在b向量在a向量方向上的投影,有公式:
如果两个向量垂直,那么它们的点乘等于0,非常不相似,如果两个向量共线,夹角是0度,那么它们的点乘会很大,很相似。
回到W矩阵来看,W的每个行向量与x做点乘,其实就是为了找到了x非常相似的那个行向量,或者说学习(通过梯度下降和反向传播)这个行向量,也就是上图中红色的那一条(图中学的很糟糕,我们暂且不管)。
所以我们已经解释了第一问题,为什么要用W * x 。第二个问题,W有多少行,即代表了分有多少类别,比如上图中的猫,狗,船......。而W有多少列,即代表了x特征的维度,即x_i可能有什么特征,比如体重,身高,年龄......
总结:W*x是为了找与x相似度高的行向量,W的行的维度(个数)即类别的维度,列的维度(个数)即x特征的维度。
W往往称之为x的权重,我们要做的事情,就是不断改变w,找到最好的w,可以很好的将样本做分类(或回归)任务,这里的评价指标就是Loss Function。
解释:假设我们输入的图片维度是32x32x3,通过线性变形将其变成向量,维度是3072x1,通过与参数(权重)矩阵进行矩阵乘法,得到了分类向量(得分向量),该向量其中的每一个标量(即每个格子对应的数值)代表了每种分类的得分。上图猫的得分即-96.8,下面介绍如何评价这个模型的好坏,这个得分是否吻合真实的分类情况。
0.2.损失函数(代价函数)

损失函数 1: hingeloss/支持向量机损失

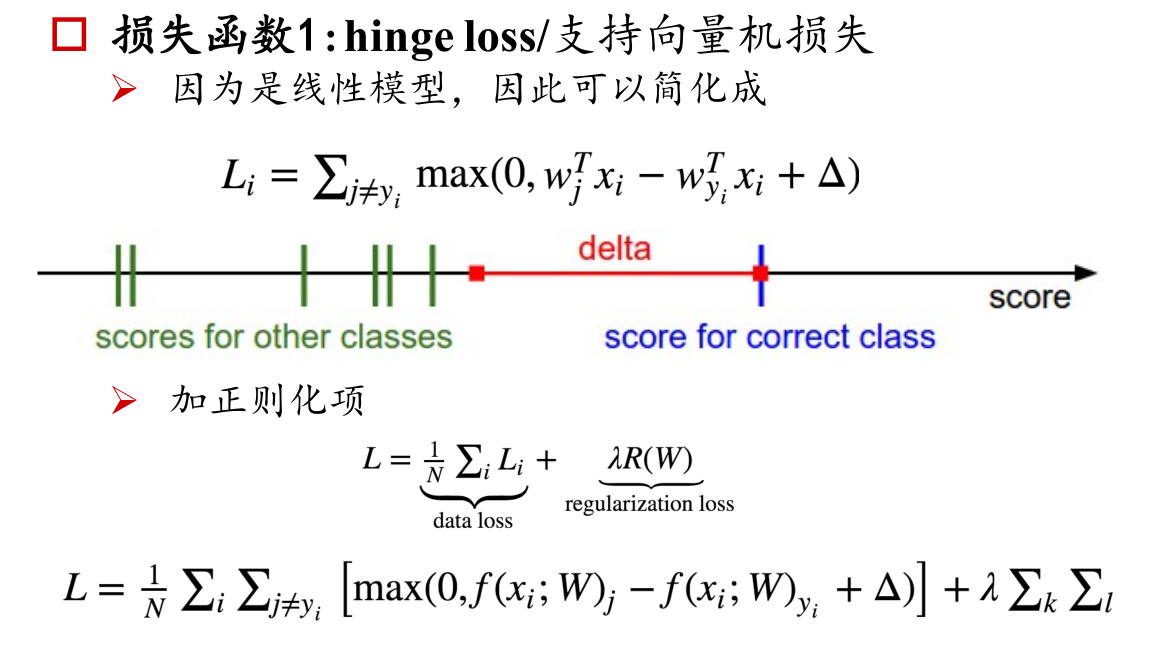
解释:hinge loss又称合页损失,通俗解释,SVM进行二分类的时候,在margin(两个支持向量中间的间隔区间)之外则是正确分类(hinge loss为0),如果样本点分类落在了margin里面,则认为是不正确的分类,hinge loss要惩罚这种分类的错误,损失不再为0,而是等于我们通过建模所假设的得分函数得到的分类值 - 正确的分类值 + delta。对delta的理解是对分类结果的容忍度,比如你考试考了100分,你的同学A只要考试低于90分,你都不会重视他,你可以容忍的是10分的差距,但是一旦他考了比如95分,你会发现他距离你的差距很小了,你开始重视起来他。放到SVM中,分类的决策边界“上”“下”各有一条支持向量构成的边界,这里姑且称之为A类边界、B类边界。样本X1原本属于A类,如果你位于A类边界下,那么正确分类,hinge loss为0,但如果你开始慢慢移动X1,让他位于margin中,那么hinge loss将不为0,越来越大。随着X1越来越接近B类边界,loss将越来越大,当你将X1分到了B类边界上面的时候,越往上分,loss会越来越大(如果你分类对了,只要X1位于A类边界下的时候,loss都是0,这是hinge loss不好的地方,我们后面会说)。
损失函数2 : 交叉熵损失(softmax分类器)


解释:上面两张图一起解释,对于第一张input猫咪的图片,最终得到的向量是cat、dog、ship的得分向量,我们希望把这个转变成一个概率向量,怎么做呢?
为了不改变各种种类(猫啊,狗啊,船啊等等)之间的相对大小,我们首先用exp(x)函数(它是一个单调函数),将原分类的得分值进行映射,
得到一系列∈(0, +∞)的值,然后进行归一化,即得到各个类别的概率(二分类到多分类就是这么来的,LR中的log损失,就是特殊的softmax损失)。然后类似LR中的lo损失,得到 ![]() 。
。

解释:比较这两个损失函数,hinge loss是一种心大的损失函数,它只要在安全界限以外,loss都为零,这样就很容易满足损失为0,模型迭代次数降低,优化可能不完善。
而要用交叉熵损失(交叉熵损失的步骤),首先要对真实值y_true做one-hot编码,然后对y_predict得分值通过softmax函数,将得分转换成概率(这中间有一个指数运算,计算量比较大)
, 最后进行交叉熵损失计算: L = -y_true * log(y_predict(概率向量))。
交叉熵损失的图像是-y_ture(=1) * log(p / 1),就是x = [ 分类正确的概率P / 所有类别加一起(就是1) ],将这个x放到 -log(x)中,希望它的值尽可能的小,这是一个无限接近于0的值。因为exp(x)的缘故(即使一些分类项的得分为0,exp(0)也等于1,而不是0),我们概率向量中,正确类的概率永远不可能是1,只可能无限接近1。这样带来的好处是,模型会不断迭代,不断优化,不满足仅仅是分类正确,而是分的好,分的妙,分的呱呱叫。
当然合页损失(hingle loss)不用将得分向量转换成概率向量,没有指数运算,减少了计算量。
1.感知机与逻辑门



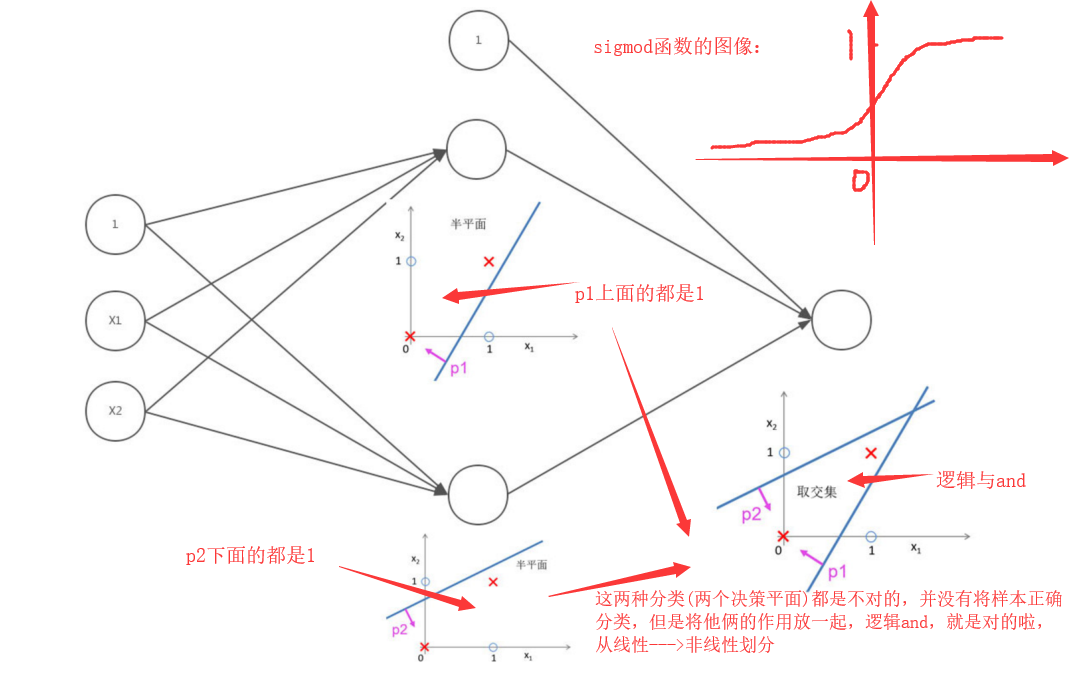
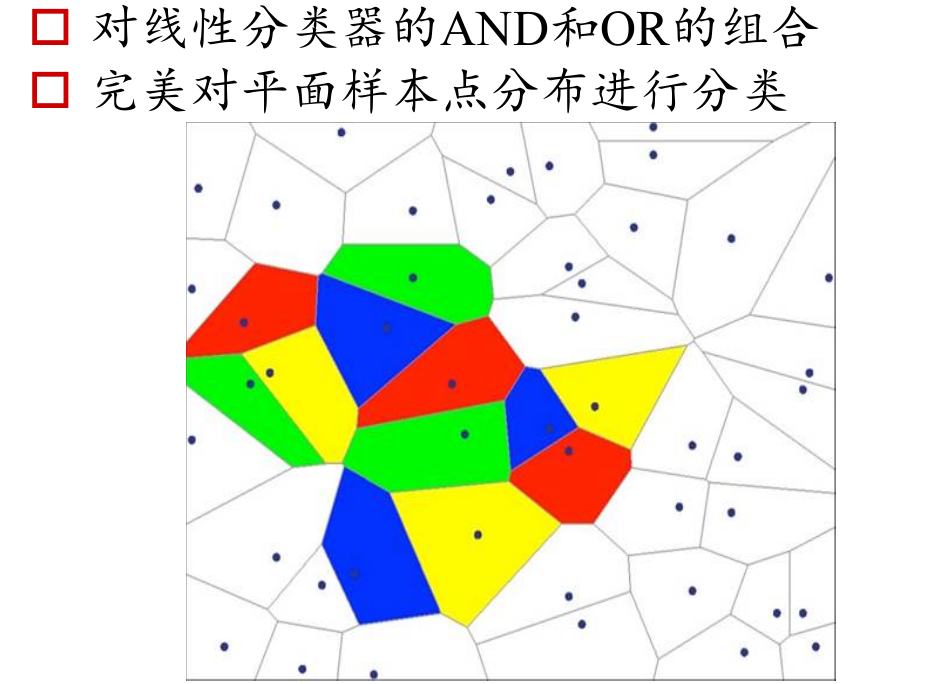
下面逻辑或同理,如果说逻辑与是将线性不可分的界面非线性可分,那么逻辑或就是将已经分对了的细化,变成更小的区域,可以分出来更小的一个一个的区域。


神经元的本质:之前我们介绍的线性分类器,y = w * x + b,可以理解成一条直线做分类。而神经元的本质,它只做一件事,非线性变换。
简单说,神经元就是一个做非线性变换的函数,而神经网络就是一个复合函数,里面有很多个做非线性变的神经元。
z = w * x + b,a = 激活函数(z)。z是一个线性分类器,a就是一个神经元。




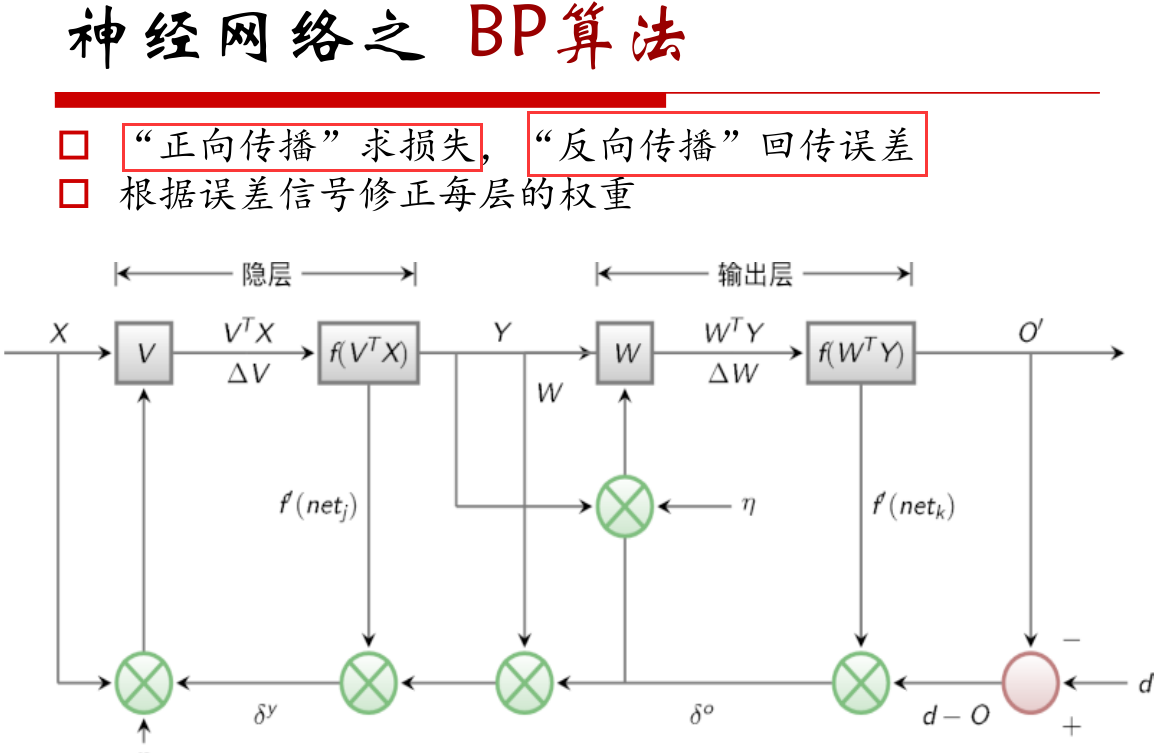


反向传播算法,其实就是一个链式求导的过程,它将误差(y_true与y_predict的误差)回传,通过计算每一层的梯度,进行优化,最终使得W和b不断优化。
从后往前计算,实际比如tf框架,在进行前向传播(求损失,当然不仅仅是求损失)的时候,就会保存每一层的梯度。
总而言之,前向传播求损失,反向传播回传误差。
