Random Walk
Time Limit: 5000/2000 MS (Java/Others) Memory Limit: 65535/65536 K (Java/Others)
Total Submission(s): 81 Accepted Submission(s): 35
Problem Description
Yuanfang is walking on a chain. The chain has n nodes numbered from 1 to n. Every second, he can move from node i to node j with probability:
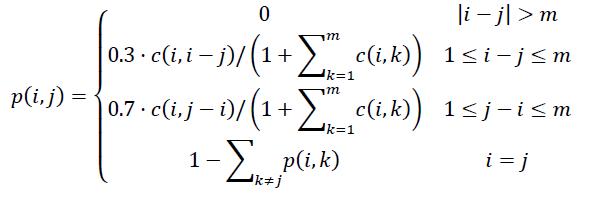
c(i,j) is an element in a given parameter matrix which is n×m. (1 <= c(i, j) <= 9)
Yuanfang wants to know the expectation time for him to walk from node 1 to node n.
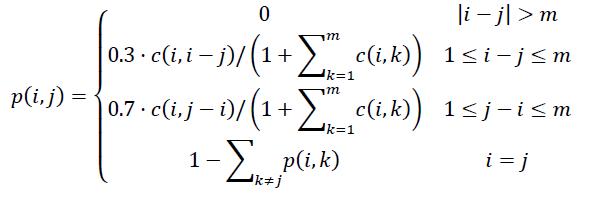
c(i,j) is an element in a given parameter matrix which is n×m. (1 <= c(i, j) <= 9)
Yuanfang wants to know the expectation time for him to walk from node 1 to node n.
Input
There are no more than 10 test cases.
In each case, there are two integers n (2 <= n <= 50000), m (1 <= m <= 5), in the first line, meaning that there are n nodes and the parameter matrix is n×m . There are m integers in each of the next n lines which describe the parameter matrix .
The input ends with 0 0.
In each case, there are two integers n (2 <= n <= 50000), m (1 <= m <= 5), in the first line, meaning that there are n nodes and the parameter matrix is n×m . There are m integers in each of the next n lines which describe the parameter matrix .
The input ends with 0 0.
Output
For each case, output the expectation time for Yuanfang to walk from node 1 to node n in one line. The answer should be rounded to 2 digits after decimal point.
Sample Input
3 1
1
1
1
5 2
1 2
2 1
3 2
2 3
1 3
0 0
Sample Output
6.94
8.75
Source
这题就是列出方程。
然后高斯消元解方程。
如果是一般的方程,高斯消元需要O(n*n)
但是这题的矩阵很特别
很快就可以消掉了。
用dp[i]表示i到n的期望。
dp[n]=0;
对于第i个方程,最多只有2*m+1个系数是不为0的。
1 /* ********************************************** 2 Author : kuangbin 3 Created Time: 2013/8/12 20:28:58 4 File Name : F:2013ACM练习比赛练习2013杭州邀请赛重现1004.cpp 5 *********************************************** */ 6 7 #include <stdio.h> 8 #include <string.h> 9 #include <iostream> 10 #include <algorithm> 11 #include <vector> 12 #include <queue> 13 #include <set> 14 #include <map> 15 #include <string> 16 #include <math.h> 17 #include <stdlib.h> 18 using namespace std; 19 const int MAXN = 50010; 20 double c[MAXN][10]; 21 double p[MAXN][20]; 22 double a[MAXN][10]; 23 double b[MAXN]; 24 double dp[MAXN]; 25 26 int main() 27 { 28 //freopen("in.txt","r",stdin); 29 //freopen("out.txt","w",stdout); 30 int n,m; 31 while( scanf("%d%d",&n,&m) == 2 ) 32 { 33 if(n == 0 && m == 0)break; 34 for(int i = 1;i <= n;i++) 35 for(int j = 1;j <= m;j++) 36 scanf("%lf",&c[i][j]); 37 for(int i = 1;i < n;i++) 38 { 39 double sum = 0; 40 for(int j = 1;j <= m;j++) 41 sum += c[i][j]; 42 double s = 0; 43 for(int j = 1;j <= m && i-j >= 1;j++) 44 { 45 p[i][m-j] = 0.3*c[i][j]/(1+sum); 46 s += p[i][m-j]; 47 } 48 for(int j = 1;j <= m && i+j <= n;j++) 49 { 50 p[i][m+j] = 0.7*c[i][j]/(1+sum); 51 s += p[i][m+j]; 52 } 53 p[i][m] = -s; 54 b[i] = -1; 55 } 56 for(int i = 1;i <= m+1 && i <= n;i++) 57 a[1][i] = p[1][m+i-1]; 58 for(int i = 2;i < n;i++) 59 { 60 int end = min(i+m,n); 61 int start = max(1,i-m); 62 63 for(int j = start;j < i;j++) 64 if(fabs(p[i][m+j-i]) > 1e-6) 65 { 66 double t = p[i][m+j-i]/a[j][1]; 67 for(int k = 1; k <= m+1 && j+k-1 <= n ;k++) 68 { 69 p[i][m+j-i+k-1] -= t*a[j][k]; 70 } 71 b[i] -= t*b[j]; 72 } 73 for(int j = 1;j <= end-i+1;j++) 74 a[i][j] = p[i][m+j-1]; 75 76 } 77 dp[n] = 0; 78 for(int i = n-1;i >= 1;i--) 79 { 80 for(int j = 2;j <= m+1 && i+j-1 <= n;j++) 81 b[i] -= dp[i+j-1] * a[i][j]; 82 dp[i] = b[i]/a[i][1]; 83 } 84 printf("%.2f ",dp[1]); 85 } 86 return 0; 87 }