《DSP using MATLAB》Problem5.33

        代码：

%% ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
%%            Output Info about this m-file
fprintf('
***********************************************************
');
fprintf('        <DSP using MATLAB> Problem 5.33 

');

banner();
%% ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

% -------------------------------------------------------------
%   x3(n) --- N-point circular convolution of x1(n) an x2(n)  
%   x4(n) ---          Linear convolution     
%   e(n)  ---       error sequence                            
% -------------------------------------------------------------

N = 8;
n1 = [0:3];
x1 = [2, 1, 1, 2];
N1 = length(x1);

n2 = [0:3];
x2 = [1, -1, -1, 1];
N2 = length(x2);


% --------------------------------------------
%        1st way ---- time domain
% --------------------------------------------
N
y1 = circonvt(x1, x2, N)
ny1 = [0:N-1];


% --------------------------------------------
%   2nd way ----  DFT method
% --------------------------------------------

y2 = circonvf(x1, x2, N);
ny2 = [0:N-1];


% --------------------------------------------
%   3rd way --- circulant matrix
% --------------------------------------------

y3 = circonvt_v3(x1, x2, N);
ny3 = [0:N-1];

% ---------------------------------------
%     Linear convolution
% ---------------------------------------

[y4, ny4] = conv_m(x1, n1, x2, n2);

%e1 = y1 - y4(1:N);



figure('NumberTitle', 'off', 'Name', 'P5.33 x1(n) and x2(n) N=4')
set(gcf,'Color','white'); 
subplot(2,1,1); stem(n1, x1); 
xlabel('n'); ylabel('x1(n)');
title('x1(n)');  grid on;
subplot(2,1,2); stem(n2, x2);  
%axis([-N/2, N/2, -0.5, 50.5]);
xlabel('n'); ylabel('x2(n)');
title('x2(n)');  grid on;


figure('NumberTitle', 'off', 'Name', 'P5.33 Cir-Conv(N=8) and Linear-Conv')
set(gcf,'Color','white'); 
subplot(2,2,1); stem(ny1, y1); 
xlabel('n'); ylabel('y1(n)');
title('Cir-Conv (Time domain), y1(n)');  grid on;
subplot(2,2,2); stem(ny2, y2);  
%axis([0, N, 0, 1]);
xlabel('n'); ylabel('y2(n)');
title('Cir-Conv (DFT method), y2(n)');  grid on;
subplot(2,2,3); stem(ny3, y3);  
%axis([-N/2, N/2, -0.5, 50.5]);
xlabel('n'); ylabel('y3(n)');
title('Cir-Conv (circulant matrix), y3(n)');  grid on;
subplot(2,2,4); stem(ny4, y4);  
%axis([-N/2, N/2, -0.5, 50.5]);
xlabel('n'); ylabel('y4(n)');
title('Linear-Conv, y4(n)');  grid on;

　　运行结果：

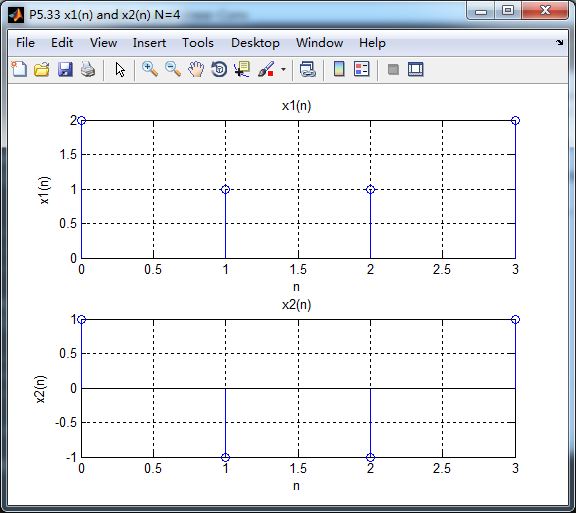
        y1--圆周卷积，N=4；y4---线性卷积，长度为7

        由下图可知，当N=7时，序列的圆周卷积和线性卷积结果相同。

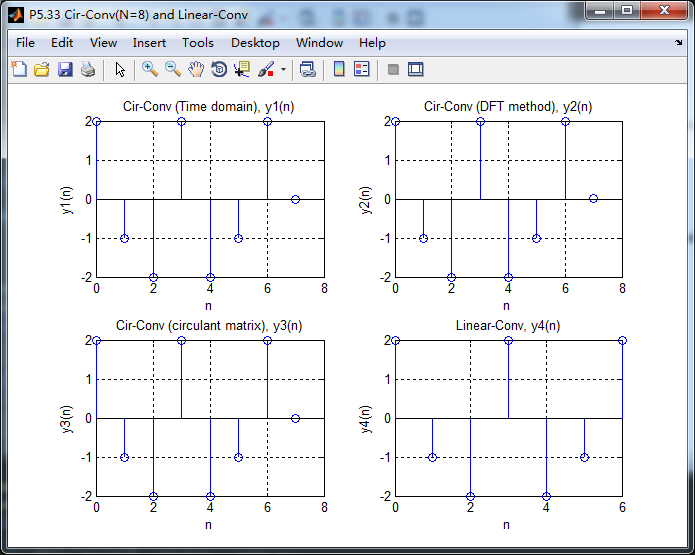
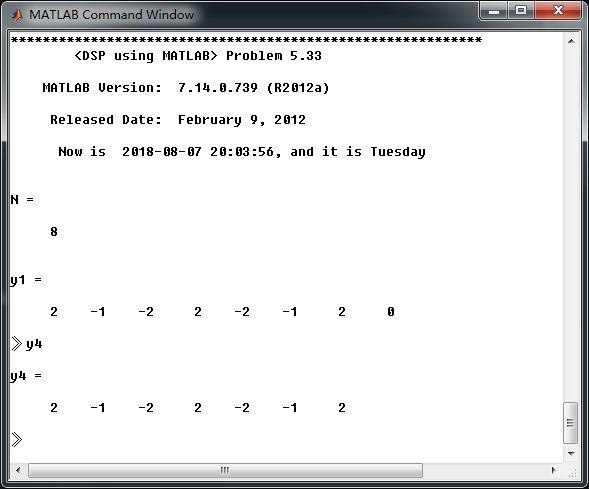
         结论：两序列x1长N1，x2长N2，当N至少取N1+N2-1做圆周卷积，结果和线性卷积相同。