Everything Has Changed
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 292 Accepted Submission(s): 155
Special Judge
Problem Description
Edward is a worker for Aluminum Cyclic Machinery. His work is operating mechanical arms to cut out designed models. Here is a brief introduction of his work.
Assume the operating plane as a two-dimensional coordinate system. At first, there is a disc with center coordinates (0,0) and radius R. Then, m mechanical arms will cut and erase everything within its area of influence simultaneously, the i-th area of which is a circle with center coordinates (xi,yi) and radius ri (i=1,2,⋯,m). In order to obtain considerable models, it is guaranteed that every two cutting areas have no intersection and no cutting area contains the whole disc.
Your task is to determine the perimeter of the remaining area of the disc excluding internal perimeter.
Here is an illustration of the sample, in which the red curve is counted but the green curve is not.
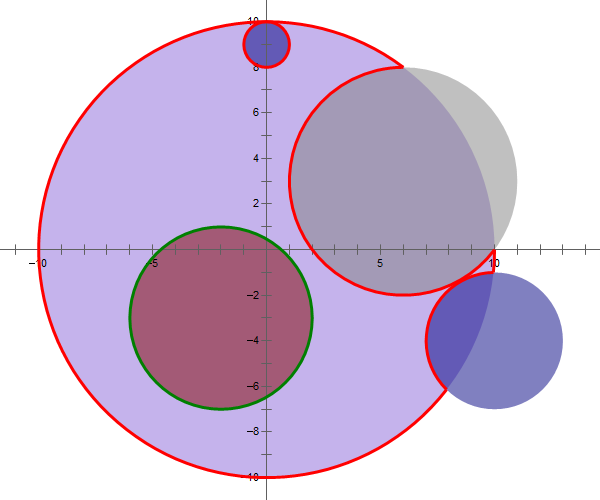
Assume the operating plane as a two-dimensional coordinate system. At first, there is a disc with center coordinates (0,0) and radius R. Then, m mechanical arms will cut and erase everything within its area of influence simultaneously, the i-th area of which is a circle with center coordinates (xi,yi) and radius ri (i=1,2,⋯,m). In order to obtain considerable models, it is guaranteed that every two cutting areas have no intersection and no cutting area contains the whole disc.
Your task is to determine the perimeter of the remaining area of the disc excluding internal perimeter.
Here is an illustration of the sample, in which the red curve is counted but the green curve is not.

Input
The first line contains one integer T, indicating the number of test cases.
The following lines describe all the test cases. For each test case:
The first line contains two integers m and R.
The i-th line of the following m lines contains three integers xi,yi and ri, indicating a cutting area.
1≤T≤1000, 1≤m≤100, −1000≤xi,yi≤1000, 1≤R,ri≤1000 (i=1,2,⋯,m).
The following lines describe all the test cases. For each test case:
The first line contains two integers m and R.
The i-th line of the following m lines contains three integers xi,yi and ri, indicating a cutting area.
1≤T≤1000, 1≤m≤100, −1000≤xi,yi≤1000, 1≤R,ri≤1000 (i=1,2,⋯,m).
Output
For each test case, print the perimeter of the remaining area in one line. Your answer is considered correct if its absolute or relative error does not exceed 10−6.
Formally, let your answer be a and the jury's answer be b. Your answer is considered correct if |a−b|max(1,|b|)≤10−6.
Formally, let your answer be a and the jury's answer be b. Your answer is considered correct if |a−b|max(1,|b|)≤10−6.
Sample Input
1
4 10
6 3 5
10 -4 3
-2 -4 4
0 9 1
Sample Output
81.62198908430238475376
Source
题意:给你一个圆心位于原点,半径为R的大圆,然后对大圆进行m次操作,每次切去小圆和大圆相交的区域,求切去这些区域后大圆剩余的外部周长
分析:高中几何数学问题。比赛的时候我怎么不自己去想想就给队友做了,明明上午才做过一个类似的要用到余弦定理的题目,自己写B题也写了两个对小时才A出来,导致最后才一个小时才A出这道题。
两圆相交分情况考虑:
外切外离内含不会切割大圆不用考虑
内切完整切割了一部分大圆区域,同时小圆的周长会全部成为大圆的外部周长,所以直接加上小圆的周长
相交小圆占了大圆一部分区域,大圆会损失一部分弧长,同时会得到小圆的一部分弧长,我们可以通过计算圆心角求出这部分弧长,圆心角可以通过圆心距和两个圆半径求出(这三个距离构成了一个三角形,通过余弦定理求)
AC代码:
#include <map>
#include <set>
#include <stack>
#include <cmath>
#include <queue>
#include <cstdio>
#include <vector>
#include <string>
#include <bitset>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <algorithm>
#define ls (r<<1)
#define rs (r<<1|1)
#define debug(a) cout << #a << " " << a << endl
using namespace std;
typedef long long ll;
const ll maxn = 1e2+10;
const ll mod = 998244353;
const double pi = acos(-1.0);
const double eps = 1e-8;
int main() {
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
ll T;
cin >> T;
while( T -- ) {
ll m, R;
cin >> m >> R;
double ans = 2*pi*R;
for( ll i = 0, x, y, r; i < m; i ++ ) {
cin >> x >> y >> r;
double dis = sqrt(x*x+y*y);
if( dis >= r+R ) { //外切外离不考虑
continue;
} else if( dis > fabs(R-r) && dis < R+r ) { //相交
double deg1 = acos((dis*dis+R*R-r*r)/(2.0*dis*R));
double deg2 = acos((dis*dis+r*r-R*R)/(2.0*dis*r));
ans -= deg1*2*R;
ans += deg2*2*r;
} else if( dis == R-r ) { //内切
ans += 2*pi*r;
}
}
printf("%.20lf
",ans);
}
return 0;
}