选址问题
清华大学肖勇波梁湧老师翻译的Rardin教授的《运筹学》[1]已于今年年中出版,感谢机械工业出版社张有利老师的推荐和赠书,让我能看到如此完美的千页级宏篇译著。该书的翻译质量非常高,书中内容深入浅出,附有大量的应用案例(Application)和练习题库。尤其让人欣喜的是该著作能与计算实践密切结合,凡有计算机图案标记的练习都是与计算和软件应用相关的,彰显了运筹学的应用数学本质。有鉴于此,笔者计划对该书中的问题进行大量实践,争取达到双位数的规模。
选址问题
此问题是该书中的一个练习,见原书第二章,练习2-39。此问题是第二章练习中比较复杂的一个。
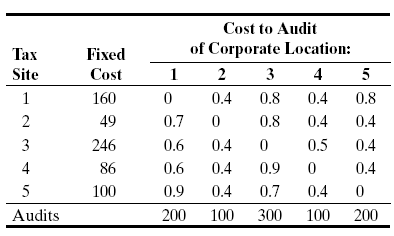
问题简述:有五个地点需要派员工作,拟在五个地点中选择若干个地点建立办公室,从办公室到工作地点的旅行根据远近不同有不同的耗费,在各地建立办公室的一次性花费也不同。已知各地的派员需求量,规划在何处建址以及各办公室到不同地点的派员数量,以使得总花费最小。数据如下:
+Leapms生成的模型摘录
对任何问题,+Leapms都建议直接用+Leapms建模语言直接写出模型,并进行模型调试。
我们的经验是,模型调试能够发现模型的不足、促进建模的完美性,甚至可以促进对问题的更加深入的了解。
当模型调试完毕,对模型的正确性有充分的信心后,+Leapms系统可生成模型摘录,包括数学概念模型(即使用标引符号表示的数学模型)和+Leapms源码供交流时使用。
使用x[i][j]表示从区域 i向区域j派员,显然如果有x[i][j]>0则在区域i必须建立办公室。使用0-1变量y[i]表示是否在区域i建立办公室。
以下是问题的+Leapms模型摘录(pdf屏幕截图):


+Leapms模型求解结果
+Leapms>load Current directory is "ROOT". ......... 02-01.leap 02-02.leap 02-03.leap 02-39.leap ......... please input the filename:02-39 ================================================================ 1: //2-39 To improve tax compliance the Texas 2: //Comptroller’s staff regularly audits at corporate 3: //home offices the records of out-of-state corporations 4: //doing business in Texas. Texas is considering 5: //the opening of a series of small offices near 6: //these corporate locations to reduce the travel 7: //costs now associated with such out-of-state audits. 8: //The following table shows the fixed cost (in 9: //thousands of dollars) of operating such offices at 10: //5 sites i, the number of audits required in each 11: //of 5 states j, and the travel cost (in thousands of 12: //dollars) per audit performed in each state from a 13: //base at any of the proposed office sites. 14: //======================================================= 15: //TaxSite|FixedCost|Costa 16: //======================================================= 17: // 1 2 3 4 5 18: // 1 160 0 0.4 0.8 0.4 0.8 19: // 2 49 0.7 0 0.8 0.4 0.4 20: // 3 246 0.6 0.4 0 0.5 0.4 21: // 4 86 0.6 0.4 0.9 0 0.4 22: // 5 100 0.9 0.4 0.7 0.4 0 23: //Audits 200 100 300 100 200 24: //======================================================= 25: //We seek a minimum total cost auditing plan. 26: 27: min sum{i=1,..m;j=1,..,n}c[i][j]a[j]x[i][j] + --> 28: sum{i=1,..m}f[i]y[i] 29: subject to 30: sum{i=1,..,m}x[i][j]= 1 | j=1,..,n 31: sum{j=1,..,n}x[i][j] <= M*y[i] |i=1,..,m 32: where 33: m,n are integers 34: M is a number 35: f[i] is a number|i=1,..,m 36: a[j] is a number|j=1,..,n 37: c[i][j] is a number|i=1,..,m;j=1,..,m 38: y[j] is a variable of binary|j=1,...,n 39: x[i][j] is a variable of nonnegative number --> 40: |i=1,..,m;j=1,..,n 41: data_relation 42: M=sum{j=1,..,n}a[j] 43: data 44: m=5 45: n=5 46: f={160 49 246 86 100} 47: c={ 48: 0 0.4 0.8 0.4 0.8 49: 0.7 0 0.8 0.4 0.4 50: 0.6 0.4 0 0.5 0.4 51: 0.6 0.4 0.9 0 0.4 52: 0.9 0.4 0.7 0.4 0 53: } 54: a={200 100 300 100 200} ================================================================ >>end of the file. Parsing model: 1D 2R 3V 4O 5C 6S 7End. .................................. number of variables=30 number of constraints=10 .................................. +Leapms>mip relexed_solution=0.712222; number_of_nodes_branched=0; memindex=(2,2) The Problem is solved to optimal as an MIP. 找到整数规划的最优解.非零变量值和最优目标值如下: ......... x2_2* =1 x2_4* =1 x3_1* =1 x3_3* =1 x3_5* =1 y2* =1 y3* =1 ......... Objective*=535 ......... +Leapms>
讨论
以上求解的变量结果与原著中给出的变量结果不一致,其原因是问题存在多解。
参考文献
[1] Rardin R. L 著,肖勇波、梁湧译. 运筹学. 北京:机械工业出版社,2018