D

D - Derivative

ZOJ - 3205

 

Calculating the derivative of a polynomial is an easy task. But what about calculating the derivative of , where is vector? Here we denote . To calculate the derivative of , you should know 5 rules:

1. , where is a vector here.
2. , where and means to take as constants for .
3. 
4. , where is a constant.
5. , where and is a constant.

Now your task is to calculate the first-derivative of for some given .

Input

The first line of the input contains an integer T (T <= 10), indicating the number of cases.

Each test case contains two blocks.
The first line of the first block contains two integers, n and m (0 < n, m <= 100), indicating the number of terms of the polynomial and the dimension of . The next n lines contain m + 1 integers each, C_i, p_i1, ..., p_im, indicating the coefficient and the exponent of x _j of the i-th term.
The first line of the second block contains one integer Q (0 < Q <= 100), indicating the number of queries for the given f(x). Each of the following Q lines contains m integers each, indicating the entry values of .

Note: All the values in the input are nonnegative integers not exceeding 100.

Output

For each query of each test case, output the resulting first-derivative vector in one line, with entries separated by one space and no extra space at the end of the line. For the result may be very big, you are only asked to output each element mod 1000000007.

Add a blank line between two consecutive test cases. There must be no extra blank line at the end of output.

Sample Input

2
3 2
1 2 0
3 0 2
7 0 0
2
1 4
2 3
2 2
1 1 1
9 1 0
2
1 4
2 3

Sample Output

2 24
4 18

13 1
12 2

Hint

The first-derivative of the first case is .
The first-derivative of the second case is .

数学题，将f(x)对x求导，得出方程

然后暴力求得

注意不要过多用模除操作，会超时啊。。。。。。

 

推导的方程：

 

代码如下：

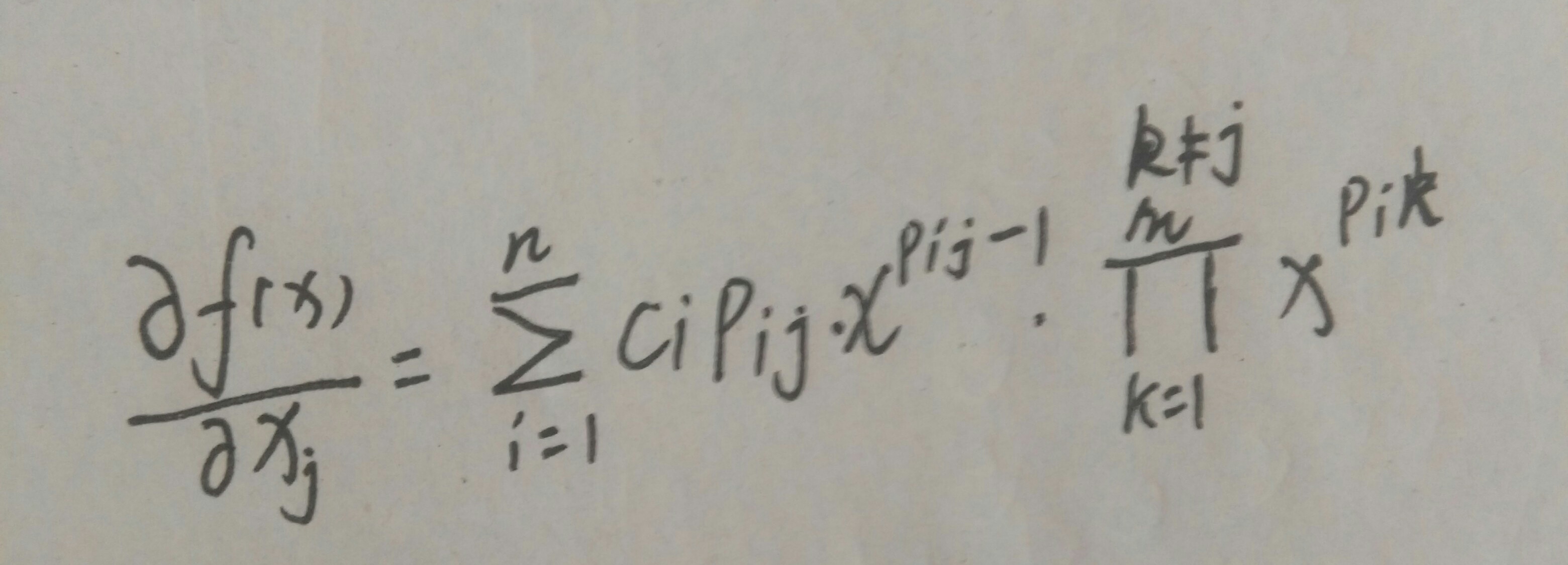
#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std;
const int N=103;
const int mod=1000000007;
typedef long long ll;
ll Pow[N][N];
void POW_init() //幂打表
{
    for(int i=0;i<N;i++){
            Pow[0][i] = 0;
            Pow[i][0] = 1;
    }
    for(int i=1;i<N;i++){
        long long t=1;
        for(int j=1;j<N;j++){
            t*=i;
            if(t>=1000000007) t%=1000000007;
            Pow[i][j]=t;
        }
    }
}
int main()
{
    POW_init();
    int t,n,m,q;
    ll p[N][N],c[N],x[N];
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d",&n,&m);
        for(int i=1;i<=n;i++)
        {
            scanf("%lld",&c[i]);
            for(int j=1;j<=m;j++)
                scanf("%lld",&p[i][j]);
        }
        scanf("%d",&q);
        while(q--)
        {
            for(int i=1;i<=m;i++)
                scanf("%lld",&x[i]);
            for(int i=1;i<=m;i++)
            {
                ll ans=0;
                for(int j=1;j<=n;j++)
                {
                    ll ant=1;
                    if(!p[j][i])   continue;
                    ant=(ant*c[j])%mod;
                    ant=(ant*p[j][i])%mod;
                    for(int k=1;k<=m;k++)
                    {
                        if(k==i)
                            ant=(ant*Pow[x[i]][p[j][i]-1])%mod;
                        else
                            ant=(ant*Pow[x[k]][p[j][k]])%mod;
                    }
                    ans=(ans+ant)%mod;
                }
                printf("%lld%c",ans,i==m?'
':' ');
            }
        }
        if(t)
            printf("
");
    }
    return 0;
}