什么是递归?
递归,就说函数在运行的过程中调用自己。
代码如下:
def recursion(n): print(n) recursion(n+1) recursion(1)
出现的效果,就是这个函数在不断的调用自己,每次调用n+1相当于循环。
结果如下:

可是为何执行了900多次就出错了?还说超过了最大递归深度限制,为什么要限制?
通俗讲,每个函数在调用自己的时候,还未退出,占内存,多了会导致内存崩溃。
本质上讲,在计算机中,函数调用是通过栈这种数据结构实现的,每当进入一个函数调用,栈就会加一层栈帧,每当函数返回,栈就会减一层栈帧。由于栈的大小不是无限的,所以,递归调用的次数过多,会导致栈溢出。
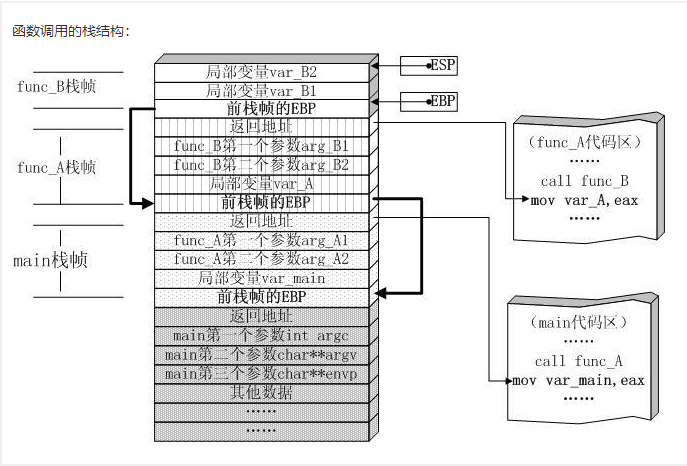
递归的特点
通过现象看本质,下面是用递归写的程序,让10不断除以2,直到0为止。
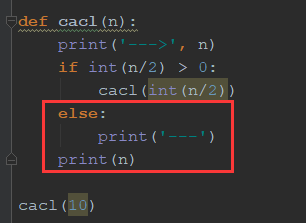
def cacl(n): print('--->', n) if int(n/2) > 0: cacl(int(n/2)) else: print('---') print(n) cacl(10)
运行结果:
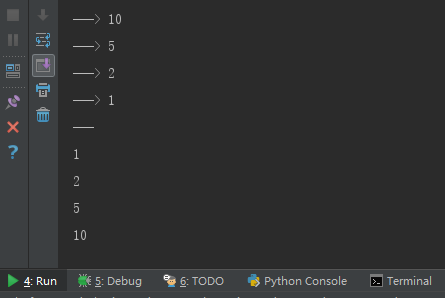
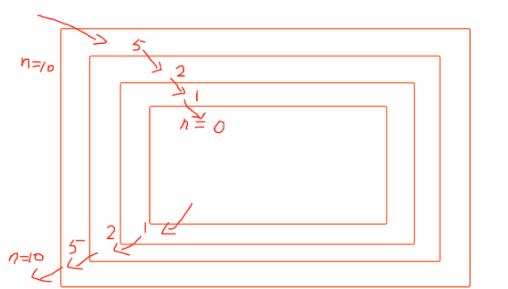
为何结果先打印10、5、2、1,然后又打印了1、2、5、10呢? 打印10、5、2、1可以理解,因为函数在一层一层的调用自己,但1、2、5、10是什么逻辑呢?因为当前函数在执行过程中又调用了自己一次,当前这次函数还没结束,程序就又进入了第2层函数调用,第2层还没结束就又进入了第3层,直到n/2>0不成立时才停止,此时问你,程序现在结束了吗?no,no,现在递归已经走到最里层,最里层的函数不需要继续递归了,会执行下方的else 判断。
打印的时1,然后最里层的函数就结束了。结束后会返回到之前调用它的位置,即上一层,上一层打印的时2,再就是5、10,即最外层函数,然后结束。
总结:
递归就是一层一层进去,还要一层一层出来。
最后的总结:
1. 必须有一个明确的结束条件,要不就会变成死循环,最后系统down。
2. 每次进入更深一层递归时,问题规模相比上次递归都应有所减少
3. 递归执行效率不高,递归层次过多会导致栈溢出
递归有什么用?
求阶乘
任何大于1的自然数n阶乘表示方法:
n! = 1*2*3*4*....*n
n! = n *(n-1)!
用递归代码来实现:
def fun(n): if n == 0: return 1 return n * fun(n -1) d = fun(0) print('*******',d)
二分查找
我们首先引入这样一个问题:如果规定某一科目成绩分数范围:[0,100],现在小明知道自己的成绩,他让你猜他的成绩,如果猜的高了或者低了都会告诉你,用最少的次数猜出他的成绩,你会如何设定方案?(排除运气成分和你对小明平时成绩的了解程度)
①最笨的方法当然就是从0开始猜,一直猜到100分,考虑这样来猜的最少次数:1(运气嘎嘎好),100(运气嘎嘎背);
②其实在我们根本不知道对方水平的条件下,我们每一次的猜测都想尽量将不需要猜的部分去除掉,而又对小明不了解,不知道其水平到底如何,那么我们考虑将分数均分
将分数区间一分为2,将第一次猜的分数将是50,当回答低了,将分数区间从【0,100】确定到【51,100】;
当回答高了,将分数区间从【0,100】确定到【0,50】.这样一下子就减少了多余的50次猜想(从0数到49)(或者是从51到100)。
③那么我们假设当猜完50分之后答案是低了,那么我们需要在【51,100】分的区间内继续猜小明的分数,同理,我们继续折半,第二次我们将猜75分,当回答是低了的时候,我们将其分数区域从【51,100】确定到【76,100】;当回答高了的时候,我们将分数区域确定到【51,74】。这样一下子就减少了多余的猜想(从51数到74)(或者是从76到100)。
④就此继续下去,直到回复是正确为止,这样考虑显然是最优的
代码如下:
data_set = list(range(101)) def b_search(n,low,high,d): mid = int((low+high)/2) if low == high: print('not found') return if d[mid] > n: print('to left :', low,high ,d[mid]) b_search(n, low, mid, d) elif d[mid] < n: print('to right :', low, high, d[mid]) b_search(n, mid+1, high, d) else: print('find it ', d[mid]) b_search(88,0,len(data_set),data_set)
运行结果:
