区间最小值*区间元素和最大（dp悬线法 ）

传送门

悬线法

题目大意：

对于一个长度为n的数列，找出一个子区间，
使子区间内的最小值与子区间元素和的乘积最大，
要求在满足舒适值最大的情况下最小化长度，
最小化长度的情况下最小化左端点序号。

 本题中我们可以考虑枚举最小值，将每个位置的数a[i]当作最小值，并考虑从i向左右扩展，找到满足  

的尽可能向左右扩展的区间  。这样本题就被转化成了悬线法模型这个题最主要的还是要求出l[i]和r[i]

l[i]和r[i]代表的是如果i是最小值的话向左和向右延申的最大下标

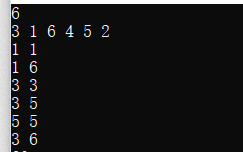
 例如

3：如果让3做最小值的话，下标最左是1，最右也是1

1：如果让1做最小值的话，下标最左可以达到1，最右可以达到6

，，，，，

#include <cstdio>
#include<algorithm>
#include<iostream>
#include <cstring>
using namespace std;
const int N = 100010;
int n, a[N], l[N], r[N];
long long sum[N];
long long ans;
int ansl, ansr;
bool fir = 1;
int main() {
  while (scanf("%d", &n) != EOF) {
    memset(a, -1, sizeof(a));
    if (!fir)
      printf("
");
    else
      fir = 0;
    ans = 0;
    ansl = ansr = 1;
    for (int i = 1; i <= n; i++) {
      scanf("%d", &a[i]);
      sum[i] = sum[i - 1] + a[i];
      l[i] = r[i] = i;
    }
    for (int i = 1; i <= n; i++)
      while (a[l[i] - 1] >= a[i]) l[i] = l[l[i] - 1];
    for (int i = n; i >= 1; i--)
      while (a[r[i] + 1] >= a[i]) r[i] = r[r[i] + 1];
    for (int i = 1; i <= n; i++) {
        cout<<l[i]<<" "<<r[i]<<endl; 
      long long x = a[i] * (sum[r[i]] - sum[l[i] - 1]);
      if (ans < x || (ans == x && ansr - ansl > r[i] - l[i]))
        ans = x, ansl = l[i], ansr = r[i];
    }
    printf("%lld
%d %d
", ans, ansl, ansr);
  }
  return 0;
}

#include <cstdio>
#include<algorithm>
#include<iostream>
#include <cstring>
using namespace std;
//悬线法 
/*
对于一个长度为n的数列，找出一个子区间，
使子区间内的最小值与子区间元素和的乘积最大，
要求在满足舒适值最大的情况下最小化长度，
最小化长度的情况下最小化左端点序号。
*/
typedef long long ll;
const int maxn = 100010;
int l[maxn],r[maxn],a[maxn];
ll sum[maxn];
ll ans;
bool fir = 1;
int ansl,ansr;
int main(){
    int n; 
    while (scanf("%d", &n) != EOF) {
        memset(a, -1, sizeof(a));
        if(!fir)
            printf("
");
        else
            fir = 0;
          ans=0;
          ansl=ansr=1;
          for(int i=1;i<=n;i++){
              scanf("%d",&a[i]);
              sum[i]=sum[i-1]+a[i];
              l[i]=i;
              r[i]=i;
        }
        for(int i=1;i<=n;i++){
            while(a[l[i]-1]>=a[i]) l[i]=l[l[i]-1];
        }
        for(int i=n;i>=1;i--){
            while(a[r[i]+1]>=a[i]) r[i]=r[r[i]+1]; 
        }
        for(int i=1;i<=n;i++){
            ll x=1ll*a[i]*(sum[r[i]]-sum[l[i]-1]);
            if(ans<x || (ans == x && ansr - ansl > r[i] - l[i])){
                ans=x;
                ansl=l[i];
                ansr=r[i];
            }
        }
        printf("%lld
",ans);
        printf("%d %d
",ansl,ansr);
    }
}