机器学习公开课备忘录(三)机器学习算法的应用与大数据集
对应机器学习公开课第六周和第10周
机器学习算法模型的选择与评价
1、对于一个data,可以将data划分为training set、test set和cross validation set三类(比例60%、20%、20%),其代价函数值分别为(J_{train}、J_{test}、J_{cv}),例如在构建新特征 (x) 的多项式时,可以假设不同的阶次 (d) 的 (x) 的多项式,利用training set得到各个多项式的具体参数,利用cross validation选择多项式模型中性能最好的一组,即确定最佳的 (d),而test set则用于评价最终模型的性能。
2、模型在泛化时中常见的两类问题是欠拟合与过拟合。前者代表数据有大的偏差,即平均值和真实值偏离;后者代表有大的方差,即平均值和真实值接近,但是波动幅度大。对于正则项,(lambda) 过大时引发了underfit(欠拟合)问题,反之则引发overfit(过拟合问题), (lambda) 的选择同样可以根据cross validation set来选择。绘制m和(J_{train}、J_{cv})的曲线,可以观察系统存在的问题:
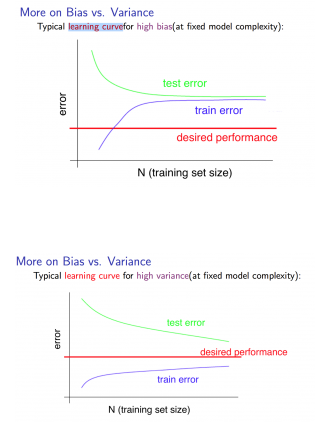
对于高偏差,最终测试集的误差和训练集误差随着样本m的提高非常接近,但是这误差值非常高,离我们期望值较远;而对于高偏差,测试集误差和训练集误差在m很大时仍然有一定差距,且随着m的增大而继续接近。这也说明,试图通过增大样本数量来改善模型性能的,只对高偏差的过拟合问题有效。
3、对于系统的过拟合和欠拟合问题,一些可以尝试的解决办法如下
| 解决方案 | 问题 |
|---|---|
| 更多data | high variance |
| 更少特征 | high variance |
| 增加额外特征 | high bias |
| 增加特征阶次 | high bias |
| 增大正则参数 | high bias |
| 减小正则参数 | high variance |
4、某些情况下,测试集的存在不能很好地评估系统性能,例如对于偏斜类问题(即分类问题中,某个类别特别少),因此还有一种评价方法:
| 预测真实 | 1 | 0 |
|---|---|---|
| 1 | true positive | false positive |
| 0 | false negative | true negative |
此时,有 $$查准率P = frac{TP}{TP+FP}$$ $$查全率R = frac{TP}{TP+FN}$$ $$F=2*frac{PR}{P+R}$$
大数据集的使用
梯度下降法的使用
1、在正式开始前,可以选用较小的数据集,绘制学习曲线,来大致寻找参数范围
2、批量梯度下降法需要读入所有数据才完成一次更新,在数据量过大时,速度很缓慢,为了提高速度,有两种方法:
a. 随机梯度下降法:每读入一个数据,就进行参数更新:$$ heta_j= heta_j-alpha(h_ heta(x{(i)})-y{(i)})x_j^{(i)} j=0,...,n $$ 直到将m个数据全部读入更新完毕,然后打乱数据集顺序,再重新读入一次,一般要重复1~10次;随机梯度下降法只能逼近最小值,但不能达到。若要绘制曲线,则可每读入一个数据,就计算该数据的代价,每扫描一定数量的数据,就计算平均cost,然后绘制一个点,最后得到曲线
b. 小批量梯度下降法:每读入b(1<b<m)个数据,就进行参数跟新:
say b=10,m=1000
repeat{
for i=1,11,21,...,991{
( heta_j= heta_j-alphafrac{1}{10}sumlimits_{k=i}^{i+9}(h_ heta(x^{(k)})-y^{(k)})x_j^{(k)} j=0,1,...,n)
}
}
在线学习机制
- 每读入一个数据,就进行更新,然后舍弃数据
- 能适应并反应用户偏好的变化
MAP REDUCE
- 分散计算——汇总,以此来加快求解速度
- 算法必须能表示成求和的形式