题目:度度熊有一张纸条和一把剪刀。
纸条上依次写着 N 个数字,数字只可能是 0 或者 1。
度度熊想在纸条上剪 K 刀(每一刀只能剪在数字和数字之间),这样就形成了 K+1 段。
他再把这 K+1 段按一定的顺序重新拼起来。
不同的剪和接的方案,可能会得到不同的结果。
度度熊好奇的是,前缀 1 的数量最多能是多少。
题目大意:……不用大意了原题目已经说的很清楚了。
分析:我们这一串数字中,前缀的1可以直接算在答案里,后缀的1可以花费一刀剪掉,中间的1需要花费两刀剪掉,如图:
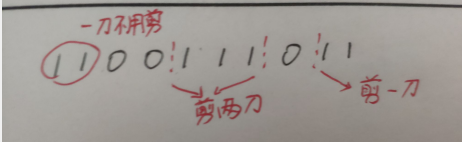
这样我们就可以把每一堆1所组成的组作为01背包中的一个单位,以其中1的数量为w,以k为容量做01背包。(我们把前缀的1的体积设为0,后缀1的体积设为1,中间的设为2)。然后做基础的01背包即可。
ps:直接贪心也可以解,给中间的1们按数量排序,然后从大到小加和,再比较一下是否加后缀也可以,但是需要考虑的细节太多(一晚上的头发你付的起吗),适合代码实现能力较强的同学尝试。
然后就
完了吗?
当然不是,你按照刚才我说的去打,一定会WA!!!!!!!!!
我们试想一组例子:
7 1
1011101
按照我们们刚才的想法,一定会得出2,实际上组样例的结果是3!!!
因为这组样例中出现了“中间比前缀更优的情况”。
我们一般会认为,前缀一块钱不花,白给的谁不要啊?这就犯了错误了,你在中间划一刀可能更优!
所以我们在比较时候需要让前缀1和其他1“公平竞争”,可以把它的体积设置为1,然后总容量k++,这样每次先遍历它的时候自然会把他加进去,而剩余容量也不变,如果遇到更好的,把它换走就好了。
我们还可以深入研究一下为什么要背包容量++。
事实上我们看1011101与0011101这两组数据,你砍两刀,结果都是4。
这是为什么呢?我们注意到,排位靠前的中缀1其实代价为1而不是2。
说起来也很好理解:你砍完一刀,中缀1的“1”就已经露出来了,你只需要把其他的往他上面粘就可以了。而前缀相当于一个默认“露头”的中缀1。
所以与其随机找到最大的中缀1让他的代价-1,还不如直接扩容背包,而前缀1其实是霸占了那个“优秀的”中缀1 的位置的。你若0代价选前缀,那么就不存在中缀砍1刀就出结果的过程了,所以我们为了不默认前缀1是那个被代价-1的,所以给他代价+1,这样在扩容背包,所有的1就都平等竞争了,不会存在谁“优秀”的问题了
思路清晰了,上代码!!!
#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> using namespace std; const int maxn=1e5+10; int a[maxn],v[maxn],w[maxn],f[maxn]; int n,k,cnt,Max; char s[maxn]; int main(){ while(scanf("%d%d",&n,&k)!=EOF){ memset(a,0,sizeof(a)); memset(f,0,sizeof(f)); memset(w,0,sizeof(w)); memset(v,0,sizeof(v)); cnt=0; //一些无聊的初始化 scanf("%s",s); for(int i=1;i<=n;i++){ a[i]=s[i-1]-'0'; }//用整形存,可不用。 for(int i=1;i<=n;i++){ if(a[i]==1){ cnt++;//含1的组数++ v[cnt]=2; while(a[i]==1&&i<n+1){ i++; w[cnt]++;//这个组1的数量 } } } if(a[1]==1){ v[1]=1; } if(a[n]==1){ v[cnt]=1; } k++; //第一块与最后一块的代价是1 if(k==1){ if(a[1]==1){ printf("%d ",w[1]); continue; }else{ printf("0 "); continue; } }//这里k==1,就是一刀都不让你切,直接等于前缀和 for(int i=1;i<=cnt;i++){ for(int j=k;j>=v[i];j--){ f[j]=max(f[j],f[j-v[i]]+w[i]); } }//01背包标准式 printf("%d ",max(f[k],Max)); } return 0; }