结构方程模型处理二阶混合型（反映性+形成性）构念的方法

1. 结构方程模型

1.1 测量模型与结构模型

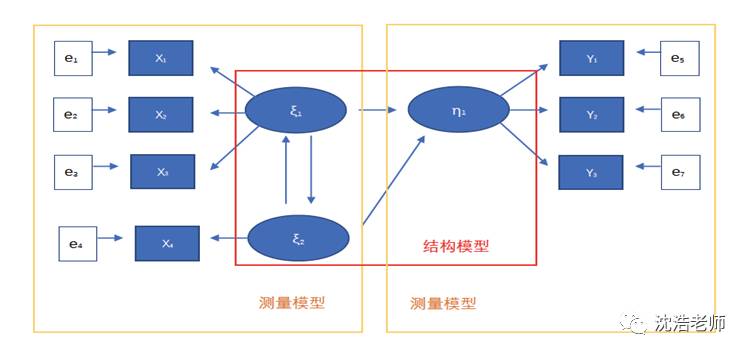
1.2 测量模型与结构模型方程

其中x为潜在自变量，y为潜在因变量

1.3 建模的限制

（1）模型必须是因果路径模型

（2）每一个潜变量至少应该和另一个潜变量相关

（3）每个潜变量至少需要一个观测变量

（4）每一个观察变量至少存在于一个潜变量上

（5）模型中只能存在一个结构模型

2. 形成性指标与反映性指标

2.1 反应型指标

在传统的SEM中，观测变量与潜变量之间为线性函数关系，潜变量的意义通过观测变量反映，潜变量的变化会导致观测标量的变化。（X1表示观测变量，e1表示误差,ξ1表示潜变量，λ1表示系数），传统的测量模型（反映性模型）可以用下式表达：

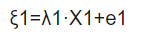
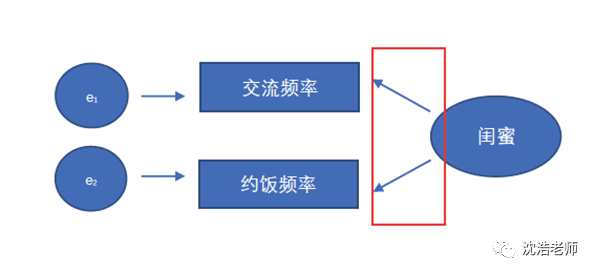
这类模型就被称为反映性测量模型(Reflective Measurement Model)，相应的观测变量即为反映性指标（Reflective Indicator）。举个例子：鉴定两个女生是否为闺蜜，就反映在她俩交流频率与约饭频率等方面。

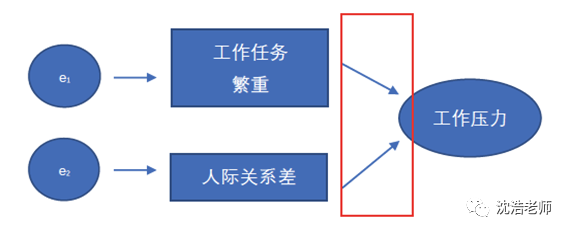
2.2 形成型指标

有些时候，潜变量的意义是由测量变量来决定的，这一类测量模型就称为形成性测量模型(Formative Measurement Model)，所对应的测量变量即为形成性指标（Formative Indicator）。举个例子：工作任务繁重，人际关系差等造成了工作压力。

ps:项目选择和量表评价必须考虑指标和潜变量间的方向性，应该采用形成性测量模型而不假思索的使用反映性测量模型将会严重影响量表的结构效度（Construct Vadility）和潜在构念的属性。

2.3 如何区分形成性模型与反映性模型

第一，指标是定义建构的特征还是建构的外在表现。如果指标所定义的特征联合起来解释建构的意义，那么形成性模型是合适的。如果指标是由构念决定的，那么应选择反映性模型。换句话说，可以通过判断潜在构念的变化引起指标的变化还是指标的变化引起潜在构念的变化来判断反映性模型还是形成性模型。

第二，指标是否可在概念上互换。如果是反映性指标，它们反映的是共同的主题，任何一个条目都是建构内容的实质性体现，所以可以互换。在心理测量学中，反映性指标其实就是一组行为样本，而形成性指标则不是。形成性指标之间并不必然含有共同成分，所以形成性指标捕捉了建构的独特部分，不能互换。

第三，指标是否彼此共变。反映性模型明确预示指标间彼此高相关，而形成性模型并没有这样的预测，它们之间即可以高相关，也可以低相关，甚至其他任何的相关形式。

最后，所有的指标是否具有相同的前因或/和后果。反映性指标反映相同的潜在构念所以它们具有相同的前因或/和后果。然而，形成性指标彼此不能相互替代，并且仅代表构念领域的特有部分，所以它们有着不同的前因和/或后果。

2.4 带形成性指标的例子

3. 指标重用方法相关说明（重要）

参考：A Critical Look at the Use of PLS-SEM in MIS Quarterly 附录B

3.1 指标重用

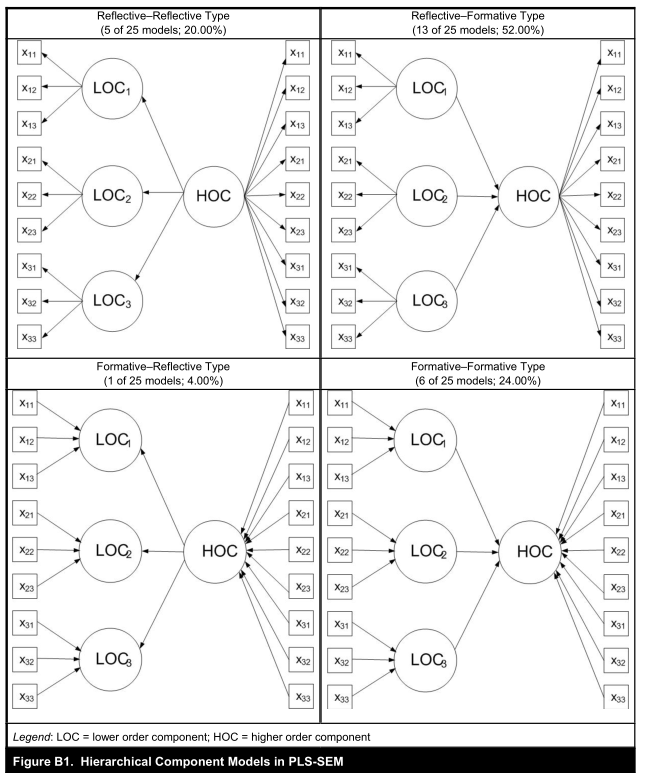
1. 高阶潜变量可使用低阶潜变量的所有指标作为其指标，当低阶潜具有相同的指标数量时这种方法效果最好，否则对低阶和高阶成分之间关系的解释必须考虑到较低阶组成部分中不等数量指标的偏差。该问题的潜在解决方案是计算和比较低阶分量指标和高阶分量之间的总效应。

2. 如图，高阶变量使用了低阶变量的指标

3.2 指标重用相关注意事项

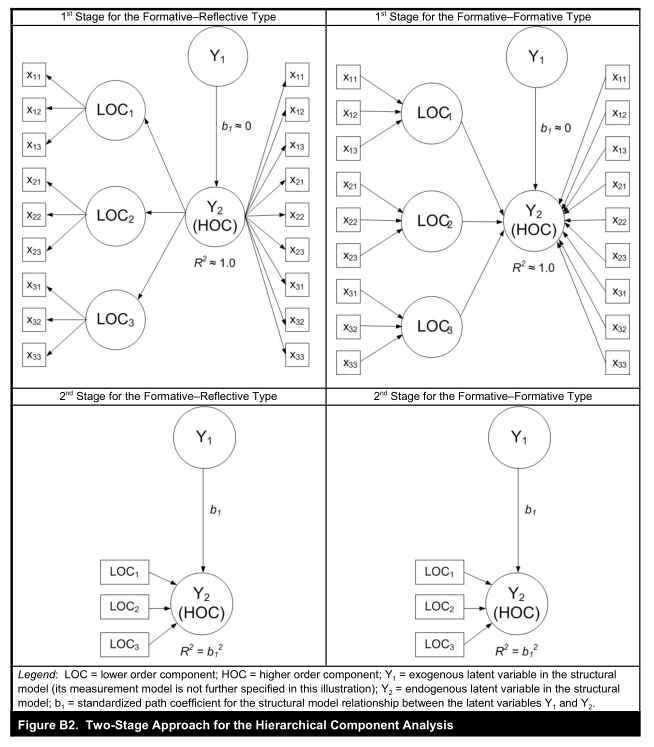
1. 如下图，当使用重复指标方法时，这些模型设置需要特别注意，因为高阶分量的几乎所有方差都由其低阶分量（LOC1-3）（R²=1.0;图B2）解释。 因此，从潜变量到内生高阶分量的路径关系总是近似为零且不显着(Y1不显著)。

2. 当遇到这种问题的时候，为了得到低阶潜变量到高阶潜变量的得分，可使用两阶段法，在第一阶段，人们使用重复指标方法来获得低阶分量的潜在变量分数，然后在第二阶段中，作为高阶分量的测量模型中的显性变量（图B2）。 因此，高阶分量以允许其他潜在变量作为前驱的方式嵌入在法则网中，以解释其一些方差，这可能导致显着的路径关系。
   （换种说法，第一阶段，利用indicators reuse approach，运行PLS，得到一阶因子的潜变量分数。第二步，将一阶因子的潜变量分数作为高阶变量的指标，重新运行PLS。这样，其他潜变量就可以解释此高阶变量的方差了，路径系数显著。
   ）

4. PLS算法的计算步骤

4.1 计算步骤示例

我们以下图的模型示例来说明PLS的计算步骤：

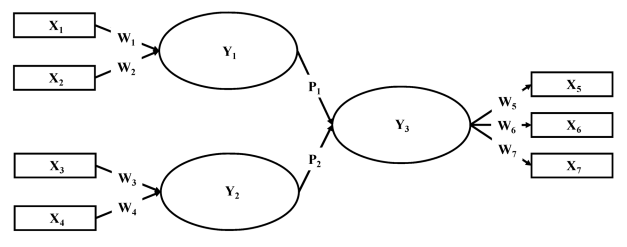
ps:图取自Hair, J. F., Ringle, C. M., & Sarstedt, M. 2011. PLS-SEM: Indeed a Silver Bullet. Journal of Marketing Theory and Practice, 18(2): 139-152.

PS：数据先标准化

第1步：反复的估计潜在变量的得分（latent construct scores，潛在概念分數），基本上就是去计算一个分数來代表潜在变量（construct），你可以简单的想象，一個潜在变量（construct）通常会有三个以上的低级指标（items）來衡量它，这代表了有一群数据反应出该潜在变量（construct），这样子的状况需要一个简单的数据来展现潜在变量（construct），简化指标（items）的数量（或者说是复杂度）但又可以展现指标的意义。所以PLS就用了以下的一套方法來估计一个分数给潜在变量（找对应的权重）。

• 1.1步：以上图的模型来说潜在变量（construct）Y1, Y2, Y3 的潜在变量分数（latent construct scores）。 基本上就是使用回归來估计每一个潜在变量（construct）的分数（latent construct scores）。

• 1.2步：用刚刚得到的分数來估计路径系数（path coefficients），以上图來说是要估计P1和P2。回归算权重。

• 1.3步：用1.1步的Y1, Y2, Y3 的潜在变量分数和1.2步的路径系数來调整潜在变量得分。即是因为之前算Y1, Y2, Y3 我们是直接用它们的低级指标来算的，而实际上他们还由其他的变量组成，比如Y3由Y1，Y2,x5,x6,x7组成，因此用他们重新估计之前没有考虑应该有路径的潜在变量得分。

• 1.4步： 上面的步骤已經能获得初步的潜在变量得分，接下來运用这些初步获得的得分重新去估计指标到潜变量的权重，基本上就是重新去计算W1~7

第2步：用最小二乘法來決定最後的指标到潜变量的权重（factor loading）和潜变量到潜变量的权重（path coefficients）估计值。简单点就不断的重复上面的操作直到这些权重的到一个稳定的值，收敛。

完成以上的步骤之后，就会得到一组W1~7, P1~2, 还有每一个潜变量的得分 。记住，这些数据都只会有一个，例如W1~7，就只是7個数据，展现出权重而已。但这样的结果并没办法让你知道你的模型好不好，也没有办法检验你的假说。

5. 模型评价

5.1 基本拟合标准

基本拟合标准是用来检验模型的误差以及误输入等问题。
主要包括：
（1）不能有负的测量误差；
（2）测量误差必须达到显著性水平；
（3）因子载荷必须介于0.5-0.95之间；
（4）不能有很大的标准误差。

5.2 模型内在结构拟合度

模型的内在结构拟合度是用来评价模型内估计参数的显著程度、各指标及潜在变量的信度。
主要包括：
（1）潜变量的组成信度（CR），0.7以上表明组成信度较好；
潜变量的CR值是其所有观测变量的信度的组合，该指标用来分析潜变量的各观测变量间的一致性
（2）平均提炼方差(AVE)，0.5以上为可以接受的水平。
AVE用于估计测量模型的聚合效度，反映了潜变量的各观测变量对该潜变量的平均差异解释力，即潜变量的各观测变量与测量误差相比在多大程度上捕捉到了该潜变量的变化。

5.3 整体模型拟合度

整体模型拟合度是用来评价模型与数据的拟合程度。
主要包括：
（1）绝对拟合度，用来确定模型可以预测协方差阵和相关矩阵的程度；
（2）简约拟合度，用来评价模型的简约程度；
（3）增值拟合度，理论模型与虚无模型的比较。
包括：
（1）χ2卡方拟合指数检验选定的模型协方差矩阵与观察数据协方差矩阵相匹配的假设。原假设是模型协方差阵等于样本协方差阵。如果模型拟合的好，卡方值应该不显著。在这种情况下，数据拟合不好的模型被拒绝。
（2）RMR 是残差均方根。RMR 是样本方差和协方差减去对应估计的方差和协方差的平方和，再取平均值的平方根。RMR应该小于0.08，RMR越小，拟合越好。
（3）RMSEA 是近似误差均方根 RMSEA应该小于0.06，越小越好。
GFI 是拟合优度指数，范围在0和1间，但理论上能产生没有意义的负数。按照约定，要接受模型，GFI 应该等于或大于0.90。
（4）PGFI 是简效拟合优度指数。它是简效比率(PRATIO，独立模式的自由度与内定模式的自由度的比率)乘以GFI。 PGFI 应该等于或大于0.90，越接近1越好。
（5）PNFI 是简效拟合优度指数，等于PRATIO乘以 NFI。 PNFI应该等于或大于0.90，越接近1越好。
（6）NFI 是规范拟合指数，变化范围在0和1间， 1 = 完全拟合。按照约定，NFI 小于0.90 表示需要重新设置模型。越接近1越好。
（7）TLI 是Tucker-Lewis 系数，也叫做Bentler-Bonett 非规范拟合指数 (NNFI)。TLI接近1表示拟合良好。
（8）CFI 是比较拟合指数，其值位于0和1之间。CFI 接近1表示拟合非常好，其值大于0.90表示模型可接受,越接近1越好。

6. 模型修改

参考文献

1. 统计建模 | PLS-SEM模型的理论与应用：企业声誉模型:http://www.sohu.com/a/200856374_715776
2. 结构方程模型与偏最小二乘法:https://wenku.baidu.com/view/4447dbd080eb6294dd886c5d.html?from=search
3. 形成性与反映性模型:http://blog.sina.com.cn/s/blog_7fb03f7d01013ivg.html
4. A Critical Look at the Use of PLS-SEM in MIS Quarterly
5. http://moodle.lips.tw/~tcasist/activities/2006/RALIS2006Autumn/RALIS2006Autumn09.pdf
6. PLS如何運作？:http://plsteaching.blogspot.com/2014/06/pls-sem-algorithm.html
7. 估計與檢驗你的結構模型:http://plsteaching.blogspot.com/2016/07/blog-post.html
8. 结构方程建模和分析步骤:https://www.coursera.org/lecture/jiegou-fangcheng-moxing/10-1-jie-gou-fang-cheng-jian-mo-he-fen-xi-bu-zou-wtaiR