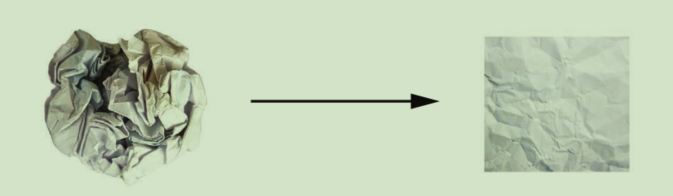
神经网络的工作内容就是张量计算(高维空间的几何变换),可以理解为将两张不同颜色的纸,揉成团以后的展开过程,使得两张纸再度可分。
数据的张量表示
人口统计数据集,其中包括每个人的年龄、邮编和收入。每个人可以表示为包含 3 个值的向量,而整个数据集包含 100 000 个人,因此可以存储在形状为 (100000, 3) 的 2D张量中。
一个以每秒 4 帧采样的 60 秒 YouTube 视频片段,视频尺寸为 144×256,这个视频共有 240 帧。4 个这样的视频片段组成的批量将保存在形状为 (4, 240, 144, 256, 3)的张量中。
逐元素运算
import numpy as np
z = x + y //逐元素的相加
z = np.maximum(z, 0.) //逐元素的 relu
张量广播
如果没有歧义的话,较小的张量会被广播(broadcast),以匹配较大张量的形状。广播包含以下两步。
(1) 向较小的张量添加轴(叫作广播轴),使其 ndim 与较大的张量相同。
(2) 将较小的张量沿着新轴重复,使其形状与较大的张量相同。
假设 X 的形状是 (32, 10) , y 的形状是 (10,) 。首先,我们给 y添加空的第一个轴,这样 y 的形状变为 (1, 10) 。
然后,我们将 y 沿着新轴重复 32 次,这样得到的张量 Y 的形状为 (32, 10)
获取不同维度的大小
>>> c = arange(20).reshape(5,4)
>>> c
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15],
[16, 17, 18, 19]])
c.shape[0]
5
Gives the number of rows
c.shape[1]
4
Gives number of columns
点积运算
def naive_vector_dot(x, y):
assert len(x.shape) == 1
assert len(y.shape) == 1
assert x.shape[0] == y.shape[0]
z = 0.
for i in range(x.shape[0]):
z += x[i] * y[i]
return z
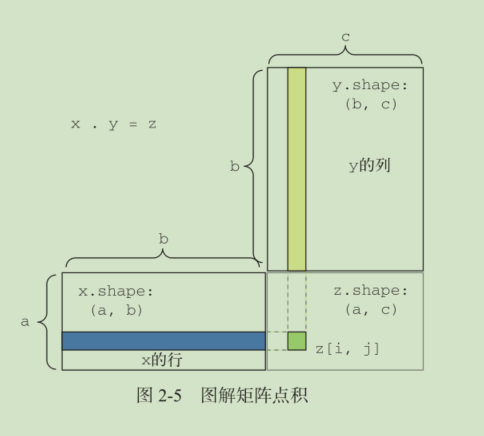
高维度计算
(a, b, c, d) . (d,) -> (a, b, c)
(a, b, c, d) . (d, e) -> (a, b, c, e)
变形
>>> x = np.array([[0., 1.],
[2., 3.],
[4., 5.]])
>>> print(x.shape)
(3, 2)
>>> x = x.reshape((6, 1))
>>> x
array([[ 0.],
[ 1.],
[ 2.],
[ 3.],
[ 4.],
[ 5.]])
>>> x = x.reshape((2, 3))
>>> x
array([[ 0., 1., 2.],
[ 3., 4., 5.]])
转置
>>> x = np.zeros((300, 20))
>>> x = np.transpose(x)
>>> print(x.shape)
(20, 300)
通常来说,仿射变换、旋转、缩放等基本的几何操作都可以表示为张量运算。举个例子,要将
一个二维向量旋转 theta角,可以通过与一个 2×2 矩阵做点积来实现,这个矩阵为 R = [u, v] ,其
中 u 和 v 都是平面向量: u = [cos(theta), sin(theta)] , v = [-sin(theta), cos(theta)]
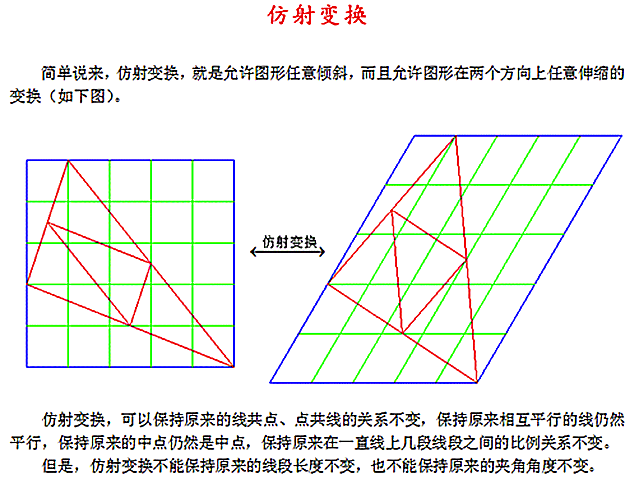
仿射变换是一种线性变换,如果想要神经网络学习更高维度的深层表示,需要加入relu等的激活函数。