首先f长得就很像能矩阵优化的,先构造转移矩阵(这里有一点神奇的地方,我看网上的blog和我构造的矩阵完全不一样还以为我的构造能力又丧失了,后来惊奇的发现我把那篇blog里的构造矩阵部分换成我的构造方式,交了一下完全没问题2333,并不知道为啥)
好久没写矩阵加速了,顺便说一下我的构造方法吧:
首先明确转移矩阵的目的,设m为构成f[i]的最小项f[i-m],也就是f[i]=f[i-m]+f[i-...]+f[i-...]+....,其中i-m是最小的。我们需要构造一个m大小的矩阵,使得{f[i-m],f[i-m+1].....f[i-1}乘上这个正方形矩阵变成{f[i-m+1],f[i-m+2]....f[i]}然后因为矩阵乘法是一行乘一列,所以每个右边的每个f[i]都对应了一行矩阵和左边的每项依次相乘。拿这道题的递推式,m=3为例:
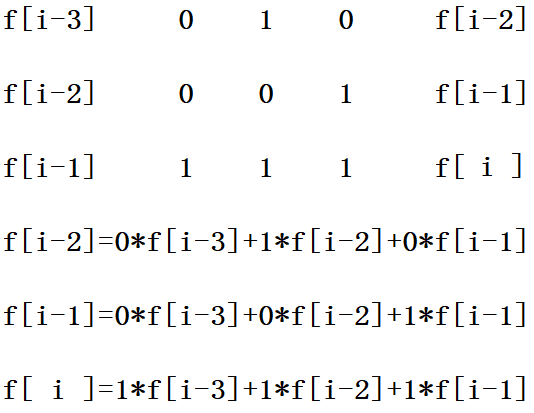
以上,我也不知道我在说什么。
然后这道题的精髓在于它使用f的矩阵进行g的dp。设f[i]为前i位的答案,因为矩阵乘法的结合律,我们可以记( g[i]=sum_{j=1}^{m}g[j]*c[j+1][i] )。然后考虑如何预处理出c,可以设c[i][j]为i这个数(1<=i<=9)的( j^{10} )次(假装高精)。
总之,一道好题。
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=505,mod=998244353;
int n,m;
char s[N];
struct qwe
{
int a[7][7];
void init()
{
memset(a,0,sizeof(a));
}
void pre()
{
memset(a,0,sizeof(a));
for(int i=1;i<=m;i++)
a[i][i]=1;
}
qwe operator * (const qwe &b) const
{
qwe c;
c.init();
for(int k=1;k<=m;k++)
for(int i=1;i<=m;i++)
for(int j=1;j<=m;j++)
c.a[i][j]=(c.a[i][j]+1ll*a[i][k]*b.a[k][j]%mod)%mod;
return c;
}
qwe operator + (const qwe &b) const
{
qwe c;
c.init();
for(int i=1;i<=m;i++)
for(int j=1;j<=m;j++)
c.a[i][j]=(b.a[i][j]+a[i][j])%mod;
return c;
}
}f[N],a,c[15][N];
qwe ksm(qwe a,int b)
{
qwe r;
r.pre();
while(b)
{
if(b&1)
r=r*a;
a=a*a;
b>>=1;
}
return r;
}
int main()
{
scanf("%s%d",s+1,&m);
n=strlen(s+1);
for(int i=1;i<=n;i++)
s[i]-='0';
for(int i=1;i<m;i++)
a.a[i][i+1]=1;
for(int i=1;i<=m;i++)
a.a[m][i]=1;
c[0][1].pre();
for(int i=1;i<=9;i++)
{
c[i][1]=c[i-1][1]*a;
for(int j=2;j<=n;j++)
c[i][j]=ksm(c[i][j-1],10);
}
f[0].a[1][m]=1;
for(int i=1;i<=n;i++)
{
qwe tmp=c[s[i]][1];
for(int j=i-1;j>=0;j--)
{
f[i]=f[i]+f[j]*tmp;
if(j&&s[j])
tmp=tmp*c[s[j]][i-j+1];
}
}
printf("%d
",f[n].a[1][m]);
return 0;
}