Sort

　　在这篇博客中将对我接下来进行的, 现有的排序算法的实现做一个汇总.

　　原地排序就是指不申请多余的空间来进行的排序，就是在原来的排序数据中比较和交换的排序。

1. 排序算法的性能评价

　　1). 评价排序算法好坏的标准: 执行时间和所需的辅助空间.

　　2). 排序算法的空间复杂度

　　　　若排序算法所需的辅助空间并不依赖于问题的规模n,即辅助空间是O(1),则称之为就地排序(In-Place Sort).

　　　　非就地排序一般要求的辅助空间为O(n).

　　3). 排序算法的时间复杂度

　　　　大多数排序算法的时间开销主要是关键字之间的比较和记录的移动. 有的排序算法其执行时间不仅依赖于问题的规模,

　　　　还取决于输入实例中数据的状态.

2. 排序算法汇总: 

　　为了避免本篇文章过于冗长,所以我对每一种排序算法都单独写了一篇文章.

　　1). 冒泡排序: http://www.cnblogs.com/lxw0109/p/bubble-sort.html

　　2). 选择排序: http://www.cnblogs.com/lxw0109/p/selection-sort.html

　　3). 插入排序: http://www.cnblogs.com/lxw0109/p/insertion-sort.html

　　4). 希尔排序: http://www.cnblogs.com/lxw0109/p/shell-sort.html

　　5). 堆排序: http://www.cnblogs.com/lxw0109/p/heap-sort.html

3. 各种排序算法的思想太重要了,对于解决很多问题都可以借鉴.

4. 基于比较的排序算法的时间复杂度下限为nlogn

证明: 要用基于比较的方法排序 A1,A2, A3, 其实就是找到一个两两比较序列，而这些序列都是下面这个二叉树中某一个从根到

叶子的路径

　　　　　　　　　　　　

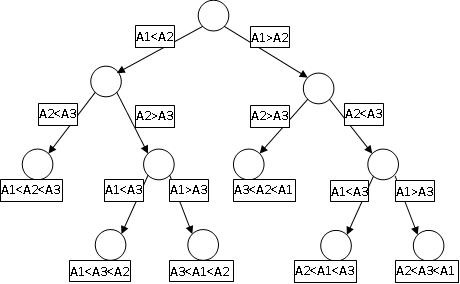
那么基于比较的排序的时间复杂度就是这棵树的深度H(N)。而且很容易知道叶子节点的个数就是N的排列 N！， 那么我们就有 

                          2^H(N) >= N! > N*(N-1)*.....*(N/2) > (N/2)^(N/2) 

                          H(N) > (N/2)lg(N/2) = O(nlgn)             得证

  

Reference:

基于比较的排序算法的时间复杂度下限: http://blog.sina.com.cn/s/blog_48b0843d0100hb0j.html