题目解析
我们发现译者在题面里加了一句非常有趣的话:
但是不保证端点所在的区间不重合
嘿嘿,(get)到了。
我们进行分类讨论,如果(r1<l2),那么事情就变得简单起来了:
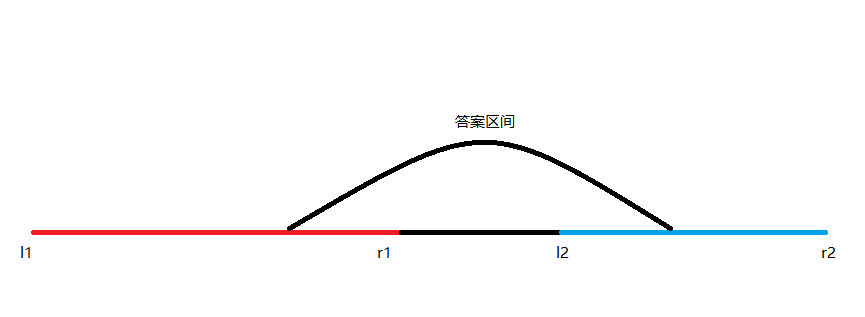
(ans=[l1,r1])的最大后缀+(sum[r1+1,l2-1])+([l2,r2])的最大前缀
然后那玩意儿用GSS1的方法维护就好了
而如果(r1>l2),也就是两个区间有交集,那么还会有更多种情况:
第一种:
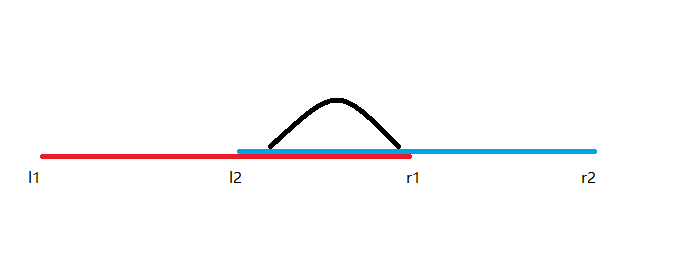
(ans=[l2,r1])的最大子段和
第二种:
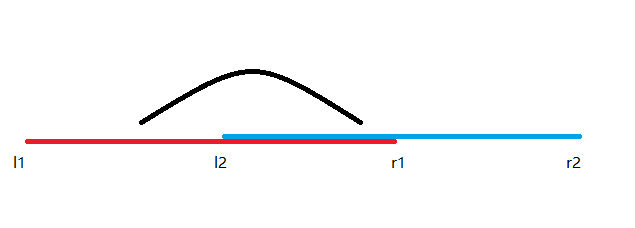
左端点在([l1,l2]),右端点在([l2,r2])
(ans=[l1,l2])最大后缀(+[l2,r2])最大前缀
第三种:
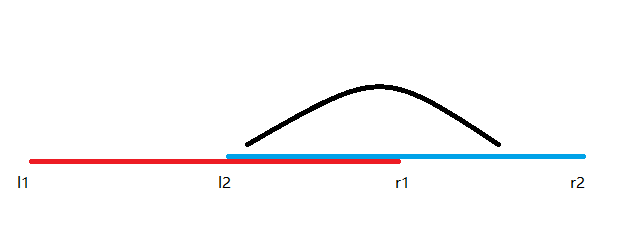
左端点在([l1,r1]),右端点在([r1,r2])
(ans=[l1,r1])最大后缀(+[r1,r2])最大前缀
以上三种情况都可以用GSS1的方法维护,三个方案取(max)即可。
但是,
这道题真没想的那么简单,
主要是它有很多边界上的细节容易出错,而且不好改。
首先,在(r1<l2)的情况里,有一个(sum[r1+1,l2-1]),这里可能在查询时出现(l>r)的情况,要特判一下。
其次,我们前面没有讨论(r1==l2)的情况。
我以为随便丢在哪种情况里都可以来着,但是如果丢在第一种情况,边界就会被算两次,所以最好丢到第二种情况去。
如果改成(ans=[l1,r1-1])的最大后缀+(sum[r1,l2])+([l2+1,r2])的最大前缀,那就意味着左右两个区间的端点必须是(r1-1)和(l2+1),但不一定啊,它可以不包括(r1-1)和(l2+1),所以这么写还要判断一下([l1,r1-1])的最大后缀和([l2+1,r2])的最大前缀是不是负数,如果是负数就不加(好麻烦
再然后,就是第二个大类里面的,我以为下面的边界可以归在左右随便哪个区间里就可以了,毕竟边界点总会在答案里。
但没有想到的是,这道题它不能随便,虽然边界点总会在答案里,但是不同的写法对边界点左右两边是否一定要在区间里产生影响(类似于刚才的那个讨论)。这么说可能有点抽象,我具体写在代码注释里了。
►Code View
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
#define LL long long
#define N 10005
#define DEL 100000
#define INF 0x3f3f3f3f
#define MOD 998244353
LL rd()
{
LL x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1; c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48); c=getchar();}
return f*x;
}
int n;
struct node{
int sum,mx,mxl,mxr;
}tree[N<<2];
void PushUp(int i)
{
tree[i].sum=tree[i<<1].sum+tree[i<<1|1].sum;
tree[i].mx=max(max(tree[i<<1].mx,tree[i<<1|1].mx),tree[i<<1].mxr+tree[i<<1|1].mxl);
tree[i].mxl=max(tree[i<<1].mxl,tree[i<<1].sum+tree[i<<1|1].mxl);
tree[i].mxr=max(tree[i<<1|1].mxr,tree[i<<1|1].sum+tree[i<<1].mxr);
}
void Build(int i,int l,int r)
{
if(l==r)
{
tree[i].sum=tree[i].mx=tree[i].mxl=tree[i].mxr=rd();
return ;
}
int mid=(l+r)>>1;
Build(i<<1,l,mid);
Build(i<<1|1,mid+1,r);
PushUp(i);
}
node Query(int i,int l,int r,int ql,int qr)
{
if(ql>qr)
{//边界+1-1之后可能会出现这种情况 需要特判
node res;
res.sum=res.mx=res.mxl=res.mxr=0;
return res;
}
if(ql<=l&&r<=qr) return tree[i];
int mid=(l+r)>>1;
if(qr<=mid) return Query(i<<1,l,mid,ql,qr);
else if(ql>mid) return Query(i<<1|1,mid+1,r,ql,qr);
else
{
node x=Query(i<<1,l,mid,ql,qr),y=Query(i<<1|1,mid+1,r,ql,qr),res;
res.sum=x.sum+y.sum;
res.mx=max(max(x.mx,y.mx),x.mxr+y.mxl);
res.mxl=max(x.mxl,x.sum+y.mxl);
res.mxr=max(y.mxr,y.sum+x.mxr);
return res;
}
}
int main()
{
int T=rd();
while(T--)
{
n=rd();
Build(1,1,n);
int Q=rd();
while(Q--)
{
int l1=rd(),r1=rd(),l2=rd(),r2=rd();
if(r1<l2)
{//这里不能取等 不然边界会被算2次
node x=Query(1,1,n,l1,r1),y=Query(1,1,n,l2,r2),z=Query(1,1,n,r1+1,l2-1)/*注意边界+1-1*/;
printf("%d
",x.mxr+z.sum+y.mxl);
}
else
{
int res=Query(1,1,n,l2,r1).mx;
node x=Query(1,1,n,l1,l2-1),y=Query(1,1,n,l2,r2);
//啊 这里之前写的 x=Query(1,1,n,l1,l2),y=Query(1,1,n,l2+1,r2) 就过不了
//那样写的话 右端点恰好在l2上的情况就无法被计算到
//而左端点恰好在l2上的情况可以在第一种和第三种情况中被计算
//同理 下面也必须写成r1和r1+1 否则左端点恰好在r1的情况就无法被计算到
res=max(res,x.mxr+y.mxl);
x=Query(1,1,n,l1,r1),y=Query(1,1,n,r1+1,r2);
res=max(res,x.mxr+y.mxl);
printf("%d
",res);
}
}
}
return 0;
}