看了Opengl的相关程序,发现有些东西还是特别迷茫,尤其是gluLookAt的函数做啥用的,而gluPerspective又有什么功能.
在网上查看到了这篇: 终于搞明白gluPerspective和gluLookAt的关系了(zz)
http://cowboy.1988.blog.163.com/blog/static/751057982010101574732212/
我感觉它里面没有说清楚这些函数到底是做什么用的,只是说了不同的参数有什么效果. 我相信它做法是对的,但我更希望获取why to do it? not just how to do it.
然后在网上又搜索到了: OpenGL入门学习[五]
http://apps.hi.baidu.com/share/detail/22508949
这篇比上面的稍微更加详细点,但没有系统的归纳,感觉有个断层在上面.
从而不得已,再把先前的书(计算机图形学--with opengl的描述)再翻了一遍前面部分.从而有了一个大概的思路.
也把我现在的困惑解开,我相信一些初学者也会从中得到启发(如果能够帮助您解惑,那就是我写这篇blog的最大回报了).
对于二维的图形开发,拿简单的图片显示来说,我们主要的目的:就是在一块显示buffer中,不停的把每个像素进行着色,然后就可以绘制出来了.为了速度,很多其他的加速方法,但原理基本上就是这样了. 很直观,也很简单. 就像我们在画布上进行着色,就可以了.
习惯了上面的二维的图形开发,我们来到三维世界,感觉一下子找不到北了. 怎样把颜色绘制上去了?怎样旋转/怎样平移呢?等等问题都一一来了.
如果这时候,你去网上搜的话,有很多网页都会提到只要调用某个函数就可了.(opengl里面有现成的函数)
我们先不跳入到具体的函数里面,而是把三维的图像绘制来整理一遍.
二维的图像显示,我们感觉是在画布上着色,而在三维的图像显示,就相当于用照相机照相了.尽管最后底片上冲印出来的照片是二维的,但这个过程中就不再象我们二维那么简单的去着色了,它里面有一个转换的过程.如果我们知道了这个转换过程,反过来来看相应的函数,就知道为什么是这样了.
坐标系的区分我们就不提了,很多书上都写过,也比较好理解.
一般来说,建模时采用建模坐标系,然后在绘制的时候,先把建模坐标系转换到世界坐标系.
opengl的坐标系, Z的正方向指向屏幕外的(属于右手坐标系),X的正方向指向右, Y的正方向指向上.
我们假设在前面某个点(0,10,-10) 放置了一个茶杯. 我们这样把这个茶杯显示在屏幕上呢? 如果是二维的开发,我们估计直接把茶杯的图片显示出来,而现在在三维上,我们是用相机来拍照,场景里面就不只是一个茶杯了,还有其他的东西,并且茶杯如何体现它的三维的成像,也是一个问题.
既然是拍照,我们就需要把相机的位置调整好,这一般来说就是一个视点(看的地方). 然后我们需要调整相机的朝向,这个也好理解.
剩下的问题是,我相机也选好位置了(0,10,0),方向也选好了(指向(0,0,-1)). 好,这时我们要考虑一个初学者容易想不清楚的问题,茶杯如何在观察屏幕显示出来呢?
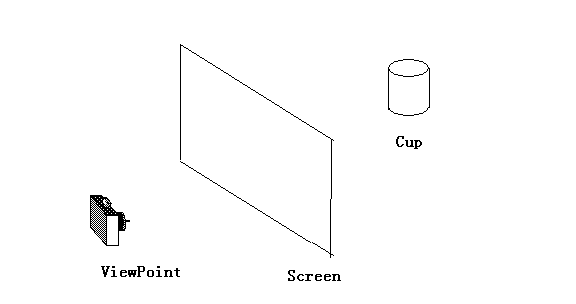
上面简单的绘制了一个示意图,为了把Cup绘制到Screen上,我们需要做下面的变换.
首先,我们建立一个观察坐标系,其原点在(ViewPoint)上,然后我们需要一个观察平面(也就是上面的Screen,注意这个和真正屏幕显示出来的有点差别,会有另外一个对应关系,不过也就是二维的变换,我们就不仔细区分). 现在我们就想把Cup的形状在观察平面上投影,注意是投影. 这个投影的结果也就是我们绘制的结果.
既然是投影,就和坐标有关联了,因此我们必须把Cup都统一转换到观察坐标系里面来,这个过程涉及到平移/旋转等操作.
当我们把Cup的坐标和模型都使用了观察坐标系表示之后, 就要开始真正的投影了.
投影从数学角度来说,是比较简单和直观的. 正交投影和透视投影是两种不同的投影.我在这边把它比如成光源.正交投影,就是有一排平行于观察平面的法线的方向的光源,它发出一组平行线,从而不管物体离观察平面的远近,大小都是一样的.
而透视投影,类似于有个点光源,它会发出一组相交于一点的光线,从而相同的大小,近的物体投影的大小大,而远一些的就小一点.
投影之后,就在观察界面有了显示,这就是我们最终的成像了. 观察平面从数学来说是无线大的,从我们实际使用角度,我们需要限制一个大小,这个大小也就决定了,我们那些区域可以显示,其他投影在别的区域就忽略).这就是很多书上说的裁剪窗口.
针对不同的投影,可以计算出每个点(x,y,z)在观察平面的投影的位置(Xview, Yview, Zview). 问题就来了,不同的点有可能映射到相同的位置,怎样来区分??? 我发现前人真的很聪明,他们把这些投影的位置,他们引入了投影转换的概念,使得先前物体的位置的z保持不变,而把(x,y)转换到(Xview,Yview).这样我们就发现,在前面的裁剪空间(人为的选定一个z轴的near和far的区域),这个区域中就保存了很多相同的点(Xview,Yview)只是z坐标不同. 然后我们根据远近的原则,就可以确定最终在观察平面上的点是由那个空间点来决定的. 一般来说,为了统一化,经过投影转换(也就是把x,y转换成最终的映射到观察平面的点(Xview,Yview)),我们就形成了一个统一的区域(这时就相当于正交投影了). 因为这时每个点的x,y坐标和最终映射到观察平面是一致的. 这时统一之后,为了更加快捷操作,可以进一步做规范化处理(使得每个坐标轴都在(-1,1)的范围),然后进行区域裁剪,可见面的绘制,光照等着色处理.这样就形成了最后的成像.
在正交投影时,就类似于我们在观察平面上每个点(Xview,Yview)可以找到所对应的物体(根据zBuffer来进行深度测试等).这样就能使得前面的物体可以挡住后面的物体. 最终就是通过投影变换,把不同的投影都转换成最终的正交投影,然后感觉z轴的不同进行深度测试,从而可以区分那些物体可以先画,那些物体被遮挡. 统一了就好办多了.:)
成像之后,我们在把成像的内容放到屏幕上去显示(这有点类似于照片底片的冲印). 我们观察平面的裁剪窗口的大小和屏幕的大小可以一致,也可以有差别. 但为了使得最终的效果基本一致,所以,一般设置成它们具有相同的 aspect(横纵比 w/h), 从而它们的转换关系就是等比例的放大或者缩小,而不会产生扭曲.
上面这个过程,也就是我们三维显示的过程.那怎样和opengl来关联呢?这就要调用opengl的相关函数了.
网上讲解这些函数的很多,但和我们上面理解的过程如何对应起来的很少,很少.
首先:我们需要把显示的物体转换到观察坐标系
如果物体有自己的建模坐标系,则需要把这个转换到世界坐标系,然后再转换到观察坐标系.
既然坐标系的转换,那我们首先要建立观察坐标系.
因此,我们首先要选取观察坐标系的(原点,z轴的,以及y轴的方向),通过z轴和y轴的方向,可以确定x轴的方向.
这个过程,opengl用
gluLookAt(GLdoble eyex,GLdouble eyey,GLdouble eyez,GLdouble centerx,GLdouble centery,GLdouble centerz,GLdouble upx,GLdouble upy,GLdouble upz);
函数来制定了, 它选取 eyex,eyey, eyez 做为原点(观察坐标系的坐标(用世界坐标系来表示的)),然后centerx, centery,centerz 指定了观察方向(z轴的反方向), upx,upy,upz 指定了y轴的正方向的近似方向(它不一定和z轴方向正交,但可以通过相关的运算,找到正交的Y轴的正方向,从而也可以找到x轴的正方向.主要就是通过向量的点乘和叉乘来计算的)).
指定了这些,从而也就建立了从世界坐标系到观察坐标系的转换的矩阵.opengl的把这个转换的矩阵保存在矩阵堆栈中,从而后面就自动的把其他的世界坐标系转换到观察坐标系里面). 坐标系的转换,也就是物体的描述转换到观察坐标系里面了.从而后面的投影,就统一在观察坐标系里面来计算.
这就是gluLookAt的函数的作用,它封装了世界坐标系到观察坐标系的转换. 它在:glMatrixMode(GL_MODELVIEW);
的模式下调用的.
我们这样来阐述了 gluLookAt的函数的原理和作用.现在应该清楚它是怎样来的,为什么来的吧? 说简单就是为了建立坐标系的转换,把所有的物体都用观察坐标系来描述. 而不是从函数的名称来看,感觉是让我们看某个地方,尽管它有点这方面的含义,但不直观.
OK,我们明白了gluLookAt的作用,调用之后,我们就把坐标系变换的矩阵放入了矩阵栈,后续对物体的位置描述,会通过此矩阵栈进行转换到我们的观察坐标系了.
从这点来说,还是很佩服opengl的设计者的思路,把变换矩阵进入了堆栈来保存,从而在绘制不同的物体时,不需要把它当成额外的参数带入.使得使用起来更加方便/直观. 不过初学者,有些时候就感觉找不到北了,总感觉为何我们调用旋转的函数,和物体有点不相关呢?
好,接下来,我们看看投影这块. 既然,已经转换到观察坐标系了,我们在观察坐标系的世界里,把物体投影在我们的观察平面的中,然后通过裁剪窗口,截取我们需要的那块就可以了.
我们这边以:透视投影为例, 它是怎样来达到这个效果呢?
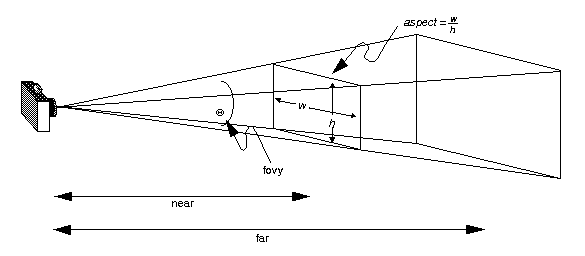
借用网上的这幅图片,我们来说明gluPerspective,是做什么的,为什么要这么做?
前面我们说过,透视投影,类似于一组聚焦的光线,把物体投影到我们的观察平面上.
现在我们就在想,观察平面在那呢? 投影的聚焦的光线聚焦在那点呢?
如果知道了这个,也就好算,某个位置的点在观察平面上投影了.
Opengl规定,透视投影的聚焦点,在观察坐标系的原点(也就是我们gluLooKAt的指定的观察点),那我们的观察平面在哪呢?裁剪窗口又在哪呢?
这就是opengl里面的gluPerspective要实现的.
gluPerspective(GLdouble fovy,GLdouble aspect,GLdouble zNear,GLdouble zFar)
zNear,zFar是到观察原点的距离(沿着z的负轴方向),因此这两个数应该总数设定成正数.
从网上很多资料都在说,zNear和zFar做为一个深度的裁剪范围,在这个范围内的物体才能进行投影,否则就直接忽略.初学者到这个地方,也能够理解,但从我们上面的问题来看,我们不知道观察平面在哪呢? 其实opengl已经规定了,观察平面就在近平面这里,也就是zNear指定的地方, 观察平面是平行于观察坐标系的(X,Y),因此我们指定z轴,也就指定它的位置.
OK,我们的观察平面已经确定了,那观察平面的裁剪区域呢?
前面我们说过,观察平面的裁剪窗口的 横纵比(w/h)最好和屏幕的一致(估计说的不准确,也就是视口的横纵比,从而只是等比例缩放而已). 因此,gluPerspective的第二个参数就是 aspect了,这样就把裁剪区域的宽度和高度的比例确定了.那剩下的是,我们目前还需要设定高度或者宽度.
gluPerspective的第一个参数是,fovy,它是一个角度.其实通过fovy和zNear能够计算出裁剪窗口的高度.从而我们也就决定了裁剪窗口
的大小了. fovy就是视锥体的上下平面的角度. 裁剪窗口的高度 h = 2 * tan(fovy/2) * zNear.
从而我们也就明白了,上面有个网页上,把它比如成眼睛的睁开度,感觉有点牵强.
从而我们知道,如果它为0的话,那肯定裁剪窗口的高度和宽度都为0,那就没有任何显示了.呵呵
如果它是180度,那就是裁剪窗口的高度就是无穷大,肯定没有实际价值,程序有可能也崩溃了.
如果是178度,那它的裁剪窗口的高度也很大,裁剪的窗口越大,也就意味着它显示的东西越多. 如果对于同一个物体成像来说,它在观察平面的投影是不变的. 但由于底片的大小比我们视口的大,那我们就要等比例缩放了,从而在屏幕上的显示时,我们就感觉它变小了.呵呵.
上面网页上,还有一个截图,如果设置成1度,在很远的地方的一个球,感觉看的很大,很清楚,类似于照相机的镜头拉近了.
它也是一样的原理,本身这个球,在1度还是90度,在我们的观察平面的投影是不变的,而变换的是我们的裁剪窗口的大小.设成1度,基本上裁剪窗口的高度很小,从而我们放到视口上,它就必须同比例的放大.从而就感觉放大了.并且显示的场景的范围也变小了.
好了,到目前位置,我们也就说清楚了gluLooKAt 和 gluPerspective的作用了,还有什么不明白的,请评论?谢谢
视口的调整大小,opengl的函数是glViewPort,这个和二维的就一样了,没有特别需要注意的.