胡乱记了点,方便以后复习
8.6没记
8.7有点少
今天讲的数论和数据结构,上午讲的内容,上课的老师认为“友好”;
我。。
其实听的还可以,毕竟之前学过,exgcd和线性筛和exgcd求逆元;
Exgcd()
是求解ax+by = gcd(a,b)的算法
Ax + by = m当且仅当m%gcd(a,b) == 0时有解
因为gcd(a,b) == gcd(b,a %b)
所以只要我们找到bx2+(a%b)y2==gcd(b,a%b)
就可以
A%b ==a – a/b*b
所以bx2+(a%b)y2 ay2+b(x - a / b * y)
当b0时x=1是方程解,然后回溯
欧拉筛
for(int i=2; i<=n; i++){
if(!vis[i]) prime[cnt++]=i;
for(int j = 0; j < cnt && i * prime[j] <= n; j++){
vis[i * prime[j]]=prime[j];
if(i % prime[j] == 0) break; //防止一个数不是被他的最小因子筛掉
//例如如果没有这句,12会被i==4,j==2时筛掉,但实际上应该被i==6,j==1时筛掉
}
}
欧拉筛不仅可以筛素数还可以求最小质因子
逆元
如果AB % M = 1
那么A、B互为在模M下的逆元
如果A、M不互质,那么A不存在模M下的逆元。
AB%M == AB+MY
Int mod_inverse(int a, int m){
Int x, y;
Exgcd(a, m, x, y);
Return (x % m + m) % m;
}
但是后面的题目都是英文不说(老师翻译了),还没什么思路,
下午讲的数据结构可能是老师预计的没讲完,讲的二叉堆,二叉搜索树,线段树,树状数组
和几道题目,相比数论还是好很多的
下午的题目至少还听懂了好几道,但是只实现出了一个,而且没有oj评测和数据点,然后下午大部分时间在写一道上古时代就应该会的题
迪杰斯特拉堆优化
然后一直没写出来,最后理解了但是还是不过,我吧我看的那篇题解代码沾上去也不过。。。。。我一脸懵,我写了这么长时间怎么不对。。。
8.8
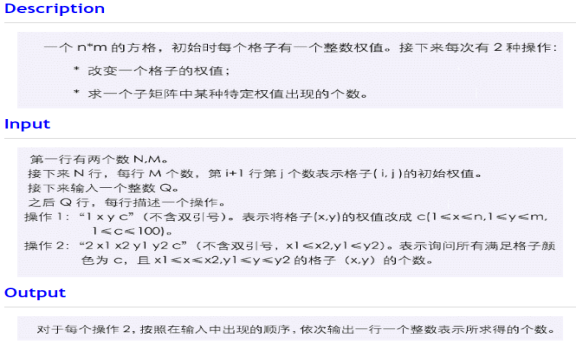
用什
二维树状数组
•void add(int x,int y, int val)
•{
• for(int i=x;i<=n;i+=lowbit(i))
• for(int j=y;j<=m;j+=lowbit(j))
• s[i][j]+=val;
•}
都是加一维(以添加为例)
并查集
路径压缩
Find(int x){return x == fa[x] ? x : f[x] = find(f[x])}
按秩合并
对于每个并查集维护一个size数组,每次合并两个数组时将小的合并到大的上
X = find(x);y = find(y);
If(size[x] > size[y]) {fa[y] = x;size[x] += size[y]};//初始化时令每一个size=1;
Else{fa[x] = y;size[y] += size[x]};
只写路径压缩复杂度就很低,很难被卡掉,不过卡常的时候可以用按秩合并
关押罪犯
(做过,讲过不知道多少遍的题......)
1.二分答案将<当前答案的边连起来,判断是否为二分图(黑白染色法)
//二分图判定
vector<int> e[N];
int col[N]; //col[u]表示u的颜色,1为白色,-1为黑色,0为未染色
bool flag=true; //是否为二分图
void dfs(int u,int c) {
col[u]=c;
for(int i=0;i<e[u].size();++i) {
int v=e[u][i];
if(!col[v]) dfs(v,-c);
else if(col[v]==c) flag=false;
}
}
for(int i=1;i<=n;++i)
if(!col[i]) dfs(i,1);
by老师
2.从大到小排序边(两人的怒气值),每次如果x和没有敌人,就将x的敌人设成y,否则就将x和y的敌人放到同一个并查集,代表在同一个监狱,y和x操作相同
当我们发现当前枚举的边关系的两个人x,y已经在同一集合,我们虽然有可能通过其他方式使他们不在同一集合,但那样会使其他更大的边连起来(因为我们从大到小枚举,枚举当前边之前其他边已经要求并查集就是这样,所以我们只能让这件事发生,他们的影响力即为答案)
星球大战
由于并查集不支持删边操作,但是并没有强制在线
我们可以倒着加边,即先求最后删完边,再加一条边(倒数第二个删的边)
求倒数第二个情况,以此类推
例8
一个无相连通图,每条边都有权值,两个点互相到达的代价是他们经过路径的最大权值
每次询问
输出所有互相到达代价小于k的两个城市
离线处理,按k值从小到大排序,是一个加边的过程,用并查集维护连通块
Trie字典树
用二维数组存ch[n][m]n代表最长串的长度,m代表每一个串的每一个字符有多少不同的情况
例如:每一个都是小写字母组成的字符串m就是26
插入:
初始化
O = 0;
查看字符串中第i个字符有没有在o的后面现过(即ch[o][第i点]是否不等于0)
,出现过就让”指针”o = 当前节点的标号
没有就新建一个点ch[o][当前点]=++cnt,o = cnt
`i++,重复以上操作
例9
给定n个数求出其中两个数异或最大值
将所有的数补至30位(2进制)(为了从最高位比较),然后放到踹树里(二进制)
每次选取一个数,在踹树上匹配,因为我们从最高位匹配,所以如果现在我们可以选择0或1
(1)当前选择1的话假设以后都是最坏情况(即每次都只能选0)异或后答案是1后面全是0
(2)和当前选0的话以后都是最好情况(即每次都能选1)大啊是0后面全是1
所以我们看出当前选1的话无论如何都会优于选0,所以每次贪心选,(当然,如果没有1只能选0),把n个数都[]跑完之后去max
例十
•维护一个数据结构,支持:
•1.插入一个正整数x(x<=10^9)
•2.询问已插入的数中有多少个与y异或得到的结果>=z(y,z<=10^9)
•操作数<=10^5
查询的时候,比如说我们要求结果大于10011,我们当前如果走1这条路最差是1000000(比10011大),这棵树就不需要递归了,直接加上这颗树的大小(需要记一个size数组)
当前选0的话最好情况是01111(小于10011),我们也不需要递归,因为永远得不到我们想要的结果,直接忽略,这样比暴力忧很多
例11
这个改题面为查询的时候p没有限制
维护每个点的前缀和,放到踹树中,所有数的异或和为sum,每次找与x^sum异或后的最大值,
因为a^a = 0,所以将sum和某一个前缀异或得到的就是当前位置开始的后缀
St表
倍增的思想,解决的是,RMQ问题(即某一区间的最大或最小值)
F[i][j]代表从i开始的2的j次方个节点的最值
F[i][j] = max(f[i][j – 1],f[f[i][j - 1]+ 1][j - 1])
即第i个节点开始到第2的j次方后的节点的最值=max(i开始第2的j-1次方的最值,i开始第2的j – 1次方开始再2的j – 1次方的最值)
即,一个区间最值 = max(他左一半的最值,右一半的最值)
比如1到4的区间最值(f[1][2]) = 1到2最值(f[1][1])和3到4最值(f[3][1])中大的那个
LCA的三种解决方式
1倍增:
F[i][j]代表第i个节点向上第2的j次方后的节点
F[i][j] = f[f[i][j – 1]][j - 1]
即第i个节点向上第2的j次方后的节点=(第i个节点向上跳2的j – 1次方后的节点)再向上跳2的j – 1 次方的节点
因为2的j – 1次方加2的j – 1次方 = 2的j次方
2转换RMQ问题
某个巨佬已经证明出RMQ和LCA可以互相转换.
(1)求出树的dfs序
(2)两个点u,v的LCA是pos[u]到pos[v]中深度最小的点
Ps:pos[x]代表x在dfs中个出现的顺序,u代表较早出现的点,v和u相反
3用tarjan算法
然而我并不会tarjan...
•①记录每个点的询问
•②dfs回溯时用并查集合并(将子结点集合并到父节点集合,以父节点为根)
•③查询lca(u,v)时假设此时u已访问,v刚访问到,那么u的并查集的根即为答案
强行复制,逃.
Hash
哈希容易出现哈希碰撞,可以使用无错哈希
开m个vector(m为哈希的模数),每次遇到相同模数的时候将当前值放进去,每个点的期望还是O(1),所以对空间和时间影响不大
双模哈希理论可以被卡,但是非常困难,所以可以用,如果被卡了就是脸黑木办法hhh
即每一个数模两个不同的数,只有两个模数都相同,才能证明出现过
哈希还可以用来记录状态,比如八数码问题使得判重只需要O(1)
8.9今天听得也不咋地
图论
克鲁斯卡尔算法证明
N==1时,最小生成树显然
在n == k成立时,n == k + 1有一条边(u,v)是连接新节点的最短边,因为需要构成一颗树,所以,这个点一定要连出一条边,假设不是最短边,我们就将最短边连起来,在一棵树中连一条不重复的边会构成环,那么环中任意删除一条边还是树,所以,连上最短边再删除一条环中边肯定更优
例1
N个村庄,每个村庄要么打一口井,要么从某一个有水的地方建一个管道,问最小代价
有水☞
(1)村庄建了井
(2)村庄向有水的地方建了一个管道
建另一个节点0为”水井”,他和每一个节点连边,边权为节点建水井的费用
这样只要求最小生成树即可
货车运输
方法一
克鲁斯卡尔算法
用克鲁斯卡尔算法求最大生成树,
用倍增求LCA,顺便求出路径最小值
方法二
Kruskal重构树
在kruskal的过程中
若当前边所连两点u和v不在一个集合内
则新建一个节点node,点权为该边边权
然后连接u所在集合的根与node以及v所在集合的根与node
重构完成之后,指定每个集合的根作为所在森林的根
则u到v路径上最大边权的最小值 就是LCA(u,v)的点权
强行复制,逃.
例3舒适的路线
给定一张图,n个点,m条边,求一棵生成树,满足它的边权最小值最大。输出这个最小值
直接用克鲁斯卡尔求最大生成树
另一个方法 玄学 && 找”出阿宝”做法,二分答案
Spfa算法判负环,
我不管了.....弄了半天也没搞懂原理,反正就是每个点进队n - 1次就说明有负环
也有dfs的做法,每次枚举每一个点,每次走负边(1到2是-2,2到3是1也算负边),如果一个点再次被搜到,就说明有负环
Tarjan算法
Dfn[n]代表点n第几次搜到
low[n]代表n及n搜索树子树中的点中能访问到的点dfn的最小值
自己写个伪代码
塔尖(int x){
标记为x访问过
For遍历每一条边(递归每个子树)
如果当前节点没有访问过
递归子树根节点
Low[x]取x和子树根最小值
否则
Low[x]和子树根的low取min
}
如果dfs[n] == low[n]
记录强连通分量个数的变量++
将栈中全部元素弹出,标记vis[元素] = n代表这些元素在这个强连通分量里
间谍网络
我们已知的某些受贿的间谍,和他们需要的钱。我们还知道哪些间谍手中具体掌握了哪些间谍的资料。假设总共有n个间谍(n不超过3000),每个间谍分别用1到3000的整数来标识。
请根据这份资料,判断我们是否有可能控制全部的间谍,如果可以,求出我们需要支付的最少资金。否则,输出不能被控制的一个间谍。
首先tarjan缩点(以下是有解的情况),
对于没有环的图,我们选择入度为零的人进行贿赂,其余有入度的人都会被揭发
对于有环的图,我们塔尖缩点,就变成了有向无环图,这个点的代价就是需要最少钱被贿赂的那个人需要的钱
差分约束
差分约束系统由形如xi - xj <= k这样的式子组合而成,
求xs - xt最大值
求解方法:
(1)将形式变成xi - xj <= k
(2)令xj向xi连一条长度为k的边
(3)求出s到t的最大值
图中有负环则解不存在,无法互相到达则答案为无限大(因为没有什么限制他)
今天其实听得不怎么好,有很多东西没有记下来
8.11
动态规划
状态与记忆化搜索
状态其实就是问题的子问题
记忆化搜索 vs 动态规划
无需考虑顺序 需要考虑顺序
容易实现,容易理解 不容易实现,不容易理解
常数大 常数小
优化困难 部分容易优化
线性动态规划
小齐挖矿
现在有m + 1个星球,从左到右标号为0到m,小奇最初在0号星球。
有n处矿体,第i处矿体有ai单位原矿,在第bi个星球
每次只能调到x + 4或x + 7的位置,问最多挖多少矿
通过%#$@^%@!可以发现,两个星球只要相隔距离大于17,就一定能到达
所以我们把所有距离相隔大于17的星球距离设为18,这样就只需要18 * n的空间
以及只需要18 * n的时间
大搬家
现在有一个长度为n的搬家指示,其中ai表示住在第i栋房子的人需要搬家到第ai栋房子
N家连续搬家,结果,第3次搬家结果跟第一次结果相同
问有多少种不同的数列答案对1000000007取模
最大子矩阵
有一个n*2的矩阵,请你选出其中k个子矩阵,使得这
个k个子矩阵分值之和最大。子矩阵不能互相重叠
状态太多直接复制ppt上的吧
定义状态
fi,j表示前i行,选了j个子矩阵,当前两列不属于任何矩阵的最大值。
gi,j表示前i行,选了j个子矩阵,当前两列属于同一个矩阵的最大值。
hi,j表示前i行,选了j个子矩阵,当前两列属于不同矩阵的最大值。
si,j表示前i行,选了j个子矩阵,左边一列属于一个矩阵的最大值。
ti,j表示前i行,选了j个子矩阵,右边一列属于一个矩阵的最大值.
玩具取名
名字是从”WING”四个字母中选出一个,然后经过一系列变化变成名字
区间dp,设f[i][j]][k]为i 到j这个区间k能不能被合成
每次枚举区间时,枚举每一个变化方案,看看能否由小的区间合并成这个区间
染色
长度为n的木板每次课选择一个连续的区间染色,后染的会覆盖先染的
问最少染几次
F[i][j] 表示i到j的区间染色的最小值
如果a[i] == a[i + 1] 那么f[i][j] = f[i + 1][j]
如果a[j - 1] == a[j] 那么f[i][j] = f[i][j - 1]
如果a[i] == a[j] 那么 f[i][j] = f[i + 1][j],f[i][j - 1],f[i][j]
除了这些以外,f[i][j] = f[i][mid]+f[mid + 1][j]
以上式子都要取min
然后大多数题都没记笔记,实际因为都不会,晚上剩下的时间做了一道区间dp,加深理解吧(这道题难度远远低于今天讲的题目的难度)