Minimum Height Trees (M)
题目
A tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree.
Given a tree of n nodes labelled from 0 to n - 1, and an array of n - 1 edges where edges[i] = [ai, bi] indicates that there is an undirected edge between the two nodes ai and bi in the tree, you can choose any node of the tree as the root. When you select a node x as the root, the result tree has height h. Among all possible rooted trees, those with minimum height (i.e. min(h)) are called minimum height trees (MHTs).
Return a list of all MHTs' root labels. You can return the answer in any order.
The height of a rooted tree is the number of edges on the longest downward path between the root and a leaf.
Example 1:
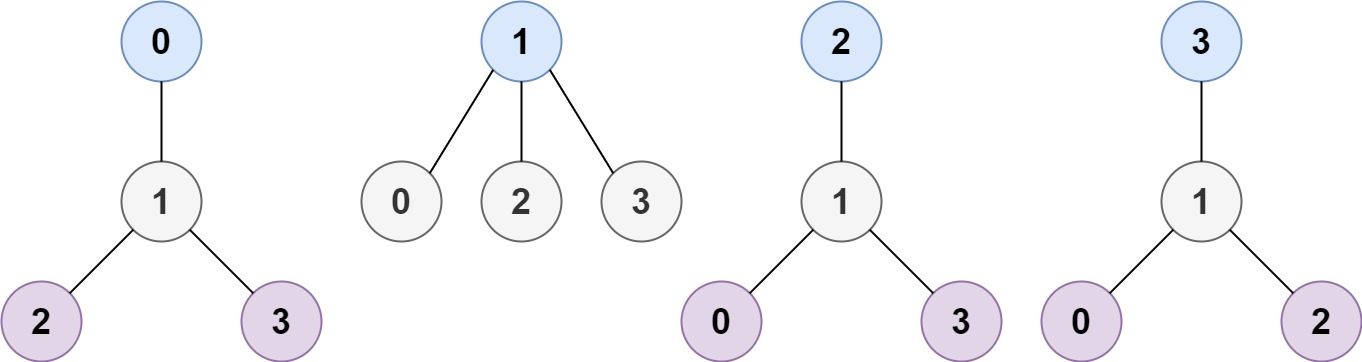
Input: n = 4, edges = [[1,0],[1,2],[1,3]]
Output: [1]
Explanation: As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.
Example 2:
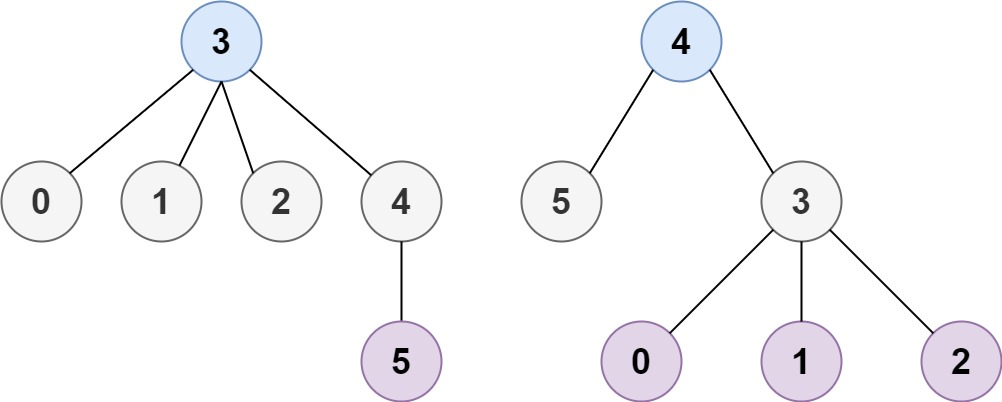
Input: n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
Output: [3,4]
Example 3:
Input: n = 1, edges = []
Output: [0]
Example 4:
Input: n = 2, edges = [[0,1]]
Output: [0,1]
Constraints:
1 <= n <= 2 * 10^4edges.length == n - 10 <= ai, bi < nai != bi- All the pairs
(ai, bi)are distinct. - The given input is guaranteed to be a tree and there will be no repeated edges.
题意
在给定的无向无环图中确定一个根结点,使得得到的树的高度最小。
思路
从最外层的叶结点开始一层一层向里面“剥”,直到只剩最里面的1或2个结点即为答案。具体方法是:根据信息构建图,并把所有叶结点加入到队列中;依次出队,删去叶结点,更新叶结点连接的所有结点,并将新生成的叶结点入队;重复直到只剩1或2个结点。
另一种可行的方法是,先求无向图的直径,即叶结点到叶结点的最长路径,再求这个路径中间的1或2个结点即为答案。求直径的具体方法:任选一个结点,用DFS/BFS找到离它最远的结点A,再从A出发,找到离A最远的结点B,A-B构成的路径即为直径。
代码实现
Java
class Solution {
public List<Integer> findMinHeightTrees(int n, int[][] edges) {
if (n == 1) {
return new ArrayList<Integer>() {
{
add(0);
}
};
}
Map<Integer, Set<Integer>> g = new HashMap<>();
Queue<Integer> q = new LinkedList<>();
for (int i = 0; i < edges.length; i++) {
int a = edges[i][0], b = edges[i][1];
g.putIfAbsent(a, new HashSet<>());
g.putIfAbsent(b, new HashSet<>());
g.get(a).add(b);
g.get(b).add(a);
}
for (int i = 0; i < n; i++) {
if (g.get(i).size() == 1) {
q.offer(i);
}
}
while (n > 2) {
int size = q.size();
for (int i = 0; i < size; i++) {
int x = q.poll();
for (int y : g.get(x)) {
g.get(y).remove(x);
if (g.get(y).size() == 1) {
q.offer(y);
}
}
}
n -= size;
}
return new ArrayList<>(q);
}
}