K近邻算法（一）：基本使用

一：K近邻算法

二：实际例子

(1) 判断电影类型

给一组电影，对应是打斗和接吻两个特征值来判断电影类型

import pandas as pd

rowdata = {"电影名称":["无问西东","后来的我们","前任3","红海行动","唐人街探案","战狼2"],
           "打斗次数":[1,5,12,108,112,115],
           "接吻次数":[101,89,97,5,9,8],
           "电影类型":["爱情片","爱情片","爱情片","动作片","动作片","动作片"]}
# 1.将字典格式，转换为能够处理的数据表格
movie_data = pd.DataFrame(rowdata)
print(movie_data)

#

电影名称 打斗镜头 接吻镜头 电影类型
0 无问西东 1 101 爱情片
1 后来的我们 5 89 爱情片
2 前任3 12 97 爱情片
3 红海行动 108 5 动作片
4 唐人街探案 112 9 动作片
5 战狼2 115 8 动作片

对应的用图像去描述的话

from matplotlib import pyplot as plt
x =  [1,5,12,108,112,115]
y =  [101,89,97,5,9,8]

# 画散点图，x和y里面的对应索引元素组成(x,y)
plt.scatter(x,y,s=80)

x1 = [24]
y1 = [67]
# market：表示点的形状  s：表示点的大小
plt.scatter(x1,y1,marker="^",s=80)
plt.show()

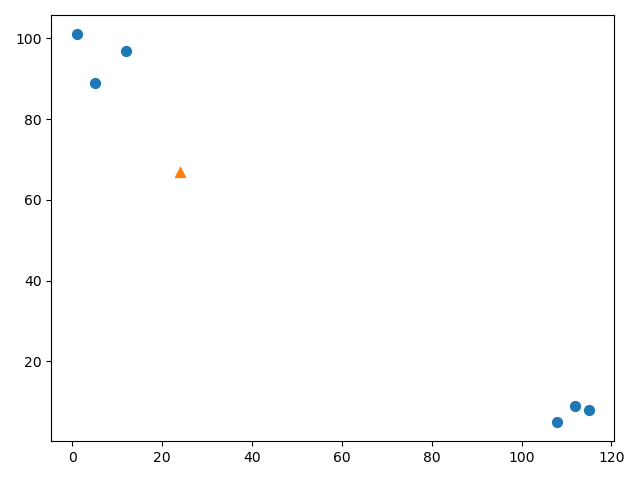
从图中可以看出，左上角的圆都代表爱情电影，右下角的圆都代表动作电影。图中的三角形，表示要分类的电影。

应为是两个特征值，二维平面就计算点与点的距离，计算结果如下

target_data = {"name":"猜猜看","type":"未知","data":(24,67)}
origin_data_list = [{"name":"无问东西","type":"爱情片","data":(1,101)},
                    {"name":"后来的我们","type":"爱情片","data":(5,89)},
                    {"name":"前任3","type":"爱情片","data":(12,97)},
                    {"name":"红海行动","type":"动作片","data":(108,5)},
                    {"name":"唐人街探案","type":"动作片","data":(112,9)},
                    {"name":"战狼2","type":"动作片","data":(115,8)}]

for info in origin_data_list:
    result = cmath.sqrt((info.get("data")[0]-target_data.get("data")[0]) ** 2 + (info.get("data")[1]-target_data.get("data")[1]) ** 2)
    print(target_data.get("name")+"距离" + info.get("name")+":" +str(result))


# 结果
猜猜看距离无问东西:(41.048751503547585+0j)
猜猜看距离后来的我们:(29.068883707497267+0j)
猜猜看距离前任3:(32.31098884280702+0j)
猜猜看距离红海行动:(104.4030650891055+0j)
猜猜看距离唐人街探案:(105.39449701004318+0j)
猜猜看距离战狼2:(108.45275469069469+0j)

距离猜猜看最近电影是后来的我们，类型是爱情片，如果我们根据这种形式进行判断的话，就叫做最近邻算法（KNN：k-nearest neighbor）。

第一步：K就是判定你要选择离你最近的几个点，假如我们选择K为5，那么离猜猜看最近的距离前五位分别是（29，32，41，104，105）

第二步：最近的几个点进行投票，票数多久的一方获胜，猜猜看就属于这一方，爱情片3票，概率为60%，动作片2票，概率为40%，所以猜猜看就属于爱情片。

完整的代码

import pandas as pd
rowdata = {"电影名称":["无问西东","后来的我们","前任3","红海行动","唐人街探案","战狼2"],
           "打斗镜头":[1,5,12,108,112,115],
           "接吻镜头":[101,89,97,5,9,8],
           "电影类型":["爱情片","爱情片","爱情片","动作片","动作片","动作片"]}
# 1.将字典格式，转换为能够处理的数据表格
movie_data = pd.DataFrame(rowdata)
# 2.计算已知类别和当前点的距离
new_data = [24,67]
# 对已知类别的数据进行处理 distance = movie_data.iloc[:6,1:3] # pandas数据格式,iloc(行,列)切割方法
# 切割的结果
打斗镜头  接吻镜头
0     1   101
1     5    89
2    12    97
3   108     5
4   112     9
5   115     8
distance = ((distance - new_data)**2)
print(distance)
# 打印的结果是
打斗镜头  接吻镜头
0   529  1156
1   361   484
2   144   900
3  7056  3844
4  7744  3364
5  8281  3481
distance = distance.sum(1)
print(distance)
# 打印的结果是
0     1685
1      845
2     1044
3    10900
4    11108
5    11762
print(list(distance**0.5))
# 打印的结果是
dtype: int64
[41.048751503547585, 29.068883707497267, 32.31098884280702, 104.4030650891055, 105.39449701004318, 108.45275469069469]

# 3. 对距离进行升序排序
distance = list(disctance**0.5)
distance_1 = pd.DataFrame({"distance":distance,"lable":(movie_data.iloc[:6,3])})
print(distance_1)
# 结果
    distance lable
1   29.068884   爱情片
2   32.310989   爱情片
0   41.048752   爱情片
3  104.403065   动作片
4  105.394497   动作片
5  108.452755   动作片
sort_disctance_1 = distance_1.sort_values(by="distance")  # 默认升序
print(sort_disctance_1)
# 结果
 distance lable
1   29.068884   爱情片
2   32.310989   爱情片
0   41.048752   爱情片
3  104.403065   动作片
4  105.394497   动作片
5  108.452755   动作片
sort_disctance_1 = sort_disctance_1[:5] # 因为k选取的5，因此取前五近的的距离
print(sort_disctance_1)
# 结果
  distance lable
1   29.068884   爱情片
2   32.310989   爱情片
0   41.048752   爱情片
3  104.403065   动作片
4  105.394497   动作片
# 4.进行概率统计
result = sort_disctance_1.loc[:,"lable"]
print(result)
# 结果是
1    爱情片
2    爱情片
0    爱情片
3    动作片
4    动作片
result = result.value_counts()
print(result)
# 结果是
Name: lable, dtype: object
爱情片    3
动作片    2
result = result.index
print(result)
# 结果是
Name: lable, dtype: int64
Index(['爱情片', '动作片'], dtype='object')
result = result[0]
print("电影的分类为:",result)
# 结果是
电影的分类为: 爱情片

封装成函数

def classify(new_data,dataSet,k):
    """
    函数功能：KNN分类器
    参数说明
    :param new_data: 需要预测的分类数据集
    :param dataSet: 已知分类标签的数据集(训练集)
    :param k: K-近邻算法参数，选择距离最近的k个点
    :return: 分类结果
    """
    result = list()
    distance = list((((dataSet.iloc[:,1:3]-new_data)**2).sum(1)) ** 0.5)
    distance_sort = pd.DataFrame({"distance":distance,"lable":dataSet.iloc[:,3]})
    distance_sort = distance_sort.sort_values(by="distance")[:k]
    ret = distance_sort.loc[:,"lable"].value_counts()
    result.append(ret.index[0])
    return result

if __name__ == '__main__':
    rowdata = {"电影名称": ["无问西东", "后来的我们", "前任3", "红海行动", "唐人街探案", "战狼2"],
               "打斗镜头": [1, 5, 12, 108, 112, 115],
               "接吻镜头": [101, 89, 97, 5, 9, 8],
               "电影类型": ["爱情片", "爱情片", "爱情片", "动作片", "动作片", "动作片"]}
    movie_data = pd.DataFrame(rowdata)
    new_data = [24,67]
    k = 3
    result = classify(new_data,movie_data,k)
    print(result)

# 结果
['爱情片']

（2）海伦约会实例

import pandas as pd
data_test = pd.read_table("datingTestSet2.txt",header=None)
data = data_test.head()

print(data)
print(data_Test.shape)

# 结果
       0          1         2  3
0  40920   8.326976  0.953952  3
1  14488   7.153469  1.673904  2
2  26052   1.441871  0.805124  1
3  75136  13.147394  0.428964  1
4  38344   1.669788  0.134296  1
(1000, 4)  # 数据总共有1000条

第一列：每年飞行历程
第二列：玩游戏所占比例
第三列：每周消费的冰淇淋公升数 
第四列：态度，1-不喜欢 2-一般喜欢 3-非常喜欢

数据展示

import matplotlib as mlp
import matplotlib.pyplot as plt

# 不同标签区分颜色
label_color = []
for i in range(data_test.shape[0]):
    label_number = data_test.iloc[i,-1]
    if label_number == 1:
        label_color.append("black")
    elif label_number == 2:
        label_color.append("orange")
    else:
        label_color.append("red")

# 设置两两特征值之间的散点图
plt.rcParams["font.sans-serif"] = ["Simhei"]  # 字体设置为黑体
# 总画布的大小
pl = plt.figure(figsize=(12,8))
# 区域一的大小
fig1 = pl.add_subplot(221)
plt.scatter(data_test.iloc[:,1],data_test.iloc[:,2],marker=".",c=label_color)
plt.xlabel（"游戏时间占比"）
plt.ylabel（"每周消耗冰淇淋公升数"）
plt.show()

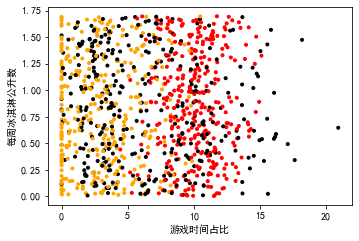
同样的可以画出其余两张图

fig1 = pl.add_subplot(222)
plt.scatter(data_test.iloc[:,0],data_test.iloc[:,1],marker=".",c=label_color)
plt.xlabel("飞行公里数")
plt.ylabel("游戏时间占比")

fig1 = pl.add_subplot(222)
plt.scatter(data_test.iloc[:,0],data_test.iloc[:,2],marker=".",c=label_color)
plt.xlabel("飞行公里数")
plt.ylabel("每周冰淇淋公升数")
plt.show()

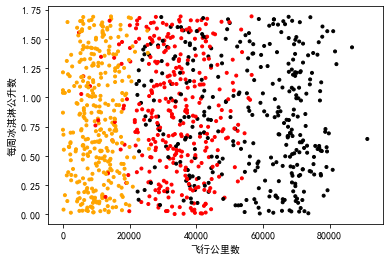
str is not  'str' object is not callable，重启jupyter notebook即可

从三张图可以看出，飞行公里数和游戏时间占比对结果影响较大。假如三个特征同等重要，那么就要对三个特征进行归一化处理，让她们的权重相等。

归一化的方法有：0-1标准化，Z-score标准化，Sigmoid压缩法等

def one_zero(dataset):
    mindf = dataset.min()
    maxdf = dataset.max()
    normset = (dataset-mindf)/(maxdf-mindf)
    return normset


datingT = pd.concat([one_zero(data_test.iloc[:,:3]),data_test.iloc[:,3]],axis=1)
datingT.head()

# 结果
          0         1         2  3
0  0.448325  0.398051  0.562334  3
1  0.158733  0.341955  0.987244  2
2  0.285429  0.068925  0.474496  1
3  0.823201  0.628480  0.252489  1
4  0.420102  0.079820  0.078578  1

分测试集合训练集

# 3.分测试集合训练接，使用0-1标准化
def randomSplit(dataset,rate=0.9):
    n = dataset.shape[0]
    m = int(n*rate)
    train = dataset.iloc[:m,:]
    test = dataset.iloc[m:,:]
    test.index = range(test.shape[0])
    return train,test


train,test = randomSplit(datingT)
print(train.head())
print("---"*20)
print(test.head())

# 结果
0  0.448325  0.398051  0.562334  3
1  0.158733  0.341955  0.987244  2
2  0.285429  0.068925  0.474496  1
3  0.823201  0.628480  0.252489  1
4  0.420102  0.079820  0.078578  1
------------------------------------------------------------
          0         1         2  3
0  0.513766  0.170320  0.262181  1
1  0.089599  0.154426  0.785277  2
2  0.611167  0.172689  0.915245  1
3  0.012578  0.000000  0.195477  2
4  0.110241  0.187926  0.287082  2

import pandas as pd
# 1.数据准备
data_Test = pd.read_table("datingTestSet2.txt",header=None)
# data = data_Test.head()
# print(data)
# print(data_Test.shape)
# print(data_Test.info())

# 2.数据展示
import matplotlib as mlp
import matplotlib.pyplot as plt

# 不同标签区分颜色
# label_color = []
# for i in range(data_Test.shape[0]):
#     label_number = data_Test.iloc[i,-1]
#     if label_number == 1:
#         label_color.append("black")
#     elif label_number == 2:
#         label_color.append("orange")
#     else:
#         label_color.append("red")

# 设置两两特征值之间的散点图
# plt.rcParams["font.sans-serif"] = ["Simhei"]  # 字体设置为黑体
# 总画布的大小
# pl = plt.figure(figsize=(12,8))

# 区域一的大小
# fig1 = pl.add_subplot(221)
# plt.scatter(data_Test.iloc[:,1],data_Test.iloc[:,2],marker=".",c=label_color)
# plt.xlabel("游戏比例")
# plt.ylabel("每周消耗冰淇淋公升数")
# plt.show()

def one_zero(dataset):
    mindf = dataset.min()
    maxdf = dataset.max()
    normset = (dataset-mindf)/(maxdf-mindf)
    return normset


datingT = pd.concat([one_zero(data_Test.iloc[:,:3]),data_Test.iloc[:,3]],axis=1)


# 3.分测试集合训练接
def randomSplit(dataset,rate=0.9):
    n = dataset.shape[0]
    m = int(n*rate)
    train = dataset.iloc[:m,:]
    test = dataset.iloc[m:,:]
    test.index = range(test.shape[0])
    return train,test


train,test = randomSplit(datingT)


def datingClass(train,test,k):
    n = train.shape[1] - 1
    m = test.shape[0]
    result = []
    for i in range(m):
        dist = list((((train.iloc[:,:n] - test.iloc[i,:n])**2).sum(1))**2)
        dist_l = pd.DataFrame({"dist":dist,"labels":(train.iloc[:,n])})
        dr = dist_l.sort_values(by="dist")[:k]
        ret = dr.loc[:,"labels"].value_counts()
        result.append(ret.index[0])
    result = pd.Series(result)
    test["predict"] = result
    accurate = (test.iloc[:,-1] == test.iloc[:,-2]).mean()
    print("预测的准确性为:{}".format(accurate))
    print("_"*100)
    return test


result = datingClass(train,test,4)

# 结果
预测的准确性为:0.93

Z-score标准化的预测准确性

import pandas as pd
# 1.数据准备
data_Test = pd.read_table("datingTestSet2.txt",header=None)


def z_score(dataset):
    count = dataset.shape[0]
    total_1 = sum(dataset.iloc[:,0])
    total_2 = sum(dataset.iloc[:,1])
    total_3 = sum(dataset.iloc[:,3])
    ave_1 = total_1/count
    ave_2 = total_2/count
    ave_3 = total_3/count
    sd_1 = ((sum([(dataset.iloc[i,0]-ave_1)**2 for i in range(count)]))/count)**0.5
    sd_2 = ((sum([(dataset.iloc[i,1]-ave_2)**2 for i in range(count)]))/count)**0.5
    sd_3 = ((sum([(dataset.iloc[i,2]-ave_3)**2 for i in range(count)]))/count)**0.5
    dataset.iloc[:,0] = (dataset.iloc[:,0] - ave_1)/sd_1
    dataset.iloc[:,1] = (dataset.iloc[:,1] - ave_2)/sd_2
    dataset.iloc[:,2] = (dataset.iloc[:,2] - ave_3)/sd_3
    return dataset

data_normal = z_score(data_Test)
# 样子是
   0         1         2  3
0    0.331932  0.416602 -0.821235  3
1   -0.872478  0.139929 -0.247790  2
2   -0.345549 -1.206671 -0.939778  1
3    1.891029  1.553092 -1.239391  1
4    0.214553 -1.152936 -1.474096  1
..        ...       ...       ... ..
995 -1.024806 -0.742505 -1.077801  2
996  1.604417  0.805083 -1.047574  1
997 -0.321718  0.964316 -0.890790  3
998  0.659599  0.606995 -1.001172  3
999  0.461203  0.311833 -0.519763  3

[1000 rows x 4 columns]

print(data_normal)

# 3.分测试集合训练接
def randomSplit(dataset,rate=0.9):
    n = dataset.shape[0]
    m = int(n*rate)
    train = dataset.iloc[:m,:]
    test = dataset.iloc[m:,:]
    test.index = range(test.shape[0])
    return train,test

train,test = randomSplit(data_normal)


def datingClass(train,test,k):
    n = train.shape[1] - 1
    m = test.shape[0]
    result = []
    for i in range(m):
        dist = list((((train.iloc[:,:n] - test.iloc[i,:n])**2).sum(1))**2)
        dist_l = pd.DataFrame({"dist":dist,"labels":(train.iloc[:,n])})
        dr = dist_l.sort_values(by="dist")[:k]
        ret = dr.loc[:,"labels"].value_counts()
        result.append(ret.index[0])
    result = pd.Series(result)
    test["predict"] = result
    accurate = (test.iloc[:,-1] == test.iloc[:,-2]).mean()
    print("预测的准确性为:{}".format(accurate))
    return test


result = datingClass(train,test,4)
# 结果是
预测的准确性为:0.94

Sigmoid压缩法的预测准确性

# 后续加上

三：K近邻算法的局限性

算法的准确性与K的取值有关系

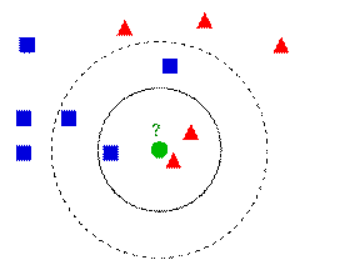
假如K取3的话，那么测试数据就属于三角形，假如k取5的话，测试数据就属于正方形。

K近邻算法的改进：https://blog.csdn.net/qq_36330643/article/details/77532161

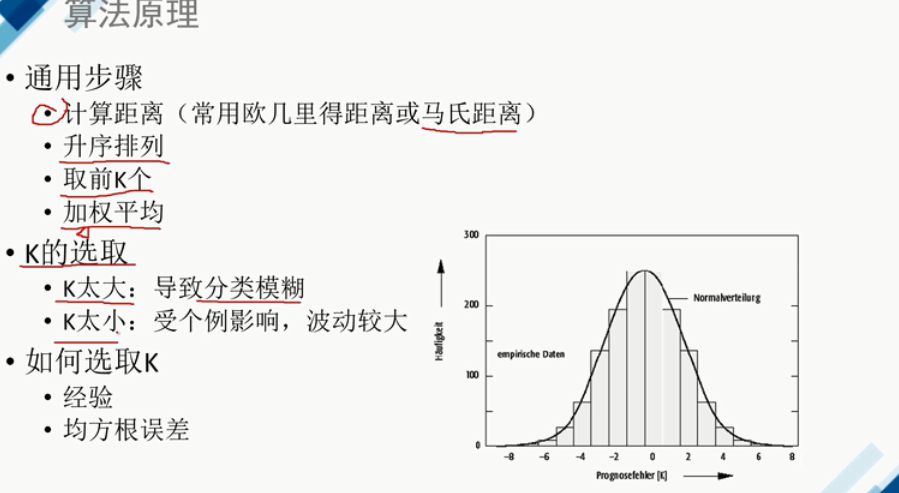
加权，距离近的权重高，距离远的权重低

数据集的下载和链接

链接：https://pan.baidu.com/s/1N1vS_iJps-ul89nmQDONDw
提取码：azdd

# TODO