Nam is playing with a string on his computer. The string consists of n lowercase English letters. It is meaningless, so Nam decided to make the string more beautiful, that is to make it be a palindrome by using 4 arrow keys: left, right, up, down.
There is a cursor pointing at some symbol of the string. Suppose that cursor is at position i (1 ≤ i ≤ n, the string uses 1-based indexing) now. Left and right arrow keys are used to move cursor around the string. The string is cyclic, that means that when Nam presses left arrow key, the cursor will move to position i - 1 if i > 1 or to the end of the string (i. e. position n) otherwise. The same holds when he presses the right arrow key (if i = n, the cursor appears at the beginning of the string).
When Nam presses up arrow key, the letter which the text cursor is pointing to will change to the next letter in English alphabet (assuming that alphabet is also cyclic, i. e. after 'z' follows 'a'). The same holds when he presses the down arrow key.
Initially, the text cursor is at position p.
Because Nam has a lot homework to do, he wants to complete this as fast as possible. Can you help him by calculating the minimum number of arrow keys presses to make the string to be a palindrome?
The first line contains two space-separated integers n (1 ≤ n ≤ 105) and p (1 ≤ p ≤ n), the length of Nam's string and the initial position of the text cursor.
The next line contains n lowercase characters of Nam's string.
Print the minimum number of presses needed to change string into a palindrome.
8 3 aeabcaez
6
A string is a palindrome if it reads the same forward or reversed.
In the sample test, initial Nam's string is: 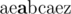 (cursor
position is shown bold).
(cursor
position is shown bold).
In optimal solution, Nam may do 6 following steps:
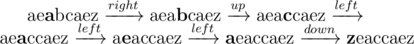
The result, 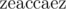 ,
is now a palindrome.
,
is now a palindrome.
分成两部分,一是字母的变换,一是位置的移动,仅仅考虑一半就可以。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
typedef long long LL;
using namespace std;
#define REPF( i , a , b ) for ( int i = a ; i <= b ; ++ i )
#define REP( i , n ) for ( int i = 0 ; i < n ; ++ i )
#define CLEAR( a , x ) memset ( a , x , sizeof a )
const int maxn=1e5+100;
char str[maxn];
int num[maxn];
int n,pos;
int main()
{
std::ios::sync_with_stdio(false);
while(cin>>n>>pos)
{
cin>>(str+1);
CLEAR(num,0);
int ans=0;
REPF(i,1,n/2)
{
if(str[i]!=str[n-i+1])
{
int tt=abs(str[i]-str[n-i+1]);
num[i]=min(tt,26-tt);
num[n-i+1]=min(num[i],26-num[i]);
ans+=num[i];
}
}
int l=n,r=1;
if(pos<=n/2)
{
REPF(i,1,n/2)
{
if(num[i])
{
l=min(l,i);
r=max(r,i);
}
}
}
else
{
REPF(i,n/2+1,n)
{
if(num[i])
{
l=min(l,i);
r=max(r,i);
}
}
}
if(l!=n)
{
if(pos<=l) ans+=r-pos;
else if(pos>=r) ans+=pos-l;
else ans+=min(r-l+r-pos,pos-l+r-l);
}
cout<<ans<<endl;
}
return 0;
}
The next "Data Structures and Algorithms" lesson will be about Longest Increasing Subsequence (LIS for short) of a sequence. For better understanding, Nam decided to learn it a few days before the lesson.
Nam created a sequence a consisting of n (1 ≤ n ≤ 105) elements a1, a2, ..., an (1 ≤ ai ≤ 105). A subsequence ai1, ai2, ..., aik where 1 ≤ i1 < i2 < ... < ik ≤ n is called increasing if ai1 < ai2 < ai3 < ... < aik. An increasing subsequence is called longest if it has maximum length among all increasing subsequences.
Nam realizes that a sequence may have several longest increasing subsequences. Hence, he divides all indexes i (1 ≤ i ≤ n), into three groups:
- group of all i such that ai belongs to no longest increasing subsequences.
- group of all i such that ai belongs to at least one but not every longest increasing subsequence.
- group of all i such that ai belongs to every longest increasing subsequence.
Since the number of longest increasing subsequences of a may be very large, categorizing process is very difficult. Your task is to help him finish this job.
The first line contains the single integer n (1 ≤ n ≤ 105) denoting the number of elements of sequence a.
The second line contains n space-separated integers a1, a2, ..., an (1 ≤ ai ≤ 105).
Print a string consisting of n characters. i-th character should be '1', '2' or '3' depending on which group among listed above index ibelongs to.
1 4
3
4 1 3 2 5
3223
4 1 5 2 3
3133
In the second sample, sequence a consists of 4 elements: {a1, a2, a3, a4} = {1, 3, 2, 5}. Sequence a has exactly 2 longest increasing subsequences of length 3, they are {a1, a2, a4} = {1, 3, 5} and {a1, a3, a4} = {1, 2, 5}.
In the third sample, sequence a consists of 4 elements: {a1, a2, a3, a4} = {1, 5, 2, 3}. Sequence a have exactly 1 longest increasing subsequence of length 3, that is {a1, a3, a4} = {1, 2, 3}.
两段LIS。进行推断:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<limits.h>
typedef long long LL;
using namespace std;
#define REPF( i , a , b ) for ( int i = a ; i <= b ; ++ i )
#define REP( i , n ) for ( int i = 0 ; i < n ; ++ i )
#define CLEAR( a , x ) memset ( a , x , sizeof a )
const int maxn=1e5+100;
int t1[maxn],t2[maxn],a[maxn],s[maxn];
int ans[maxn],h[maxn],mm;
int main()
{
int n;
std::ios::sync_with_stdio(false);
while(cin>>n)
{
mm=0;
REPF(i,1,n) cin>>a[i];
REPF(i,1,n)
{
s[i]=INT_MAX;
int tt=lower_bound(s+1,s+1+i,a[i])-s;//查找a[i]大于等于的元素的位置
t1[i]=tt;
s[tt]=a[i];
mm=max(mm,tt);
}
for(int i=n;i>=1;i--)
{
s[n-i+1]=INT_MAX;
int tt=lower_bound(s+1,s+n-i+2,-a[i])-s;
t2[i]=tt;
s[tt]=-a[i];
}
CLEAR(h,0);
REPF(i,1,n)
{
if(t1[i]+t2[i]-1<mm) ans[i]=1;
else { ans[i]=2; h[t1[i]]++;}
}
REPF(i,1,n)
{
if(ans[i]==2&&h[t1[i]]==1)
ans[i]=3;
}
REPF(i,1,n)
cout<<ans[i];
cout<<endl;
}
return 0;
}版权声明:本文博客原创文章,博客,未经同意,不得转载。