查找子字符串
Introduction
在长度为 N 的文本里寻找长度为 M 的模式(子串),典型情况是 N >> M。

这个应用就很广泛啦,在文本中寻找特定的模式(子串)是很常见的需求。
Brute Force
我们先来了解一下暴力查找。
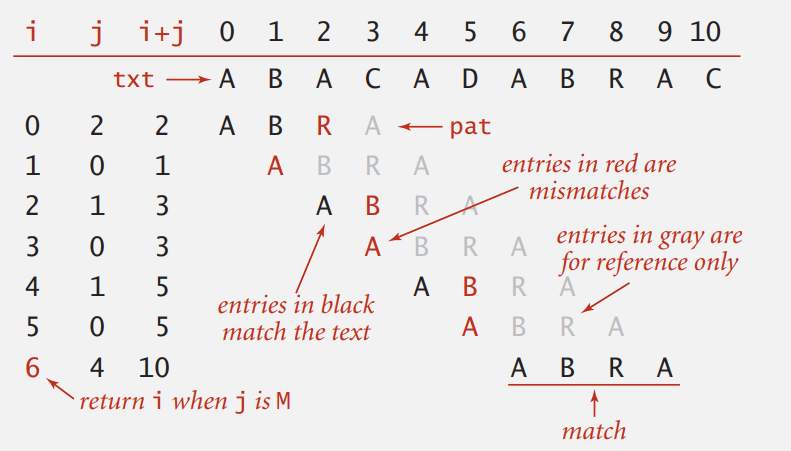
就暴力地两个循环,查找文本的每个位置,最坏情况下需要近似 (MN) 次字符比较。

稍微贴下代码:
public static int search(String pat, String txt) {
int M = pat.length();
int N = txt.length();
for (int i = 0; i <= N - M; i++) {
int j;
for (j = 0; j < M; j++)
if (txt.charAt(i + j) != pat.charAt(j))
break;
if (j == M) return i; // index in txt where pattern starts
return N; // not found
}
}
暴力算法有可能会跑的很慢,而且还存在一个回退(backup)问题:

这是暴力算法的另一个实现代码(显示回退):
public static int search(String pat, String txt) {
int i, N = txt.length();
int j, M = pat.length();
for (i = 0, j = 0; i < N && j < M; i++) {
if (txt.charAt(i) == pat.charAt(j)) j++;
else {
i -= j; // explicit backup
j = 0;
}
if (j == M) return i - M;
else return N; // not found
}
}
所以暴力算法并不是总能满足我们的需求,我们希望有线性时间级别的性能保证,希望避免在文本流中回退。
Knuth-Morris-Pratt
KMP 算法一下子解决了上面两个问题,既不用回退,最多也只要访问 N 次字符,于是我们先来了解下 DFA。
Deterministic Finite State Automaton
确定型有穷(状态)自动机(DFA),是一个抽象的字符串查找机器。
-
状态数目是有穷的(包括初始状态和终结状态)。
-
每个状态对每个字符有且仅有一个转移。
-
转移到终结状态则接受这个字符串,即含有我们寻找的子串(模式)。
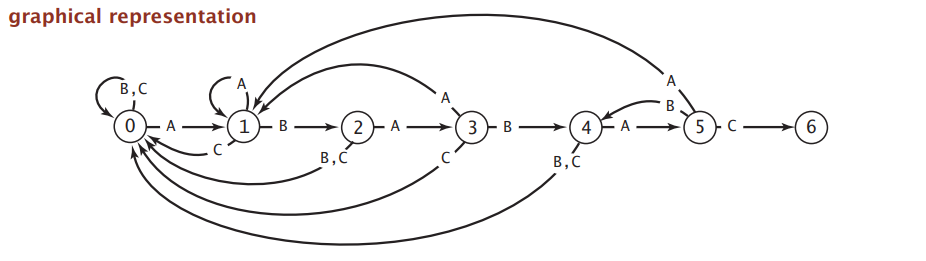
比如说,现在我们在一个由字母 A, B 和 C 组成的文本中寻找子串:ABABAC,DFA 长这样:
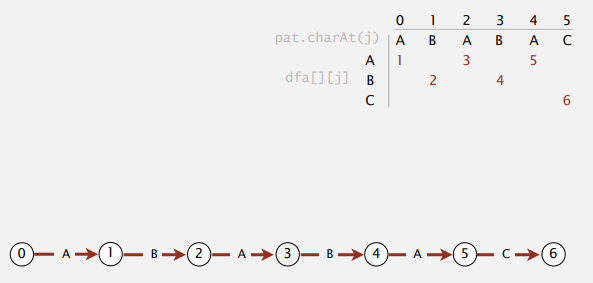
具体实现时用二维数组表示就好:
j 0 1 2 3 4 5
--------------------------
pat.charAt(j) A B A B A C if in state j reading char c:
|A 1 1 3 1 5 1 if j is 6 halt and accept
dfa[][j]|B 0 2 0 4 0 4 else move to state dfa[c][j]
|C 0 0 0 0 0 6
其中 dfa[i][j] 表示状态 j 遇到字符 i 会转移到下一个状态,并不包括终结状态。
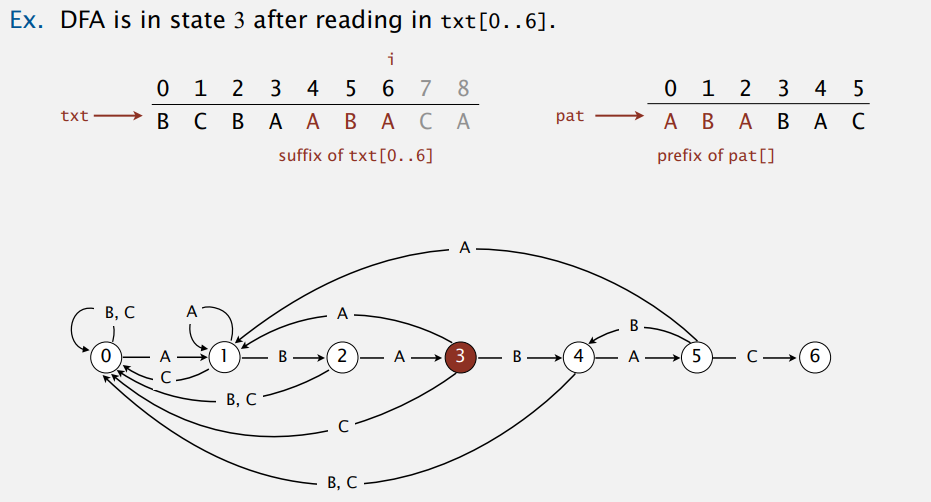
现在查找子串就很简单啦,一开始在初始状态,文本流读到哪个字符就往哪条路走,要是走到了终结状态,也就表示找到了子串。像我们这样构造的 DFA,走到状态几,就说明已经匹配了多少个字符其实,所以走到终结状态就表示全部匹配。例子,状态三:
KMP Substring Search: Java Implementation
public int search(String txt) {
int i, j, N = txt.length();
for (i = 0, j = 0; i < N && j < M; i++)
j = dfa[txt.chaAt(i)][j]; // no backup
if (j == M) return i - M;
else return N; // not found
}
在二维数组 dfa 的指导下,查找子串的代码很简单,即没有回退,最多也只要 N 次字符访问。于是乎,关键就在于如何从要查找的子串构造相应的 dfa[][] 啦。
Construct DFA
-
Match Transition
匹配时的转移很好办,直接到下一个状态即可。
-
Mismatch Transition
关键在不匹配时该如何转移。
假设在状态 j 时读到的下一个字符 c 不等于要找的子串的第 j + 1 个字符(pat.charAt(j),从 0 标号),那么这个时候,我们从文本流中最近读出的 j - 1 个字符即为 pat[1..j - 1] + c,就是暴力算法要重新扫描的部分。
当前首字母到状态 j 出现了不匹配,按暴力算法该丢弃它从下一个字母再开始,即 pat[1],再一路重新扫描到 c。所以,现在状态 j 遇到 c 该怎么转移,实际上和字符串 pat[1.. j - 1] + c 在 DFA 中所到状态碰到 c 的转移目标一样才对。于是我们这么计算 dfa[c][j]:在 DFA 上模拟 pat[1.. j - 1],然后直接取字符 c 的转移。
举个例子来看,如何计算状态 5 碰到字符 A 和 B 的转移:

这样,乍一看需要 j 步来模拟暴力算法中回退部分字符输入到 DFA,从而找到不匹配时的重启状态(像上图的状态 3)。但其实,我们可以花很小的成本来维护重启状态 X,不匹配时就能一下知道该转移到哪。其实也就是从 pat[1] 开始匹配而已,具体可以看下面代码。
Construcing DFA For KMP: Java Implementation
public KMP(String pat) {
this.pat = pat;
M = pat.length();
dfa = new int[R][M];
dfa[pat.charAt(0)][0] = 1; // 初始状态只要这一个转移,其它还是自己(0)
// 构造 dfa[][1..M - 1] 没有终结状态的转移
for (int X = 0, j = 1; j < M; j++) {
for (int c = 0; c < R; c++)
dfa[c][j] = dfa[c][X]; // copy mismatch cases
// 匹配时,状态和重启状态没关系,以当前状态为主,直接下一状态
dfa[pat.charAt(j)][j] = j + 1; // set match case
// 从 pat[1] 开始匹配
X = dfa[pat.charAt(j)][X]; // update restart state
}
}
Boyer-Moore
Boyer-Moore 算法采用启发式(heuritic)的方法处理不匹配的字符,从右向左扫描模式字符串(长度为 M)并将它和文本匹配,不匹配的时候最多可以跳过 M 个文本中的字符,在实际应用中近似能达到 (N/M) 级别。例子:

第一次文本中的 N 和模式中的 E 不匹配,因为模式串中含有 N,所以将模式中最右边的 N 和其对齐,模式一下就向右移动了 5 位。第二次不匹配时,因为模式串中没有 S,更是直接将模式串移动了 6 位(即 M 位)。最终找到匹配的位置总共也只比较了四次,还有另外六次用来验证匹配。
因为实际中模式串经常只包含字母表中一些字符,在文本中查找的时候经常碰到模式串中没有的字符,所以几乎全部都是这种跳过 M 位的,故近似有 (N/M) 级别。
于是关键就在于:移动几位,具体可以分为以下三种情况:
-
不匹配字符不在模式串中。
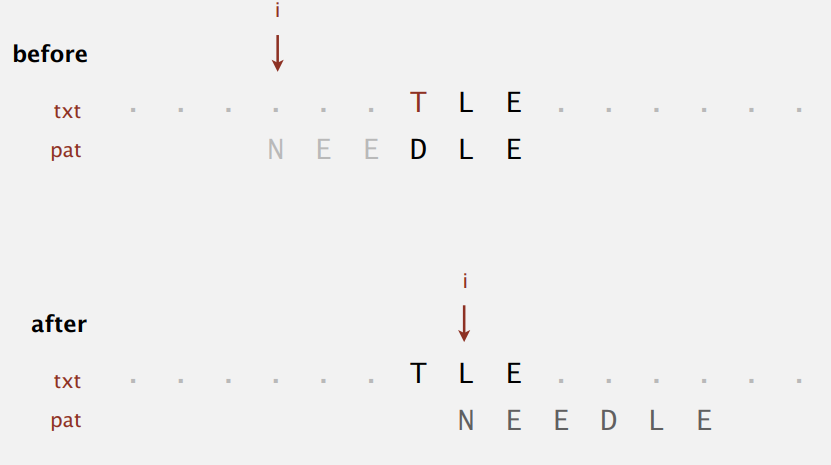
这是最简单的情况,直接移动 M 位。
-
不匹配字符在模式串中,情形一。
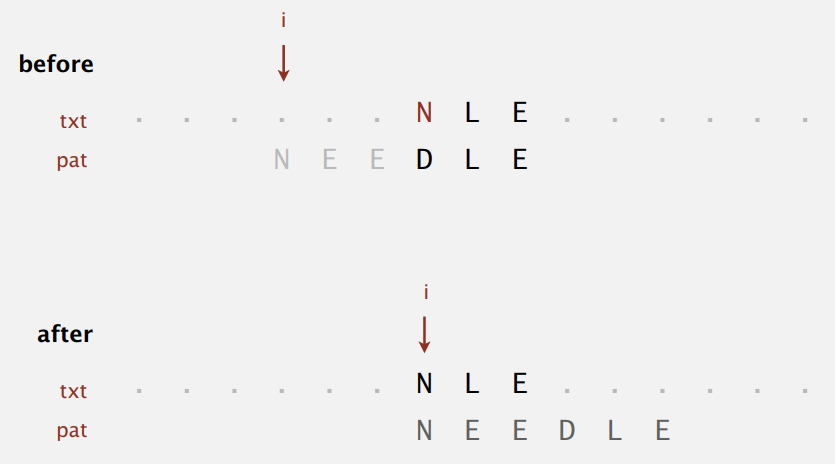
将模式串中最右边的该字符和文本中的对齐。
-
不匹配字符在模式串中,情形二。

这时要是按上面和最右边的对齐,模式串会往左边移动发生回退,移动位数是负数。所以这时没办法跳过很多字符,只能老实地右移一位。
具体的实现时,对模式串进行下预处理,维护一个数组 right[R] 来指导跳过几位就好。
rigth = new int[R];
for (int c = 0; c < R; c++)
right[c] = -1; // 模式串中没有该字符则记为 -1
for (int j = 0; j < M; j++)
right[pat.charAt(j)] = j;
Boyer-Moore: Java Implementation
public int search(String txt) {
int N = txt.length();
int M = pat.length();
int skip;
for (int i = 0; i <= N - M; i += skip) {
skip = 0;
for (int j = M - 1; j >= 0; j--) {
if (pat.charAt(j) != txt.charAt(i + j)) {
// in case other term is nonpositive
skip = Math.max(1, j - right[txt.charAt(i + j)]);
}
}
if (skip == 0) return i; // match
}
return N;
}
最坏的情况下,Boyer-Moore 算法会退化到近似 (MN) 的级别,就是都是最后一种情形,每次只能移动一位。

完整的 Boyer-Moore 算法和 KMP 算法类似有个记录不匹配时的重启位置的数组,能给最坏情况提供线性级别的性能保证,跳过的位数也可能不止 M 位。不过对一般的应用程序,启发式的处理不匹配字符已经足够了,所以不展开,据说就是从模式串右边开始构造 DFA。
Rabin-Karp
Rabin-Karp 指纹字符串查找算法基于模数(modular)散列,直接上图:

我们用的散列函数如下:
(x_{i} = c_{i}R^{M - 1} + c_{i + 1}R^{M - 2} + ... + c_{i + M - 1}R^{0}) (mod Q)
(c_{i}) 表示第 i 位的字符,Q 就是一个很大的素数(也要注意不要溢出)。然后再用 Horner 方法(霍尔法则计算 n 次多项式)在线性时间内计算出来:
// Compute hash for M-digit key
private long hash(String key, int M) {
long h = 0;
for (int j = 0; j < M; j++)
h = (R * h + key.charAt(j)) % Q;
return h;
}
上面的方法模式串和文本都能用,但每次计算文本的子串的散列需要访问 M 个字符,那和暴力算法不都是近似 (MN) 级别。Rabin-Karp 算法的关键就在于它能够在线性时间内算出文本子串的散列值,只要稍微预处理一下。
考虑下如何在已知 (x_{i}) 的情况下高效地算出 (x_{i + 1}),写出式子:
(x_{i} = c_{i}R^{M - 1} + c_{i + 1}R^{M - 2} + ... + c_{i + M - 1}R^{0})
(x_{i + 1} = c_{i + 1}R^{M - 1} + c_{i + 2}R^{M - 2} + ... + c_{i + M}R^{0})
不难推出:
(x_{i + 1} = (x_{i} - t_{i}R^{M - 1}) R + t_{i + M})
可以先把 (R^{M - 1}) 算好,例子:

Rabin-Krap: Java Implementation
public class RabinKrap {
private long patHash; // pattern hash value
private int M; // pattern length
private long Q; // modulus
private int R; // radix
private long RM; // R^(M-1) % Q
public RabinKrap(String pat) {
R = 256;
M = pat.length();
patHash = hash(pat, M);
// a large prime
// but avoid overflow
Q = longRandomPrime();
RM = 1;
for (int i = 1; i <= M -1; i++)
RM = (R * RM) % Q;
}
public int search(String txt) {
int N = txt.length();
int txtHash = hash(txt, M);
if (patHash == txtHash) return 0;
for (int i = M; i < N; i++) {
txtHash = (txtHash + Q - RM * txt.charAt(i - M) % Q) % Q;
txtHash = (txtHash * R + txt.charAt(i)) % Q;
if (patHash == txtHash) return i - M + 1; // Monte Carlo version
}
return N; // not found
}
}
蒙特卡洛版本在散列匹配时直接返回,因为散列表的规模 Q 很大,冲突概率很小,这样可以保证运行时间。另有拉斯维加斯(Las Vegas)版本散列值匹配后还会回退比较字符,以此来保证正确性,但可能会很慢。
Rabin-Karp 算法的优点是容易拓展,像是拓展到查找多模式,查找二维模式等,缺点是算术运算会比其它算法的字符比较慢等。