来源:
部分来自wiki:https://en.wikipedia.org/wiki/Coherence_(signal_processing);
部分来自网络其它内容。
The coherence (sometimes called magnitude-squared coherence) between two signals x(t) and y(t) is a real-valued function that is defined as:
where Gxy(f) is the cross-spectral density between x and y, and Gxx(f) and Gyy(f) the autospectral density of x and y respectively. The magnitude of the spectral density is denoted as |G|. Given the restrictions noted above (ergodicity, linearity) the coherence function estimates the extent to which y(t) may be predicted from x(t) by an optimum linear least squares function (最优线性最小二乘函数).
Values of coherence will always satisfy 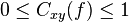 .
.
For an ideal constant parameter linear system with a single input x(t) and single output y(t), the coherence will be equal to one. If Cxy is less than one but greater than zero it is an indication that either: noise is entering the measurements, that the assumed function relating x(t) and y(t) is not linear, or that y(t) is producing output due to input x(t) as well as other inputs. If the coherence is equal to zero, it is an indication that x(t) and y(t) are completely unrelated, given the constraints mentioned above.
The coherence of a linear system therefore represents the fractional part of the output signal power that is produced by the input at that frequency. We can also view the quantity  as an estimate of the fractional power of the output that is not contributed by the input at a particular frequency. This leads naturally to definition of the coherent output spectrum:
as an estimate of the fractional power of the output that is not contributed by the input at a particular frequency. This leads naturally to definition of the coherent output spectrum:
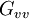 provides a spectral quantification of the output power that is uncorrelated with noise or other inputs.
provides a spectral quantification of the output power that is uncorrelated with noise or other inputs.
一些补充知识:






