论文题目:YOLOv4: Optimal Speed and Accuracy of Object Detection
文献地址:https://arxiv.org/pdf/2004.10934.pdf
源码地址:https://github.com/AlexeyAB/darknet

YOLOv4中谈及了许多近年来提出的激活函数,包括ReLU,LReLU,PReLU,ReLU6,ELU,SELU,Swish,hard-Swish和Mish。 本文总结这些深度学习的损失函数。
01 sigmoid与tanh
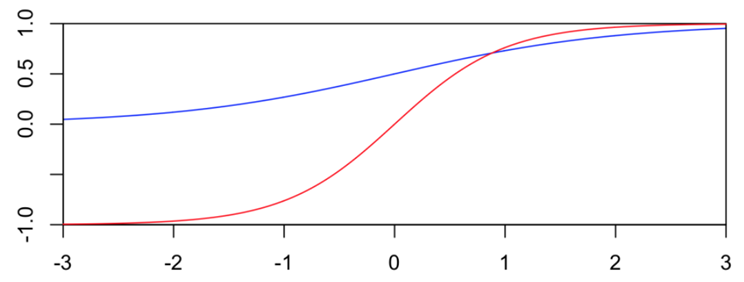
Sigmoid和tanh是有着优美的S型曲线的数学函数。在逻辑回归、人工网络中有着广泛的应用。
从数学上来看,非线性的Sigmoid函数对中央区的信号增益较大,对两侧区的信号增益小,在信号的特征空间映射上,有很好的效果。
从神经科学上来看,中央区酷似神经元的兴奋态,两侧区酷似神经元的抑制态,因而在神经网络学习方面,可以将重点特征推向中央区,将非重点特征推向两侧区。
无论是哪种解释,看起来都比早期的线性激活函数(y=x),阶跃激活函数(-1/1,0/1)高明了不少。
sigmoid
sigmoid将输入映射到[0, 1]之间。数学形式为:
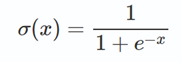
函数图像:
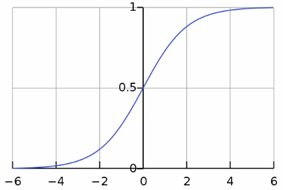
缺点:
-
存在饱和现象,造成梯度消失。
- 表达能力的极限在-6~6之间;
- 在-3~3之间会有比较好的效果;
- 不是关于原点中心对称的。
tensorflow调用:
1 tf.nn.sigmoid(x, name=None)
tanh
tanh将输入映射到[-1, 1]之间,输出是原点中心对称的。但函数值变化敏感,同样存在饱和问题。tanh实际上是一个放大的sigmoid函数,可以表示为2sigmoid(2x)-1,也可以表示为:
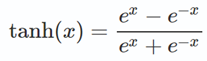
函数图像:
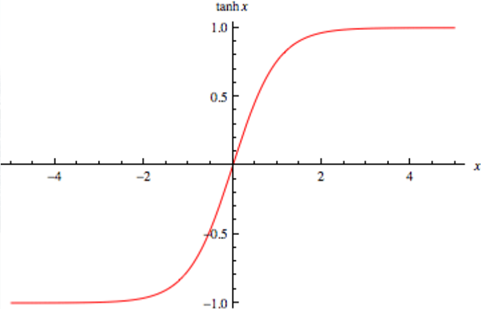
tensorflow调用
1 tf.nn.tanh(x, name=None)
一般而言,当特征相差明显时,使用tanh效果会很好;当特征相差不是特别大,sigmoid函数效果会更好一些。
02 ReLU系列
近年来ReLU非常流行,并且包含很多变体:ReLU,ReLU6,LReLU,PReLU
ReLU
![]()
函数图像:
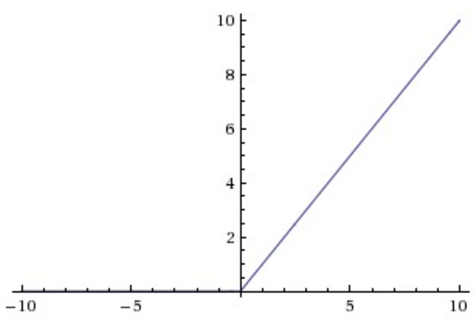
优点:
- 相较于 sigmoid 和 tanh 函数, ReLU 对于 SGD 的收敛有巨大的加速作用。并且,有文献指出有6倍之多。
- 计算量小,没有指数的运算,对硬件友好;
- 有很好的稀疏性。即,将数据转化为只有最大数值,其他都为0。
缺点:
- 造成神经元"dead"[对于输入为负值,全部为0]
- 可能会造成梯度爆炸,输出没有上限。
tensorflow调用:
1 tf.nn.relu(features, name=None)
在实际使用时,会对relu增加上界的设定,即ReLU6:
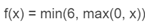
tensorflow调用:
1 tf.nn.relu6(features, name=None)
softplus函数与ReLU函数接近,但比较平滑, 同ReLU一样是单边抑制,有宽广的接受域(0,+inf), 但是由于指数运算/对数运算计算量大的原因,而不太被人使用.
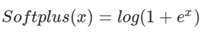
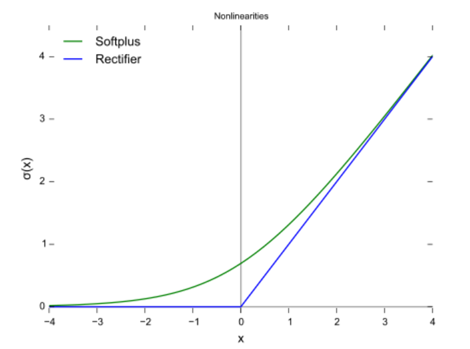
2003年Lennie等人估测大脑同时被激活的神经元只有1~4%,进一步表明神经元工作的稀疏性。
从信号方面来看,即神经元同时只对输入信号的少部分选择性响应,大量信号被刻意的屏蔽了,这样可以提高学习的精度,更好更快地提取稀疏特征。
Leaky ReLU(LReLU) && Parametric ReLU(PReLU)
针对ReLU会造成很多神经元dead的问题的改进。可以统一表达为下式:
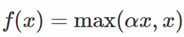
不同的是Leaky ReLU的α是固定的,而Parametric ReLU的α不是固定的,是通过训练得到的。
LReLU:
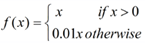
ReLU 中当 x<0 时,函数值为 0 。而 Leaky ReLU 则是给出一个很小的负数梯度值,比如 0.01 。
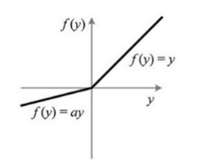
tensorflow调用:
1 tf.nn.leaky_relu(features, alpha=0.2, name=None)
PReLU:
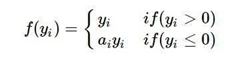
函数图像如下:
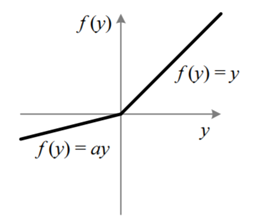
与LReLU不同的是,PReLU中的α不是固定的,而是可以学习的。解决了超参数α难设定的问题。
也就是说,PReLU为带参数的ReLU。如果ai=0,那么PReLU退化为ReLU;如果ai是一个很小的固定值(如ai=0.01),则PReLU退化为Leaky ReLU(LReLU)。 有实验证明,与ReLU相比,LReLU对最终的结果几乎没什么影响。

ReLU family:
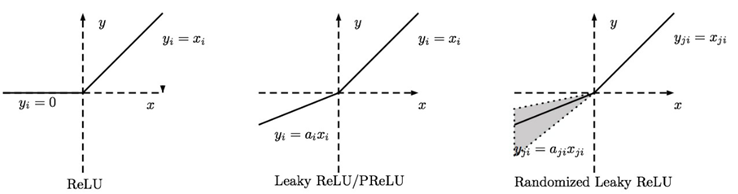
(Randomized Leaky ReLU的α是由一个高斯分布中随机产生的)
03 ELU系列
ELU
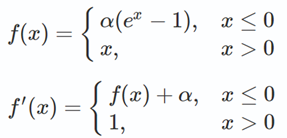
图像如下:
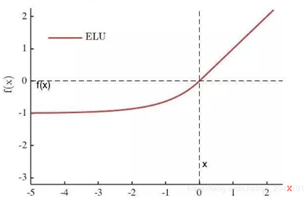
从表达式与图像上看:
- ELU融合了sigmoid和ReLU,左侧具有软饱和性,右侧无饱和性;
- ELU的输出均值接近于0,收敛速度更快
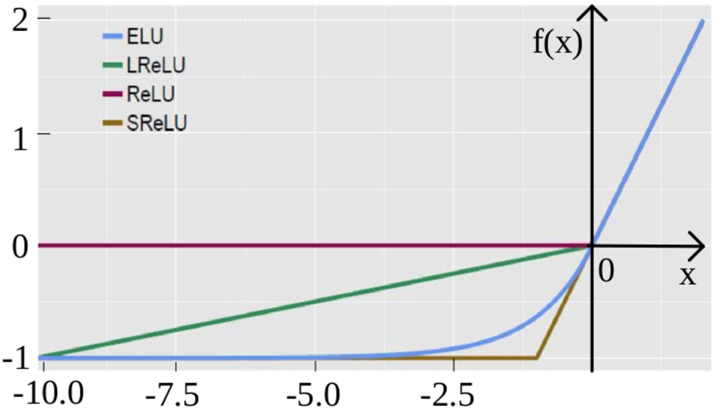
SELU

这是一个在一篇102页paper发表出来的激活函数,全篇90多页的附录,书写了公式证明... 总结其实就是下式,直观来看,就是给ELU的表达式乘以了λ。即SELU(x)=λ·ELU(x)(有兴趣可以一观https://arxiv.org/pdf/1706.02515.pdf)
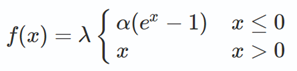
其中,

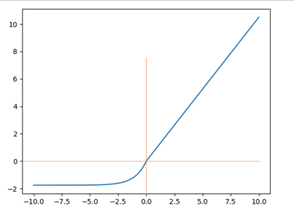
tensorflow调用
1 tf.nn.selu(features, name=None)
04 Swish && hard-Swish
swish
谷歌大脑在selu出了不久就提出了swish激活函数方法,秒杀所有激活函数。
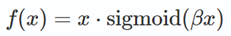
其中σ表示sigmoid函数。
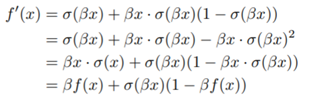
β是个常数或可训练的参数。Swish 具备无上界有下界、平滑、非单调的特性。
Swish 在深层模型上的效果优于 ReLU。例如,仅仅使用 Swish 单元替换 ReLU 就能把 NASNetA 在 ImageNet 上的 top-1 分类准确率提高 0.9%,Inception-ResNet-v 的分类准确率提高 0.6%。

tensorflow调用
1 tf.nn.swish(features, name=None)
或者可以手动编写:
1 x * tf.sigmoid(beta * x)
Hard-swish
Hard-Swish是在MobileNetv3中提出的,是针对Swish函数的sigmoid操作对硬件不够友好的问题做的改进。使用ReLU6的改善

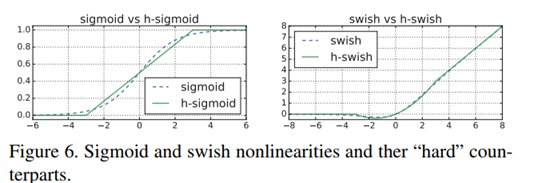
05 Mish
![]()
https://github.com/digantamisra98/Mish
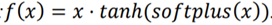
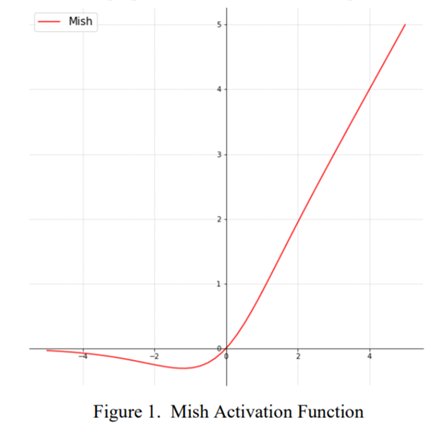
从函数表达式上来看,Mish的计算量着实不小;
从上图中看,Mish的图像略微古怪,居然不是单调的;
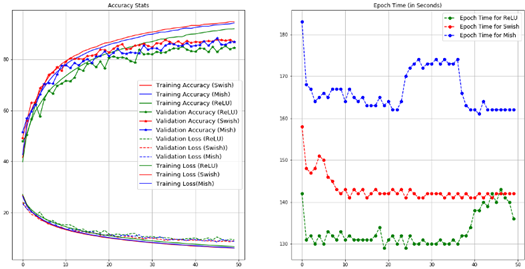
但从下图来看,效果着实不错。
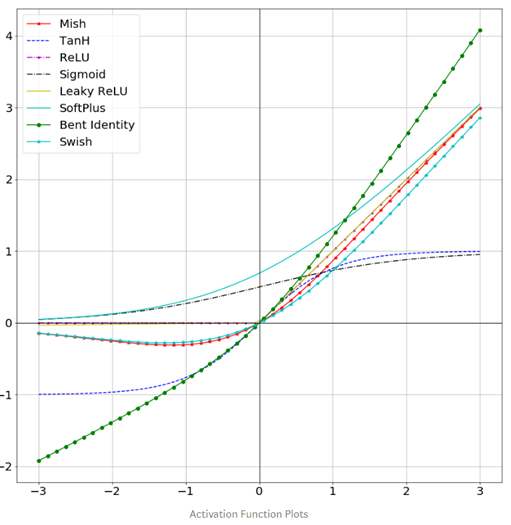
激活函数大汇总
参考:
(1)https://www.cnblogs.com/makefile/p/activation-function.html
(2)https://www.cnblogs.com/neopenx/p/4453161.html
(3)https://blog.csdn.net/u011984148/article/details/101444274