无向图
无向图由顶点和边组成。边用于连接两个顶点。
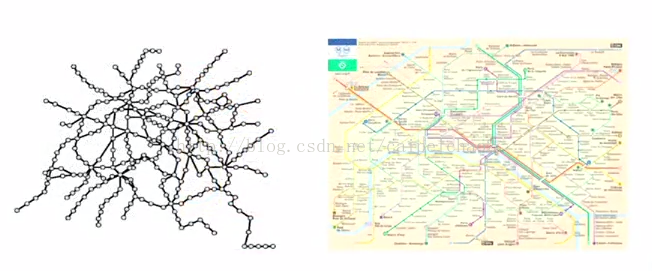
以下这张地图就是无向图的一个样例。
OPTEproject
OPTEproject的目标就是绘制整个互联网的样子。
下图是2010年的互联网。互联网也是无向图的一个样例。这张图是用LGL软件进行绘制的。有兴趣的同学可以研究一下:http://www.opte.org/
术语
在图论中,有些术语是必需要知道的,不然没办法学习。
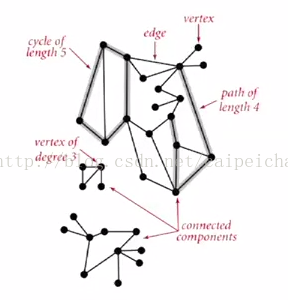
顶点:图中最主要的元素
边:连接两个顶点的线就是边
路径:由一个顶点到还有一个顶点所经过的边
环:从一个顶点出发,经过一些边。最后到达原先的顶点。那么这个路径就是环。
连接部件:全部相互连接的顶点和边就是一个连接部件。一个图中可能会有多个连接部件。以下这张图中就有三个连接部件。
图论问题
和图论有关的问题在这里罗列一下。
最短路径:从一个顶点到还有一个顶点的最短路径是什么?
路径问题:从一个顶点能不能到达另外一个顶点呢?
是否有环:一张图中是否含有环?
欧拉旅行问题:从一个顶点出发。每条边仅仅能经过一次。要求经过全部的边,请问该怎么走?
哈密尔顿旅行问题:从一个顶点出发,每一个顶点仅仅能经过一次。要求经过全部的顶点。请问该怎么走?
连接问题:有没有办法可以连接全部的顶点呢?
MST:最小生成树。
怎样用最短的边连接全部的顶点?
双向连接:是否存在一个关键的顶点。使得它的移除会造成图断裂成两个部件?
是否平面:是否能让图在一个平面中表示,并且全部的边互不交叉?
图的同构:两张图是否等价?
下图是哥尼斯堡七桥问题。
从不论什么一个岛屿開始,每一个桥仅仅能走一次,要求经过全部的桥,该怎么走?当时哥尼斯堡无法求解这个问题,并且他也不是著名的人物,于是怀着渺茫的希望请教著名数学家欧拉,给他写了一封信。万万没想到非常快就得到了欧拉的回应。欧拉不但攻克了这个问题。并且还创立了一套图论。