计算机辅助解题

1. 复杂的组合问题

• 2 个人各自拿着 A~K 的 13 张牌，每次按顺序，一人出一张，13 轮结束，每次出的都不是相同数字的概率，

13 张牌，情况较为复杂，我们首先考虑 3 张牌的情况，已知自己是 1,2,3，则要求对方在各个位置上都与自己不同，只有两种选择，3,1,2 和 2,3,1。

#include <algorithm>            // next_permutation(...)

// 13 张牌的情况较多
int arr[] = { 1, 2, 3, 4, 5, 6, 7, 8};
int tmp[] = { 1, 2, 3, 4, 5, 6, 7, 8};
int cnt = 0;

do {

    for (int i = 0; i < 8; ++i) {
        if (arr[i] == tmp[i]) {
            ++cnt;
            break;
        }
    }

} while (next_permutation(tmp, tmp + 8));

cout << cnt << endl;

2. 数三角形的个数

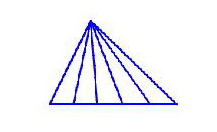
我们不采用做奥数题的思路，而是编程求解：

matrix = [
    ['A', 'A', 'A', 'A', 'A', 'A'],
    ['B', 'C', 'D', 'E', 'F', 'G']
]

def pair(lis):
    n = len(lis)
    for i in range(n):
        for j in range(i+1, n):
            yield lis[i], lis[j]

triangles = []
for line_a, line_b in pair(matrix):
    for i, j in pair(range(len(line_a))):
        shape = [line_a[i], line_a[j], line_b[i], line_b[j]]
        shape.sort()
        for node_a, node_b in pair(shape):
            if node_a == node_b and shape not in triangles:
                triangles.append(shape)
print(triangles)
print(len(triangles))
                # 可得 15 

再考虑如下的较为复杂的图形：

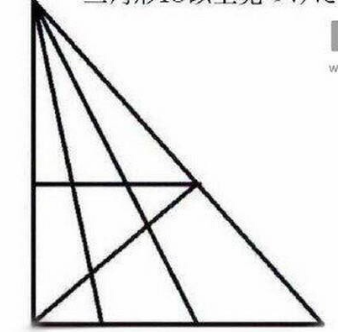
此时，只需修改上述代码的：

matrix = [
    ['A', 'A', 'A', 'A'],
    ['B', 'C', 'D', 'E'],
    ['H', 'G', 'F', 'E'],                    # 右上斜向左下的线段
    ['H', 'I', 'J', 'K']
]