1.贝叶斯原理:
它是建立在主观判断的基础上:在我们不了解所有客观事实的情况下,同样可以先估计一个值,然后根据实际结果不断进行修正。
先验概率:通过经验来判断事情发生的概率
后验概率:发生结果之后,推测原因的概率。
条件概率:事件 A 在另外一个事件 B 已经发生条件下的发生概率,表示为 P(A|B),读作“在 B 发生的条件下 A 发生的概率”。
似然函数(likelihood function):
你可以把概率模型的训练过程理解为求参数估计的过程。举个例子,如果一个硬币在 10 次抛落中正面均朝上。那么你肯定在想,
这个硬币是均匀的可能性是多少?这里硬币均匀就是个参数,似然函数就是用来衡量这个模型的参数。似然在这里就是可能性的意思,
它是关于统计参数的函数。
贝叶斯公式:
假设有一种病叫做“贝叶死”,它的发病率是万分之一,即 10000 人中会有 1 个人得病。现有一种测试可以检验一个人是否得病的准确率
是 99.9%,它的误报率是 0.1%
A:表示事件“测出为阳性”
B1:表示“患有贝叶死”
B2:表示“没有患贝叶死”
(1) 患有贝叶死的情况下,测出为阳性的概率为P(A|B1) = 99.9%
(2) 没有患有贝叶死,测出为阳性的概率为P(A|B2) = 0.1%
(3) 患有贝叶死的概率为P(B1) = 0.01%
(4) 没有患贝叶死的概率为P(B2) = 99.99%
==>检测出来为阳性,而且是贝叶死的概率P(B1,A) = p(B1)*p(A|B1) = 0.01%*99.9% = 0.00999%
==>检测出来为阳性,而且不是贝叶死的概率P(B2,A) = p(B2)*p(A|B2) = 99.99%*0.1% = 0.09999%
===>检查为阳性,患有贝叶死的概率P(B1|A) = 0.01% / (0.01% + 0.1%) = 9%
===>检查为阳性,但没有患有贝叶死的概率P(B2|A) = 0.1% / (0.01% + 0.1%) = 90.9%
我们把(0.01% + 0.1%)均出现在计算P(B1|A) 和 P(B2|A) 时的分母位置上的叫做论据因子,也相当于一个权值因子!
基于刚刚计算P(B1|A) 和 P(B2|A)的方法,我们总结出贝叶斯公式为:
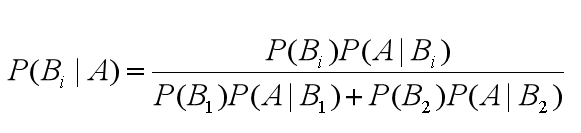
由此,我们可以得出通用的贝叶斯公式:

2.朴素贝叶斯:
它是一种简单但极为强大的预测建模算法。之所以称为朴素贝叶斯,是因为它假设每个输入变量是独立的。这是一个强硬的假设,
实际情况并不一定,但是这项技术对于绝大部分的复杂问题仍然非常有效。
朴素贝叶斯模型由两种类型的概率组成:
(1) 每个类别的概率P(Cj);
(2) 每个属性的条件概率P(Ai|Cj)。
什么是类别概率和条件概率?
假设我有 7 个棋子,其中 3 个是白色的,4 个是黑色的。
那么棋子是白色的概率就是 3/7,黑色的概率就是 4/7,这个就是类别概率。
假设我把这 7 个棋子放到了两个盒子里,其中盒子 A 里面有 2 个白棋,2 个黑棋;盒子 B 里面有 1 个白棋,2 个黑棋。
那么在盒子 A 中抓到白棋的概率就是 1/2,抓到黑棋的概率也是 1/2,这个就是条件概率,也就是在某个条件(比如在盒子 A 中)
下的概率。
在朴素贝叶斯中,我们要统计的是属性的条件概率,也就是假设取出来的是白色的棋子,那么它属于盒子 A 的概率是 2/3。
3.贝叶斯原理、贝叶斯分类和朴素贝叶斯三者之间的区别?
贝叶斯原理是最大的概念,它解决了概率论中“逆向概率”的问题,在这个理论基础上,人们设计出了贝叶斯分类器,
朴素贝叶斯分类是贝叶斯分类器中的一种,也是最简单,最常用的分类器。朴素贝叶斯之所以朴素是因为它假设属性是相互独立的,
因此对实际情况有所约束,如果属性之间存在关联,分类准确率会降低。不过好在对于大部分情况下,朴素贝叶斯的分类效果都不错。
