CodeForces 605 E. Intergalaxy Trips

E. Intergalaxy Trips

time limit per test：2 seconds

memory limit per test：256 megabytes

input：standard input

output：standard output

The scientists have recently discovered wormholes — objects in space that allow to travel very long distances between galaxies and star systems.

The scientists know that there are n galaxies within reach. You are in the galaxy number 1 and you need to get to the galaxy number n. To get from galaxy i to galaxy j, you need to fly onto a wormhole (i, j) and in exactly one galaxy day you will find yourself in galaxy j.

Unfortunately, the required wormhole is not always available. Every galaxy day they disappear and appear at random. However, the state of wormholes does not change within one galaxy day. A wormhole from galaxy i to galaxy j exists during each galaxy day taken separately with probability pij. You can always find out what wormholes exist at the given moment. At each moment you can either travel to another galaxy through one of wormholes that exist at this moment or you can simply wait for one galaxy day to see which wormholes will lead from your current position at the next day.

Your task is to find the expected value of time needed to travel from galaxy 1 to galaxy n, if you act in the optimal way. It is guaranteed that this expected value exists.

Input

The first line of the input contains a single integer n (1 ≤ n ≤ 1000) — the number of galaxies within reach.

Then follows a matrix of n rows and n columns. Each element pij represents the probability that there is a wormhole from galaxy i to galaxy j. All the probabilities are given in percents and are integers. It is guaranteed that all the elements on the main diagonal are equal to 100.

Output

Print a single real value — the expected value of the time needed to travel from galaxy 1 to galaxy n if one acts in an optimal way. Your answer will be considered correct if its absolute or relative error does not exceed 10 - 6.

Namely: let's assume that your answer is a, and the answer of the jury is b. The checker program will consider your answer correct, if .

Examples

input

3
100 50 50
0 100 80
0 0 100

output

1.750000000000000

input

2
100 30
40 100

output

3.333333333333333

Note

In the second sample the wormhole from galaxy 1 to galaxy 2 appears every day with probability equal to 0.3. The expected value of days one needs to wait before this event occurs is .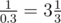

题意：

给出一张$n$个点$n^{2}$条边的有向图，每条边每天的出现概率为$p[i][j]$，求从$1$到$n$的期望天数...

分析：

首先我们考虑两个点的情况，也就是第二个样例，从$1$到$2$的边的出现概率为$0.3$，所以我们此时求的期望天数就是期望第几天会出现这条边：$ans=sum _{i=0}^{+∞}0.7^{i}$，收敛一下就是$frac {1}{0.3}$...

然后我们再考虑多个点的情况，如果我们要从$i$走到$j$，必须满足的是走到$j$之后的结果要比$i$优，否则就不走...所以我们是每次选取一个最优的点去更新其他的点，这就是一个$dijkstra$的过程，更新的方式就是$f[i]=frac {(p[i][j_{1}]*f[j_{1}]+(1-p[i][j_{1}])*p[i][j_{2}]*f[j_{2}]+……+1)}{1-(1-p[i][j_{1}])(1-p[i][j_{2}])……}$...

代码：

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio> 
#include<queue>
//by NeighThorn
using namespace std;

const int maxn=1000+5;

int n,vis[maxn];

double f[maxn],a[maxn],b[maxn],p[maxn][maxn];

struct M{
	
	int x;
	double y;
	
	friend bool operator < (M a,M b){
		return a.y>b.y;
	}
	
	M(int a=0,double b=0.0){
		x=a;y=b;
	}
	
};

priority_queue<M> q;

signed main(void){
	scanf("%d",&n);
	for(int i=1,x;i<=n;i++)
		for(int j=1;j<=n;j++)
			scanf("%d",&x),p[i][j]=x/100.0;
	for(int i=1;i<=n;i++)
		a[i]=b[i]=1.0,f[i]=1e30;
	f[n]=0;q.push(M(n,0));
	while(!q.empty()){
		int top=q.top().x;q.pop();
		if(vis[top])
			continue;
		vis[top]=1;
		for(int i=1;i<=n;i++)
			if(p[i][top]>0&&!vis[i]){
				a[i]+=b[i]*p[i][top]*f[top];
				b[i]*=1.0-p[i][top];
				f[i]=a[i]/(1.0-b[i]);
				q.push(M(i,f[i]));
			}
	}
	printf("%.15f
",f[1]);
	return 0;
}

　　

---

By NeighThorn