A. Puzzle Pieces
(Description:)
是否可以拼成 (n imes m) 的矩形的拼图?
(Solve:)
两个拼图的连接处需要一个凹槽,那么计算一下 (n imes m) 的 矩形拼图需要几个凹槽,再跟总凹槽数即 (n imes m) 比较一下即可。
(Code:)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main(){
int t; cin >> t;
while(t --){
ll n, m;
cin >> n >> m;
if(n * m < (n - 1) * m + (m - 1) * n)
puts("NO");
else puts("YES");
}
return 0;
}
B. Card Constructions
(Description:)
你有 (n) 张牌来搭建金字塔,搭建能搭建最高的,问可以搭建几座金字塔?
(Solve:)
预处理出搭建不同高度的金字塔需要的卡牌,然后直接二分即可。
(Code:)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int INF = 1e9;
vector<int> vec;
void init(){
vec.push_back(0);
int a = 2, b = 0;
while(1){
ll t = a + b * 3;
if(t <= INF && t > 0) vec.push_back(t);
else break;
b += a / 2;
a += 2;
}
}
int main(){
init();
int t; cin >> t;
while(t --){
int n;
cin >> n;
int ans = 0;
while(n){
auto it = upper_bound(vec.begin(), vec.end(), n);
it --;
if(it == vec.begin()) break;
n -= *it;
ans ++;
}
cout << ans << endl;
}
return 0;
}
C. Hilbert's Hotel
(Description:)
给你包含 (n)个数的数组 (a),问是否存在 (i + a_{i mod n} = j + a_{j mod n},(i,j in Z))?存在输出 (NO),不存在输出 (YES).
(Solve:)
如果存在,那么 (i + a_{i mod n} = j + a_{j mod n} + kn(k in Z)),显然两边在 (mod n) 的情况下是相等的,所以我们只需要算出 ([0, n-1]) 内的数(因为 (((i+n)+a_{(i+n) mod n}) mod n = (i + a_{i mod n}) mod n)),看是否存在相同的数即可。
(Code:)
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int a[N];
int main(){
map<pair<int, int>, int> m1;
m1[{1, 2}] = 1;
cout << m1.count({1, 2}) << endl;
int t; cin >> t;
while(t --){
int n; cin >> n;
for(int i = 0; i < n; i ++) scanf("%d", &a[i]);
map<int, int> m;
int mark = 0;
for(int i = 0; i < n; i ++){
int t = ((i + a[i]) % n + n) % n;
if(m[t]){
mark = 1;
break;
}
m[t] = 1;
}
if(mark == 1) puts("NO");
else puts("YES");
}
return 0;
}
D. Monopole Magnets
(Description:)
每行,每列至少有一个 (S),如果 (N) 和 (S) 在同行或同列中,并且不在同一格,那么 (N) 可以向 (S) 移动一格。(N) 可以走到所有黑格,并且不能走到白格,求最少的 (N) ?
(Solve:)
显然在一个黑格的连通块之内,只需要一个 (N),每个黑格都放上一个 (S) 就可以走完该连通块的所有黑格,所以我们求出黑格的连通块的个数就是最后的答案。
在此之前,我们要把无解的情况筛掉。易得出合法的条件是:
1.一行和一列的黑格必须是连续的;(不连续 (N) 就会走到之间的白格上)
2.如果存在全为白格的行,那么也必须存在全为白格的列.( (N) 也会走到白格)
(Code:)
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
typedef pair<int, int> PII;
int n, m;
char s[N][N];
int row[N], col[N];
PII X[N], Y[N];
int to[4][2] = {{0, 1}, {-1, 0}, {0, -1}, {1, 0}};
/*
* 1.两个黑格之间不能有白格
* 2.有全为白格得行(列),也必须有列(行)全为白格
*/
bool check(){
// 预处理出每行每列有多少黑格,以及每行每列黑格的起点和终点
memset(row, 0, sizeof row);
memset(col, 0, sizeof col);
for(int i = 1; i <= n; i ++){
int mark = 0;
X[i] = {0, 0};
for(int j = 1; j <= m; j ++){
if(s[i][j] == '#'){
row[i] ++;
if(mark == 0){
X[i] = {j, j};
mark = 1;
}else{
X[i].second = j;
}
}
}
}
for(int j = 1; j <= m; j ++){
int mark = 0;
Y[j] = {0, 0};
for(int i = 1; i <= n; i ++){
if(s[i][j] == '#'){
col[j] ++;
if(mark == 0){
Y[j] = {i, i};
mark = 1;
}else{
Y[j].second = i;
}
}
}
}
int mark1 = 0; // 是否有全为白格的行
for(int i = 1; i <= n; i ++){
if(row[i] == 0) mark1 = 1;
else if(row[i] != X[i].second - X[i].first + 1)
return false;
}
int mark2 = 0; // 是否有全为白格的列
for(int j = 1; j <= m; j ++){
if(col[j] == 0) mark2 = 1;
else if(col[j] != Y[j].second - Y[j].first + 1)
return false;
}
if(mark2 + mark1 == 1) return false;
return true;
}
void dfs(int x, int y){
s[x][y] = '.';
for(int i = 0; i < 4; i ++){
int xx = x + to[i][0];
int yy = y + to[i][1];
if(xx >= 1 && xx <= n && yy >= 1 && yy <= m && s[xx][yy] == '#')
dfs(xx, yy);
}
}
int main(){
cin >> n >> m;
for(int i = 1; i <= n; i ++)
scanf("%s", s[i] + 1);
if(check() == false)
{puts("-1"); return 0; }
int cnt = 0;
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= m; j ++)
if(s[i][j] == '#'){
cnt ++;
dfs(i, j);
}
cout << cnt << endl;
return 0;
}
E. Quantifier Question
(Description:)
长为 (n) 的数组 (x),给出 (m) 对 (x_i x_j) 的关系,意为 (x_i < x_j),每个 (x_i) 都有一个限定符号 (Q_i)( (Q_i in (exists, forall)) ),要求满足:
求 (forall) 最多可以就几个,并输出对应的方案。如果没有方案可以满足,就输出 (-1) .
(Solve:)
显然由于小于关系具有传递性,所以我们可以把所有关系整合成图。
(x_i < x_j) 就是 (x_i) 到 (x_j) 的一条有向边,根据这个我们可以建出有向图。显然图里存在环的时候是无解的。
理由:有环就代表存在如下关系:(x_i < x_j, x_j < x_k, x_k < x_i),显然是无解的。
接下来考虑怎么填符号。一个很重要的信息是:限定符号是从 (x_1,x_2,...,x_n) 的。例如:(x_1 < x_2),我们给出一种方案:(exists x_1 forall x_2),解读是:存在一个 (x_1) 小于任意一个 (x_2) ,显然是错误的。即先定下了 (x_1) 的值,再去定之后的值。那么我们的 (forall) 符号只有给对于一个连串的关系中下标最小的。那么映射到有向图中,就是如果一个点所有前驱的最小值和所有后继的最小值大于他本身,那么说明他就是最小的,即可以给他 (forall) 。
用拓扑排序可以检查是否有环,并且帮助我们之后找前驱和后继,另外在找前驱的时候要用到的信息是有向边的起点,所以我们还需要反向建图。
(Code:)
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n, m;
// g1 正向图,g2 反向图
vector<int> g1[N], g2[N];
int d[N]; // 每个点的入度
int pre[N], nxt[N]; // 最小前驱,最小后继
char ans[N];
// 求拓扑排序
bool tuopu(vector<int> &vec){
for(int i = 1; i <= n; i ++){
if(d[i] == 0) vec.push_back(i);
}
for(int i = 0; i < vec.size(); i ++){
int u = vec[i];
for(int j = 0; j < g1[u].size(); j ++){
int v = g1[u][j];
d[v] --;
if(d[v] == 0) vec.push_back(v);
}
}
return vec.size() == n;
}
int main(){
cin >> n >> m;
for(int i = 1; i <= m; i ++){
int x, y; scanf("%d%d", &x, &y);
g1[x].push_back(y);
g2[y].push_back(x);
d[y] ++;
}
vector<int> tp; // 拓扑序列
if(tuopu(tp) == false)
{ puts("-1"); return 0; }
for(int i = 1; i <= n; i ++){
pre[i] = nxt[i] = i; // 初始化
}
// 找前驱
for(int i = 0; i < tp.size(); i ++){
int u = tp[i];
for(int j = 0; j < g2[u].size(); j ++){
int v = g2[u][j];
pre[u] = min(pre[u], pre[v]);
}
}
// 找后继
for(int i = tp.size() - 1; i >= 0; i --){
int u = tp[i];
for(int j = 0; j < g1[u].size(); j ++){
int v = g1[u][j];
nxt[u] = min(nxt[u], nxt[v]);
}
}
int cnt = 0;
for(int i = 1; i <= n; i ++){
if(min(nxt[i], pre[i]) == i){
ans[i] = 'A';
cnt ++;
}
else ans[i] = 'E';
}
ans[n + 1] = '�';
cout << cnt << endl;
printf("%s
", ans + 1);
return 0;
}
F. Résumé Review
(Description:)
给定一个长度为 (n) 的数组 (a),再给定 (k)。
满足下列条件:
1. (0 leq b_i leq a_i)
2. (sum_{i = 1}^{n}b_i = k)
使得 (f(b_1,b_2,...,b_n) = sum_{i = 1}^{n}b_i(a_i - b_i^2)) 最大,输出 (b) 数组。
(Solve:)
参考的博文
首先对于任意一个 (i),我们假设 (Delta x = x(a_i - x^2) - (x-1)(a_i - (x-1)^2) = a_i - 3 imes x^2 + 3 imes x - 1)。意为对于 (i) 来说,(b_i) 相差 (1) 的增量。通过观察我们发现他是递减的,并且他只与 (a_i) 有关,由于 (x) 只能是整数,所以是散点图,那么我们将图画出来:
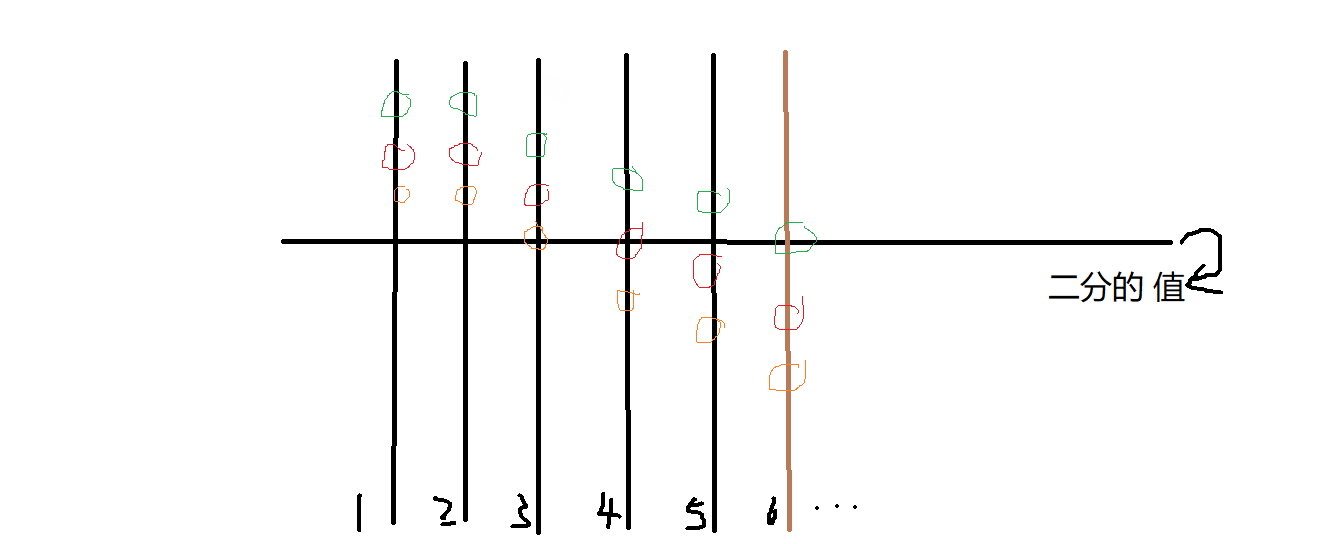
二分图中的横线,理由是我们可以发现点越高,那么他的贡献就会越大,那么只要横线上的点的个数 (geq k) 就是合法的,最后我们再减去多余的点,最后处于横线上的点的贡献是一样的,所以随意减即可。对于任意一个 (i),(Delta x_1 + Delta x_2 + ... + Delta x_{b_i}) 就是他的总贡献。
(Code:)
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
typedef long long ll;
ll n, k;
ll a[N], b[N];
ll cal(ll a, ll x){
return a - 3 * x * x + 3 * x - 1;
}
bool check(ll Y){
ll cnt = 0;
for(int i = 1; i <= n; i ++){
int l = 0, r = a[i];
while(l <= r){
int mid = l + r >> 1;
if(cal(a[i], mid) >= Y) l = mid + 1;
else r = mid - 1;
}
b[i] = l - 1;
cnt += b[i];
}
return cnt >= k;
}
int main(){
cin >> n >> k;
for(int i = 1; i <= n; i ++)
scanf("%lld", &a[i]);
ll l = -4e18, r = 4e18, Y;
while(l <= r){
ll mid = l + r >> 1;
if(check(mid)){
// cout << "mid = " << mid << endl;
Y = mid;
l = mid + 1;
}
else r = mid - 1;
}
check(Y);
ll cnt = 0;
for(int i = 1; i <= n; i ++) cnt += b[i];
cnt -= k;
for(int i = 1; i <= n && cnt; i ++){
if(b[i] && cal(a[i], b[i]) == Y){
cnt --; b[i] --;
}
}
for(int i = 1; i <= n; i ++)
printf("%lld%c", b[i], i == n ? '
' : ' ');
return 0;
}