| 项目 | 内容 |
|---|---|
| 课程班级博客链接 | 班级博客 |
| 这个作业要求链接 | 作业要求 |
| 我的课程学习目标 | 1.掌握软件项目个人开发流程 2.掌握Github发布软件项目的操作方法。 |
| 这个作业在哪些方面帮助我实现学习目标 | 1.认真研读软件开发流程 2.熟悉Github的操作过程 3.分析软件开发任务需求 |
| 项目Github的仓库链接地址 | 我的仓库 |
任务1:阅读教师博客“常用源代码管理工具与开发工具”内容要求,点评班级博客中已提交相关至少3份作业。
任务2:详细阅读《构建之法》第1章、第2章,掌握PSP流程.
- 第1章
“什么是好的软件,一些同学认为,所谓好软件,就是软件没有缺陷(bug),所谓软件工程就是把软件中的bug都消灭的过程。这的确抓住了软件工程的一个要素”
问题:
(1)好的软件除了从用户满意度,可靠性,软件流程的质量,可维护性这样宏观的角度衡量,具体可以用哪些指标衡量?
(2)bug数和软件好坏的关系是怎样的?- 我的看法:
(1)这句话引发了我对如何衡量软件的好坏的思考。也通过百度得知了衡量软件质量的5个最常用的指标:SLOC(源代码行,可以使用Metrics工具来统计);每个代码段/模块/时间段中的bug数;代码覆盖率(单元测试阶段考虑);设计/开发约束(可维护性,可读性);圈复杂度(用来衡量一个模块判定结构的复杂程度,已经成为评估软件质量的一个重要标准,能帮助开发者识别难于测试和维护的模块,在成本、进度和性能之间寻求平衡。圈复杂度可以使用pmd工具来自动化计算。)
(2)我认为没有bug的软件不一定是好软件,好的软件bug数一定是尽量少的。由第一个问题的解释也可以看出,bug的确是软件工程中重要的一个方面,但是不能只由这一个方面来衡量。
- 我的看法:
- 第2章
“单元测试必须由最熟悉代码的人(程序的作者)来写”
问题:
(1)代码开发人员应该先开发代码还是先写单元测试?
(2)代码和单元测试都由同一个人编写的话,他会不会习惯性的往理想的方向编写测试代码而导致单元测试没有起到应有的作用,规避了可能出现的错误?- 我的看法:
(1)我的第一想法是要先写开发代码,觉得没有代码就不知道测试的对象,没有具体的对象不知道测试从何写起,但又觉得如果代码都写好了,在测试的过程中可能会不自觉的规避掉可能出现的问题。在自己的思维里觉得测试是通过的,但其实是存在问题的。带着这样的疑惑,我查了百度,得到的大部分答案都是说应该先写单元测试。对于没有对象怎么写单元测试这个问题,给出的解决方案是:我们可以通过先画流程图,写伪代码或者建模来解决这个问题,这样让我们站在用户的角色去开发,尽早的发现问题。
(2)我同样也认为写单元测试的人一定要足够熟悉代码,但是也有了上面的疑问。我觉得平时我们敲代码的不足之处有一部分就体现在没有考虑到很多极端或者不易想到的情况,如果是同一个人写单元测试的话,可能仍然在测试的时候,没有选用这些极端的情况或没想到的情况,而得出错误的结论。我觉得专业的测试人员可能有更好的测试思想,更好的保证用例的覆盖。但他们又不够熟悉代码。感觉各有优缺点,这也是我比较纠结的一个问题。
- 我的看法:
- PSP流程的掌握如图1:
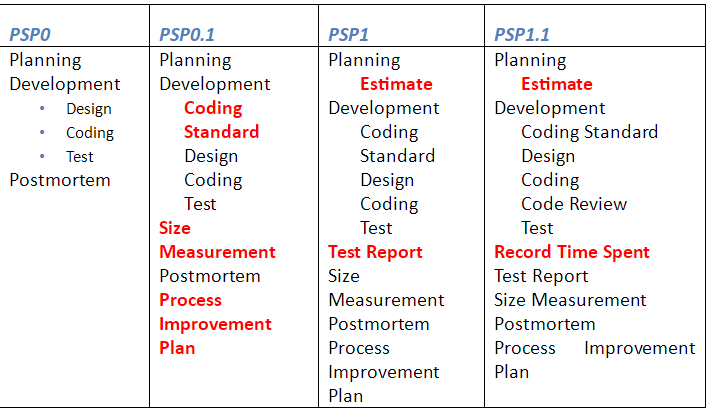
图1
任务3:项目开发背景:背包问题(Knapsack Problem,KP)是NP Complete问题,也是一个经典的组合优化问题,有着广泛而重要的应用背景。{0-1}背包问题({0-1 }Knapsack Problem,{0-1}KP)是最基本的KP问题形式,它的一般描述为:从若干具有价值系数与重量系数的物品(或项)中,选择若干个装入一个具有载重限制的背包,如何选择才能使装入物品的重量系数之和在不超过背包载重前提下价值系数之和达到最大?
D{0-1} KP 是经典{ 0-1}背包问题的一个拓展形式,用以对实际商业活动中折扣销售、捆绑销售等现象进行最优化求解,达到获利最大化。D{0-1}KP数据集由一组项集组成,每个项集有3项物品可供背包装入选择,其中第三项价值是前两项之和,第三项的重量小于其他两项之和,算法求解过程中,如果选择了某个项集,则需要确定选择项集的哪个物品,每个项集的三个项中至多有一个可以被选择装入背包,D{0-1} KP问题要求计算在不超过背包载重量 的条件下,从给定的一组项集中选择满足要求装入背包的项,使得装入背包所有项的价值系数之和达到最大;D{0-1}KP instances数据集是研究D{0-1}背包问题时,用于评测和观察设计算法性能的标准数据集;动态规划算法、回溯算法是求解D{0-1}背包问题的经典算法。查阅相关资料,设计一个采用动态规划算法、回溯算法求解D{0-1}背包问题的程序。
-
1.需求分析:
- 动态规划的核心思想避免重复计算在01背包问题中体现得淋漓尽致。第i件物品装入或者不装入而获得的最大价值完全可以由前面i-1件物品的最大价值决定,暴力枚举忽略了这个事实。
- 回溯算法:“回朔法”有通用的解题方法之称。使用它可以系统搜索一个问题的所有解或者一个解。回溯法是一个即带有系统性有带有跳跃性的算法。它在问题的解空间树中,按照深度优先的策略,从根节点出发搜索解空间树。算法搜索到解空间的任意一点时先判断该点是否包含问题的解,如果肯定不包含,就跳过对以该节点为根的子树的搜索,逐层向其祖先节点回溯。否则,进入该子树,继续按照深度优先策略搜索。回朔法求问题,要回溯到根,并且根节点的所有子树都要遍历完才结束。
-
2.功能设计:
- (1)可正确读入实验数据文件的有效D{0-1}KP数据;
- (2)能够绘制任意一组D{0-1}KP数据以重量为横轴、价值为纵轴的数据散点图;
- (3)能够对一组D{0-1}KP数据按项集第三项的价值:重量比进行非递增排序;
- (4)用户能够自主选择动态规划算法、回溯算法求解指定D{0-1} KP数据的最优解和求解时间(以秒为单位);
- (5)任意一组D{0-1} KP数据的最优解、求解时间和解向量可保存为txt文件或导出EXCEL文件。
-
3.展示PSP
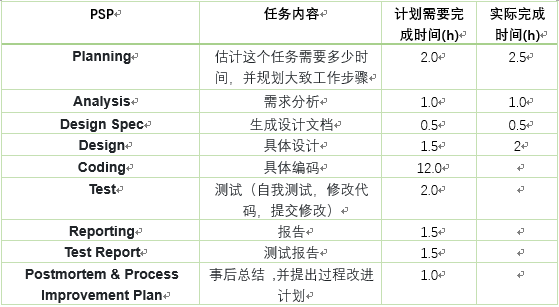
-
4.动态规划算法部分代码展示:
public static String ZeroOnePack(int V,int N,int[] weight,int[] value){ //初始化动态规划数组 int[][] dp = new int[N+1][V+1]; //为了便于理解,将dp[i][0]和dp[0][j]均置为0,从1开始计算 for(int i=1;i<N+1;i++){ for(int j=1;j<V+1;j++){ //如果第i件物品的重量大于背包容量j,则不装入背包 //由于weight和value数组下标都是从0开始,故注意第i个物品的重量为weight[i-1],价值为value[i-1] if(weight[i-1] > j) dp[i][j] = dp[i-1][j]; else dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j-weight[i-1]]+value[i-1]); } } int maxValue = dp[N][V];
任务4:完成任务3的程序开发,将项目源码的完整工程文件提交到你注册Github账号的项目仓库中。
总结
- 通过对要求中《构建之法》的阅读学习对软件、软件过程有了一些了解,着重的了解了PSP过程,对整个软件开发过程有了一定的计划之后,实行起来才更顺畅。
- 由于编程能力实在是太差差,所以本次任务完成过程较为艰难,并且完成度不高,我只能说我尽力了。