蚂蚁相遇问题

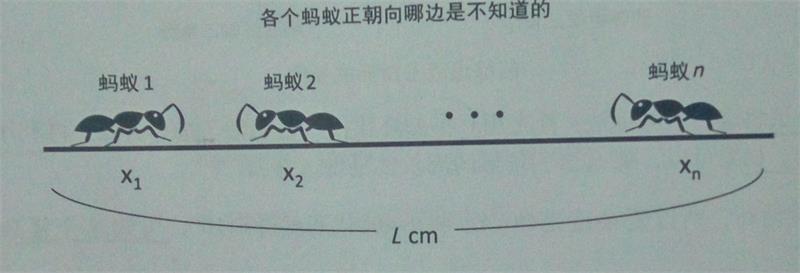
问题描述：

n只蚂蚁以每秒1cm的速度在长为Lcm的竹竿上爬行。当蚂蚁看到竿子的端点时就会落下来。由于竿子太细，两只蚂蚁相遇时，它们不能交错通过，只能各自反方向爬行。对于每只蚂蚁，我们只知道它离竿子最左端的距离为xi，但不知道它当前的朝向。请计算所有蚂蚁落下竿子的最短时间和最长时间。

                                      

限制条件：

1<=L<=106

1<=n<=106

0<=xi<=L

样例：

输入

L=10

n=3

x={2,6,7}

输出

min=4{左、右、右}

max=8{右、右、右}

其实拿到这道题目，我是懵逼的，只知道距离，蚂蚁的朝向完全不知道，就算知道，如果详细计算每一只蚂蚁和其他蚂蚁相遇后原路返回的这种情况，也是非常庞大的计算量。就拿计算蚂蚁的朝向的组合情况来说，每只蚂蚁独立的拥有两种朝向，左和右，那么n只蚂蚁的朝向组合就有2^n中情况，在这种情况下再一个个计算出每种组合下每只蚂蚁的时间，那么将会是繁杂。所以暴力求解的方法肯定是行不通的。

其实对于最短时间仔细想一下，如果每只蚂蚁一开始就向着距离自己最近的竿子那一端爬，具体来说，在坐标0~L/2之间的蚂蚁朝着左端爬，L/2~L之间的蚂蚁朝着右端爬，那么蚂蚁之间就不会相遇(因为蚂蚁的速度是一样的)。为啥这种情况下就是最短的时间？因为每一只蚂蚁的时间对于自己来说都是最小的，因为是直接朝着自己的方向走的，没有返回也没有相遇，所以在所有蚂蚁都处于自己最短的时间中只需要取出用时最长的那一个时间作为最终整体的最短用时即可。

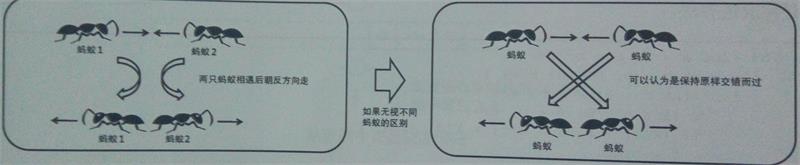
至于最长时间，那么我们就不得不考虑相遇了，因为只有不断相遇，不断折返，才能增加蚂蚁的爬行时间，那么这种情况下我们是否真的要根据每只蚂蚁的折返情况来计算时间，答案是否定的。大家可以看看下面这张图：
 

如果我们真的考虑蚂蚁在相遇后返回，那么就是上面的左图，这样的话每只蚂蚁身份都是确定的，但是如果我们不考虑蚂蚁的身份，将所有蚂蚁都视作相同无差别的，那么如上面右图所示，相当于左图中的蚂蚁1变成了蚂蚁2,蚂蚁2变成了蚂蚁1，这样的话，就可以看做蚂蚁其实并没有返回，而是"擦身而过"。我们这样想的，就会发现每只蚂蚁不断变身，那么就相当于每只蚂蚁是独立运动的，每次遇到别的蚂蚁后，就是变身一次而已，并不会影响其运动方向与轨迹。这样的话，就很简单了，求整体最长时间，就只需要求每只蚂蚁最长使用的情况下的最大值即可。
 

具体的解题代码如下:

#include<iostream>
#include<cstdlib>
#include<algorithm>
using namespace std;
int main()
{
	int L,n;
	double pos;
	cin>>L>>n;
	double minT=0,maxT=0;
	for(int i=0;i<n;i++)
	{
		cin>>pos;
		double temp=min(pos,L-pos);
		minT=max(minT,temp);
		
		temp=max(pos,L-pos);
		maxT=max(maxT,temp);
	}
	cout<<"min="<<minT<<endl;
	cout<<"max="<<maxT<<endl;
	return 0;
}

算法复杂度：

    时间复杂度O(n)

转载自：https://blog.csdn.net/qzq2514/article/details/54780882