平衡二叉搜索树(AVL)
特性:
(1)左右子树的深度之差不超过1
红黑树(RBT)
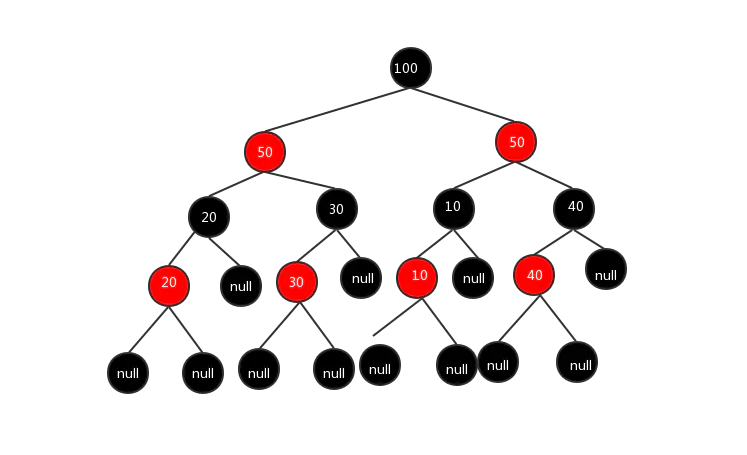
红黑树的由来,解决了什么问题:
为了维持二叉搜索树的平衡性(避免元素一边倒,变成链表),数据结构内出现了各种类型的树,如AVL树(即平衡搜索树,特性是维持左右子树的高度差不超过1)
而红黑树使用了颜色的概念维持树的平衡,使得二叉搜索树的左右子树的高度差保持在固定的范围
红黑树与AVL树对比:
由于AVL是非常严格的平衡树,导致在增删节点的时候,根据不同的情况,旋转次数比红黑树多;
红黑树是弱平衡树,因此非严格的平衡会换取增删节点时,旋转次数的减少;
总结:
若搜索次数远大于插入和删除节点的次数,选择AVL树;
若搜索次数与插入和删除节点次数差不多,选择红黑树;
本质:
一棵二叉搜索树,满足二叉搜索树的特征(即任意节点的值大于它得左子节点,小于它的右子节点)
特征:
- 根节点必须是黑色;
- 相同的红色不能相连,红色的节点,它的叶节点(NULL节点)只能是黑色;
- 从任一个节点,到其每个叶子的所有路径,都包含相同数目的黑节点;
为了保持平衡,不退化成链表,有几种方式操作
- 变颜色
- 左旋
- 右旋
B-树
定义:
一种平衡多路搜索树(并不是二叉)
特征:
【1】根节点至少有两个子女。
【2】每个中间节点都包含K-1个元素和K个孩子,其中 m/2<=k<=m
【3】每个叶子节点都包含k-1个元素,其中 m/2<=k<=m
【4】所有的叶子节点都位于同一层
【5】每个节点中的元素从小到大排列,节点当中k-1个元素正好是k个孩子包含的元素的值域分划
由来:
从算法逻辑来说,二叉查找树的查找速度和比较次数都是最小的,为什么还需要衍生出B-树的概念?
原因:考虑到磁盘IO的效率,数据库索引是存储在磁盘上的,当数据量比较大的时候,索引的大小甚至有几个G,当利用索引查询时,将整个索引加载到内存中,消耗是非常大的,
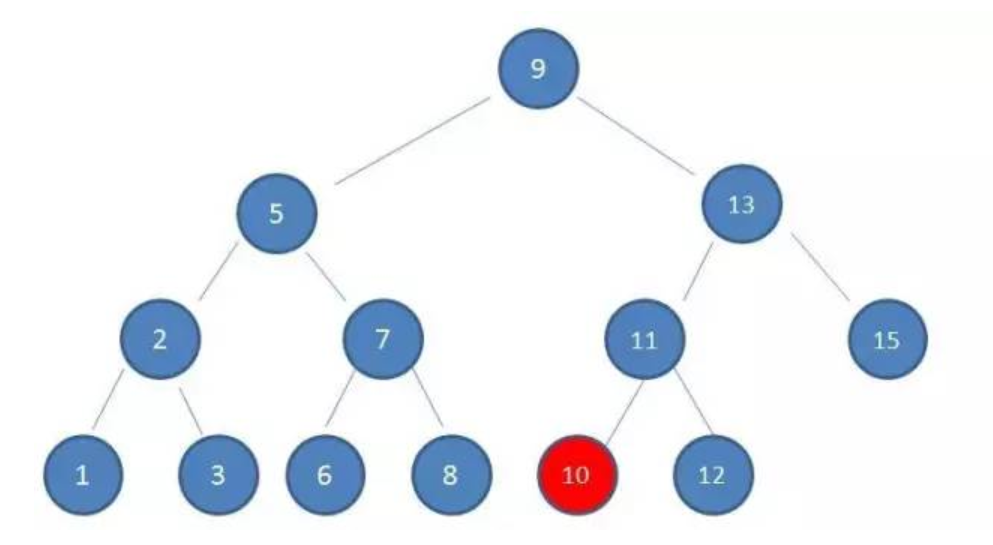
举例:用二叉查找树,查找元素10,查找的次数是4(9->13->11->10)所以最坏的情况下,磁盘IO次数等于索引树的高度。
总结:为了减少磁盘IO次数,需将搜索树由“瘦高”->“矮胖"的转变
二叉查找树:
B - 树
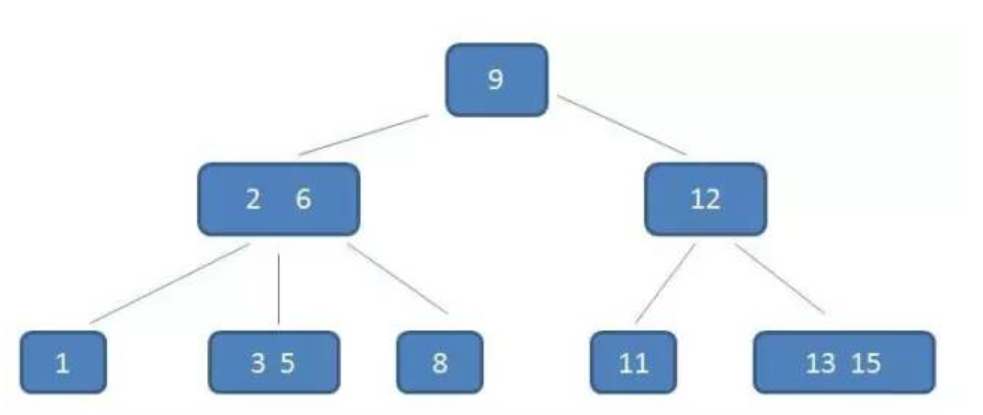
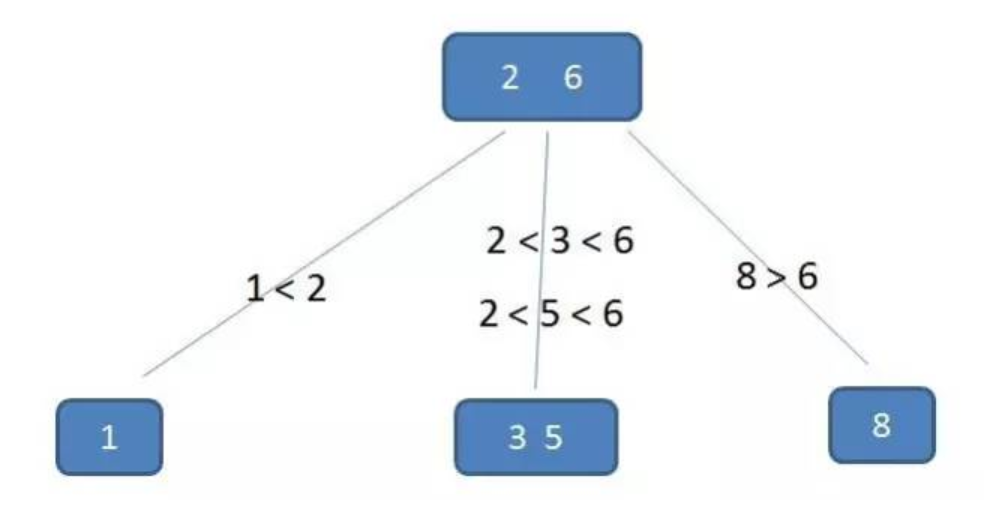
B+树
定义:
B+树是B-树的一种变体,查询性能比B-树更高
B-树 可参考
https://www.sohu.com/a/154640931_478315
https://www.cnblogs.com/linhaostudy/archive/2019/09/10/11497320.html