1.简介
gbdt全称梯度下降树,在传统机器学习算法里面是对真实分布拟合的最好的几种算法之一。
好处:
- 效果好;
- 可分类,也可回归;
- 可以筛选特征;
面试考核点:
- gbdt 的算法的流程?
- gbdt 如何选择特征 ?
- gbdt 如何构建特征 ?
- gbdt 如何用于分类?
- gbdt 通过什么方式减少误差 ?
- gbdt的效果相比于传统的LR,SVM效果为什么好一些 ?
- gbdt 如何加速训练?
- gbdt的参数有哪些,如何调参 ?
- gbdt 实战当中遇到的一些问题 ?
- gbdt的优缺点 ?
2. 正式介绍
首先gbdt 是通过采用加法模型(即基函数的线性组合),以及不断减小训练过程产生的残差来达到将数据分类或者回归的算法。
- gbdt的训练过程

gbdt通过多轮迭代,每轮迭代产生一个弱分类器,每个分类器在上一轮分类器的残差基础上进行训练。
对弱分类器的要求一般是足够简单,并且是低方差和高偏差的。因为训练的过程是通过降低偏差来不断提高最终分类器的精度,(此处是可以证明的)。
弱分类器一般会选择为CART TREE(也就是分类回归树)。由于上述高偏差和简单的要求 每个分类回归树的深度不会很深。最终的总分类器 是将每轮训练得到的弱分类器加权求和得到的(也就是加法模型)。
如果我们选择平方损失函数,那么这个差值其实就是我们平常所说的残差。
但是其实我们真正关注的:
- 1.是希望损失函数能够不断的减小
- 2.是希望损失函数能够尽可能快的减小。
所以如何尽可能快的减小呢?
- 让损失函数沿着梯度方向的下降。这个就是gbdt 的 gb的核心了。
- 损失函数负梯度在当前模型的值,作为残差的近似值曲拟合一个回归树。
- gbdt 每轮迭代的时候,都去拟合损失函数在当前模型下的负梯度。
- 这样每轮训练的时候都能够让损失函数尽可能快的减小,尽快的收敛达到局部最优解或者全局最优解。
gbdt如何选择特征?
gbdt选择特征的细节其实是想问你CART Tree生成的过程。这里有一个前提,gbdt的弱分类器默认选择的是CART TREE。其实也可以选择其他弱分类器的,选择的前提是低方差和高偏差。
在这里,我们先遍历训练样本的所有的特征,对于特征 j,我们遍历特征 j 所有特征值的切分点 c。找到可以让下面这个式子最小的特征 j 以及切分点c.

gbdt 如何构建特征 ?
其实说gbdt 能够构建特征并非很准确,gbdt 本身是不能产生特征的,但是我们可以利用gbdt去产生特征的组合。
逻辑回归本身是适合处理线性可分的数据,如果我们想让逻辑回归处理非线性的数据,其中一种方式便是组合不同特征,增强逻辑回归对非线性分布的拟合能力。
长久以来,我们都是通过人工的先验知识或者实验来获得有效的组合特征,但是很多时候,使用人工经验知识来组合特征过于耗费人力,造成了机器学习当中一个很奇特的现象:有多少人工就有多少智能。关键是这样通过人工去组合特征并不一定能够提升模型的效果。所以我们的从业者或者学界一直都有一个趋势便是通过算法自动,高效的寻找到有效的特征组合。Facebook 在2014年 发表的一篇论文便是这种尝试下的产物,利用gbdt去产生有效的特征组合,以便用于逻辑回归的训练,提升模型最终的效果。
如图 2所示,我们 使用 GBDT 生成了两棵树,两颗树一共有五个叶子节点。我们将样本 X 输入到两颗树当中去,样本X 落在了第一棵树的第二个叶子节点,第二颗树的第一个叶子节点,于是我们便可以依次构建一个五纬的特征向量,每一个纬度代表了一个叶子节点,样本落在这个叶子节点上面的话那么值为1,没有落在该叶子节点的话,那么值为 0.
于是对于该样本,我们可以得到一个向量[0,1,0,1,0] 作为该样本的组合特征,和原来的特征一起输入到逻辑回归当中进行训练。实验证明这样会得到比较显著的效果提升。
GBDT 如何用于分类 ?
首先明确一点,gbdt 无论用于分类还是回归一直都是使用的CART 回归树。
这里面的核心是因为gbdt 每轮的训练是在上一轮的训练的残差基础之上进行训练的。
这里的残差就是当前模型的负梯度值 。
 3 总结
3 总结
目前,我们总结了 gbdt 的算法的流程,gbdt如何选择特征,如何产生特征的组合,以及gbdt 如何用于分类,这个目前可以认为是gbdt 最经常问到的四个部分。至于剩余的问题,因为篇幅的问题,我们准备再开一个篇幅来进行总结。.
损失函数
只有是平方差损失函数的时候,计算得到的梯度正好是残差。
分类:
(1)指数损失函数

(2)对数损失函数
回归:
(1)均方差
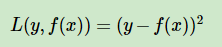
(2)绝对损失

对应的负梯度误差:
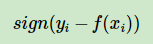
优缺点:
灵活处理各种类型的数据,包括连续值和离散值。
调参数减少,准确率高
使用一些健壮的损失函数,对异常值的鲁棒性强。
缺点:
弱分类器之间存在依赖关系,不能并行训练数据
