1.sigmod函数
[sigma(x)=frac{1}{1+e^{-x}}
]
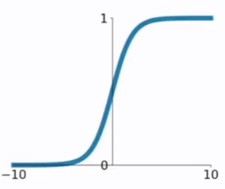
sigmod函数的输出值再(0,1)这个开区间中,经常被用来映射为概率值。
sigmod函数作为激活函数曾经比较流行。
缺陷
- 当输入稍微远离了坐标原点,函数的梯度就变得很小了,几乎为零。当反向传播经过了sigmod函数,这个链条上的微分就很小很小了,况且还可能经过很多个sigmod函数,最后会导致权重w对损失函数几乎没影响,这样不利于权重的优化,这个问题叫做梯度饱和,也可以叫梯度弥散。
- 函数输出不是以0为中心的,这样会使权重更新效率降低
- sigmod函数要进行指数运算,这个对于计算机来说是比较慢的。
tf.sigmoid(x, name=None)
2.tanh函数
[双曲正弦函数= anh(x)=frac{sinh(x)}{cosh(x)}=frac{e^x-e^{-x}}{e^x+e^{-x}}
]
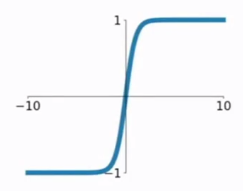
sigmod函数的输出值在(-1,1)这个开区间中,而且整个函数是以0为中心的,这个特点比sigmod的好。
缺陷
- 当输入稍微远离了坐标原点,函数的梯度就变得很小了,几乎为零。当反向传播经过了sigmod函数,这个链条上的微分就很小很小了,况且还可能经过很多个sigmod函数,最后会导致权重w对损失函数几乎没影响,这样不利于权重的优化,这个问题叫做梯度饱和,也可以叫梯度弥散。
- sigmod函数要进行指数运算,这个对于计算机来说是比较慢的。
一般二分类问题中,隐藏层用tanh函数,输出层用sigmod函数
tf.tanh(x, name=None)
3.ReLU函数
[sigma(x)=,max(0,x)
]
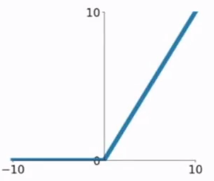
ReLU(Rectified Linear Unit)函数是目前比较火的一个激活函数
1.输入为正数的时候,不存在梯度饱和问题。
2.不存在指数运算,计算速度要快很多
缺陷
- 当输入是负数的时候,ReLU是完全不被激活的,这就表明一旦输入到了负数,ReLU就会死掉
- ReLU函数也不是以0为中心的函数
tf.nn.relu(
features,
name=None
)
4.ELU函数
[f(x)=egin{cases}
x &x>0 \ alpha(e^x-1) &x<=0
end{cases}
]
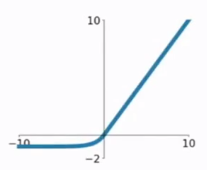
相比于ReLU函数,在输入为负数的情况下,是有一定的输出的,而且这部分输出还具有一定的抗干扰能力。这样可以消除ReLU死掉的问题,不过还是有梯度饱和和指数运算的问题。
tf.nn.elu(features, name=None)
5.PReLU函数
[f(x)=max(ax,x)
]
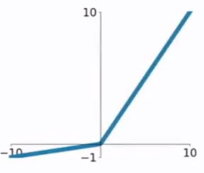
PReLU也是针对ReLU的一个改进型,在负数区域内,PReLU有一个很小的斜率,这样也可以避免ReLU死掉的问题。相比于ELU,PReLU在负数区域内是线性运算,斜率虽然小,但是不会趋于0,这算是一定的优势吧。
我们看PReLU的公式,里面的参数α一般是取0~1之间的数,而且一般还是比较小的,如零点零几。当α=0.01时,我们叫PReLU为Leaky ReLU,算是PReLU的一种特殊情况吧。