lc0329

目录

• ✅ 812. 最大三角形面积
• 描述
• 解答
  • ref
  • c
  • py

✅ 812. 最大三角形面积

https://leetcode-cn.com/problems/largest-triangle-area

描述

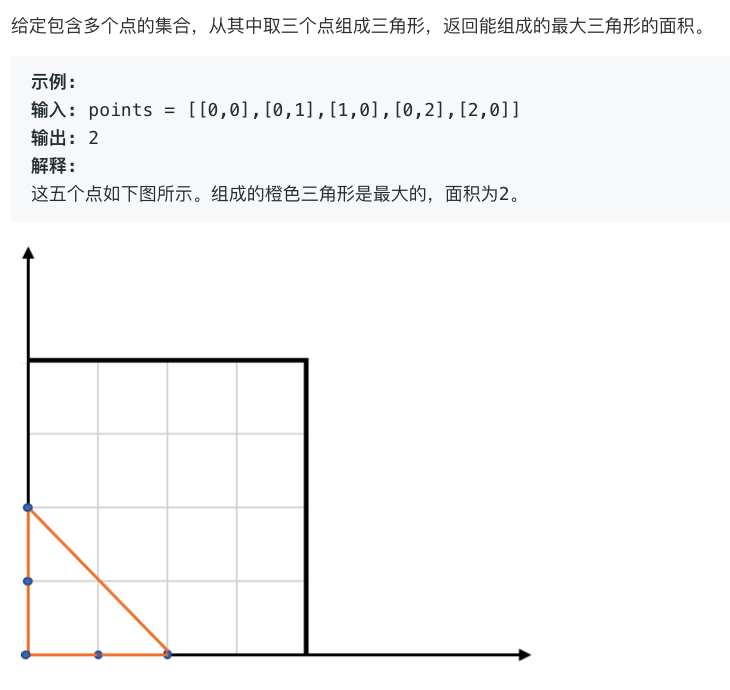
注意:

3 <= points.length <= 50.
不存在重复的点。
 -50 <= points[i][j] <= 50.
结果误差值在 10^-6 以内都认为是正确答案。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/largest-triangle-area
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解答

所以这tm是在学数学吗

三层循环加海伦公式

通过行列式去求平行四边形的面积，然后再把平行四边形的面积除以2，得到三角形面积*/
行列式和平行四边形的面积关系，证明如下

//思路：层次遍历求解，利用三点求解三角形面积的公式
//公式（x1,y1）、（x2,y2）、（x3,y3）：area=1/2|(x1y2+x2y3+x3y1-x1y3-x2y1-x3y2)|
这就是 shoelace

ref

https://bafybeiemxf5abjwjbikoz4mc3a3dla6ual3jsgpdr4cjr3oz3evfyavhwq.ipfs.dweb.link/wiki/Shoelace_formula.html

c

class Solution {
public:
    double largestTriangleArea(vector<vector<int>>& points) 
    {
        int size_1=points.size();  //有多少个坐标点
        vector<float> nums;
        float max=0;
        for(int i=0;i<size_1-2;i++)
        {
             float x1=points[i][0];
             float y1=points[i][1];
            for(int j=i+1;j<size_1-1;j++)
            {
                float x2=points[j][0];
                float y2=points[j][1];
                for(int k=j+1;k<size_1;k++)
                {
                    float x3=points[k][0];
                    float y3=points[k][1];
                    float sum=0.5*abs((x1*y2+x2*y3+x3*y1-x1*y3-x2*y1-x3*y2)); //一定别忘了取绝对值
                    if(sum>max) max=sum;
                }
            }
           
        }
        return max;
    }            
};

/*
执行用时 :
8 ms
, 在所有 C++ 提交中击败了
78.22%
的用户
内存消耗 :
7.4 MB
, 在所有 C++ 提交中击败了
100.00%
的用户
*/

py

class Solution:
    def largestTriangleArea(self, points: List[List[int]]) -> float:
        from itertools import combinations
        amax=0
        for i in combinations(points,3):
            x = [i[0][0], i[1][0], i[2][0]]
            y = [i[0][1], i[1][1], i[2][1]]
            s = abs((x[0]-x[2])*(y[1]-y[2])-(x[1]-x[2])*(y[0]-y[2]))/2
            amax=max(s,amax)
        return amax