得分情况
预估得分:(large 100 + 10 sim 100 + 20 = 130 sim 220)
实际得分:(large 40 + 10 + 20 = 70)
考场上
先看 T1,感觉是个构造题,看了一会有点烦,不看了。
再看 T2,感觉是道图论题好像是我不会的算法。
然后看 T3,字符串题,写了个超级大暴力。
回头看 T1,大概找了 1h 多的规律,觉得很对。结果很明显的 sb 错误没发现/kk
然后看 T2,大概还有 30min 多点,发现根据题意能分析出很多有用的特性,没来得及仔细分析,写了个感觉可能是正解的部分分。
T1 方
构造题。
由题目可知,当 (n = 6) 或者 (n = 9) 的时候图示的方法最优。

那么 (n = 7) 的时候一定是边长为 (3) 的正六边形最优。
考虑往边长为 (3) 的正六边形里加数,需要像下图中那样做。
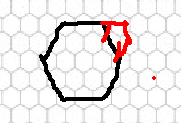
断掉两条黑色的边,连三条红色的边。
考虑边长大于 (3) 的一条边。
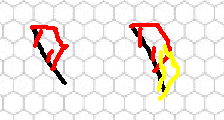
断了两条边并连了三条边之后会出现一种特殊情况,断两条边再连两条边。且边越长这样的特殊情况越多,如果边长为 (l) 那么我们只需要使周长加 (1) 就能够多加 (l - 2) 个点。
按照上述方法对一条边进行操作会使得被操作的边减 (1),与被操作的边相邻的边加 (1),每次找最长边操作。
并且存在一种类似循环节的感觉,如下图(代码中的 (times) 表示这种循环)。

Code:
#include <cstdio>
#include <cstring>
#include <string>
#include <iostream>
#include <algorithm>
int n, f[17];
int main() {
f[1] = 6, f[2] = 8, f[3] = 9, f[4] = 10, f[5] = 11, f[6] = 12, f[7] = 12;
std::cin >> n;
if (n < 7) std::cout << f[n] << '
';
else {
int ans = f[7]; n -= 7;
int bian = 3, times = 2;
while (n > 0) {
if (times == 1) n -= bian - 1;
if (times == 2) n -= bian - 2;
if (times > 2 && times <= 6) n -= bian - 1;
ans += 1;
++times;
if (times == 7) { times = 1, ++bian; }
}
std::cout << ans << '
';
}
fclose(stdin), fclose(stdout);
return 0;
}
T2
如果按 (u) 可以买到 (v) 就连一条 (u ightarrow v) 的边,最后会有 (n) 条边。
有三种情况:
-
只有自环收益不为负数就全选。
-
只有个环环上如果有负的收益就把正的收益加起来,如果没有负的收益还要减去一个单个的收益的最小值。
-
有个环,还有别的连向环的边
分类讨论来计算即可。代码好难写,没写出来/kk
T3 油炸字符串
dp。